Наиболее распространенными законами распределения НСВ являются следующие:
1. Равномерное распределение.
 НСВ Х, принимающая значение на отрезке [a,b], имеет равномерное распределение, если плотность распределения:
НСВ Х, принимающая значение на отрезке [a,b], имеет равномерное распределение, если плотность распределения:
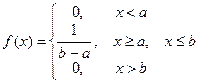 .
.
Для СВ, имеющей равномерное распределение, вероятность того, что она примет значение в интервале (х, х +  х)
х) 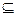 [a,b] не зависит от положения интервала на числовой оси и пропорциональна длине этого интервала (
[a,b] не зависит от положения интервала на числовой оси и пропорциональна длине этого интервала (  ).
).
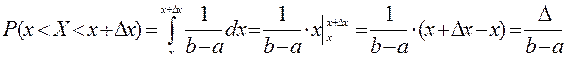 .
.
Функция распределения равномерно распределенной СВ имеет вид:

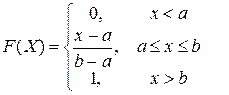
Можно показать, что М(Х) равномерно распределенной СВ имеет вид:
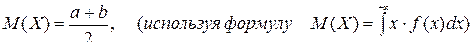 .
.
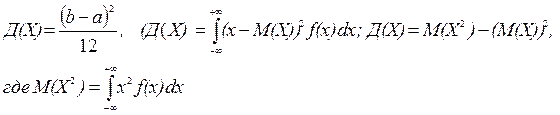
Например: автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Найти вероятность того, что пассажир на остановке будет ждать автобус менее трех минут.
Время ожидания автобуса – СВ Х; СВ Х распределена равномерно, в интервале (0,5).
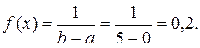
Определим вероятность попадания СВ в (0  Х<3):
Х<3):
Р(0  Х<3) =
Х<3) = 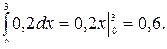
2. Показательное распределение.
НСВ Х, принимающая отрицательные значения, имеет показательное распределение с показателем λ, если плотность распределения этой СВ имеет вид:
|
|

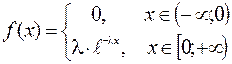

Тогда функция распределения СВ Х имеет вид:
|
|
|

|
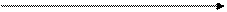


Вероятность попадания СВ Х, распределенной по показательному закону, в [a,b] определяется по формуле:
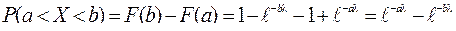
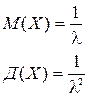
Показательное распределение часто встречается в теории массового обслуживания и в теории надежности.
3. Нормальное распределение.
НСВ Х имеет нормальное распределение вероятностей с параметрами а и σ>0, если ее плотность распределения имеет вид:
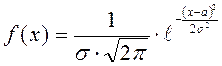
Если НСВ Х имеет нормальное распределение, то это записывается в виде:
N(a; σ).
Чтобы выяснить смысл параметров а и σ , входящих в выражение плотности распределения, достаточно найти М(Х) и Д(Х) нормально распределенной СВ Х.
а = М(Х) = 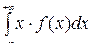
σ = 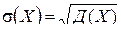 , где Д(Х) =
, где Д(Х) = 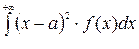 .
.

Если провести полное исследование функции f(x) с использованием дифференциального исчисления, то можно построить график функции распределения нормально распределенной НСВ Х. этот график будет называться кривой Гаусса.
Свойства функции f(x):
1. функция f(x) неотрицательная;
2. f(x)→0, если х 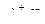 ;
;
3. f(x) симметрична относительно х = а;
4. 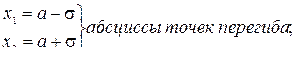
5. если изменять а (σ - const), то форма графика функции f(x) не меняется. Кривая лишь сдвигается по ОХ. Если а не изменять, σ изменять, то с уменьшением σ «холм» кривой становится выше и уже. Это объясняется тем, что σ – мера рассеяния. Чем меньше σ, тем плотнее значения СВ Х группируются вокруг ее среднего значения а. чем ближе значения СВ Х к среднему значению, тем больше их вероятность.
6. а = 0, σ = 1 = нормальный закон распределения называется нормированным или стандартным.
Функция распределения нормально распределенной СВ Х имеет вид:
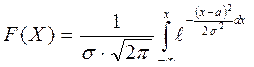
Вероятность того, что СВ Х примет значение в интервале 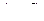 равна:
равна:
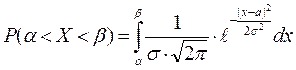 ,
,
где 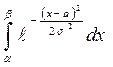 -- «неберущийся» интеграл в элементарных функциях.
-- «неберущийся» интеграл в элементарных функциях.
Этот интеграл можно вычислить приближенно. Упростить вычисление можно, если ввести функцию Лапласа:
Ф(Х) = 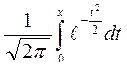
Тогда 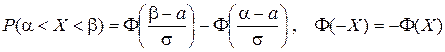 .
.
Вероятность отклонения НСВ Х от своего М(Х) определяется по формуле:
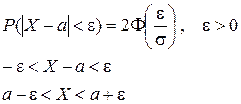
Если предположить, что ε = 3σ, то получим следующую формулу:
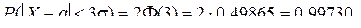
Это равенство показывает особенность нормального закона распределения. Оно утверждает, что значения СВ с очень большой вероятностью (равной 0,99730) лежат в промежутке [a - 3σ; а + 3σ].
Вероятность того, что СВ примет значение вне указанного промежутка ничтожно мала и составляет 0,0027. Этот вывод называется правилом «трех сигм»: если СВ Х распределена нормально, то модуль ее отклонения от М(Х) не превосходит трех сигм.
Практический интерес представляют вероятности попадания СВ в интервалы [a - 2σ; а + 2σ] , [a - σ; а + σ].
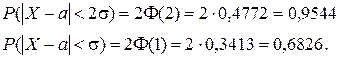
Вместо этого правила можно воспользоваться интервалами значений для обычно используемой вероятности.
Р = 0,99
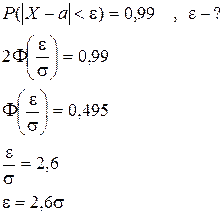
Закон больших чисел
Под законом больших чисел (ЗБЧ) понимают ряд теорем, описывающих закономерности поведения усредненных результатов большого числа n повторных испытаний, если результат каждого отдельного испытания есть случайное событие или СВ.
Смысл ЗБЧ состоит в том, что при большом числе повторных испытаний их усредненный результат практически перестает быть случайным и может быть предсказан с высокой достоверностью, т.е. с вероятностью, близкой к единице.
ЗБЧ описывается рядом теорем, при доказательстве которых используется неравенство Чебышева. Теоремы:
- теорема Чебышева
- теорема Бернулли
- теорема Ляпунова (центральная предельная теорема ТВ).
Неравенство Чебышева
Вероятность того, что отклонение СВ от ее М(Х) превзойдет по абсолютной величине положительное число ε, не больше дроби, числитель которой есть Д(Х), а знаменатель есть ε2.
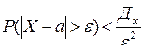 .
.
Если рассматривать противоположное событие для 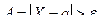 , т.е.
, т.е.
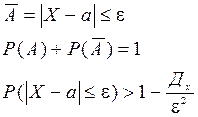
Теорема Чебышева
Пусть имеется конечная последовательность Х1, Х2,…, Хn независимых СВ с одним и тем же М(Х): М(Х1) = М(Х2) = … = М(Хn) = а. И дисперсиями, ограниченными одной и той же постоянной С: Д(Х1)  С, Д(Х2)
С, Д(Х2)  С, …, Д(Хn)
С, …, Д(Хn)  С. Тогда, каково бы ни было данное положительное число ε, вероятность события стремится к единице при n→∞.
С. Тогда, каково бы ни было данное положительное число ε, вероятность события стремится к единице при n→∞.
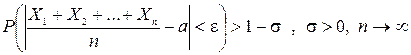 .
.
Число СВ достаточно велико. Теорема Чебышева показывает, что при достаточно большом числе измерений некоторой СВ средне арифметическое значение этих измерений приближается к М(Х).
Теорема Бернулли
Если вероятность наступления события А в каждом из n независимых испытаний постоянна, а число испытаний достаточно велико, то вероятность того, что частость события А будет как угодно мало отличаться от его вероятности сколь угодно близка к единице.
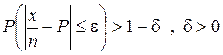 .
.
Ценность этой теоремы заключается в том, что если вероятность события А в отдельном испытании не известна, то ее можно с достаточной для практических целей точностью и надежностью принять равной относительной частоте r(A) появления этого события в длинной серии таких испытаний.
Р(А) ≈ r(A), n → ∞.
Теорема Ляпунова
Если СВ представляет собой сумму очень большого числа взаимно независимых СВ, влияние каждой из которых на всю сумму ничтожно мало, то СВ имеет распределение, близкое к нормальному.
Эта теорема имеет огромное значение для практики. Согласно ей можем ожидать, что изменчивость таких показателей, как рост и обхват груди человека, определение возраста и пола, вес отдельного яблока или булки хлеба, величина ошибки измерения некоторого физического показателя и т.д. должны хорошо описываться законом нормального распределения, что и наблюдается на практике.
Системы случайных величин
При исследовании случайных явлений часто приходится рассматривать одновременно несколько СВ. Их совокупность можно представить как многомерную СВ.
Двумерная СВ – СВ (X, Y), каждое возможное появление которой представляет собой пару чисел (x; y) случайных величин X и Y, рассматриваемые совместно.
СВ, рассматриваемые совместно, образуют систему двух СВ.
| Y | X | |||
| x1 | x2 | … | xn | |
| y1 | P(x1,y1) | P(x2,y1) | … | P(xn,y1) |
| … | … | … | … | … |
| ym | P(x1,ym) | P(x2,ym) | … | P(xn,ym) |
Двумерная СВ – дискретная.
Каждой паре значений (xi; yj) ставится в соответствие вероятность появления этой пары Р(X = хi, Y = yj).
Общей характеристикой двумерной СВ является функция распределения вероятностей, которая представляет собой вероятность события, что X<x, Y<y.
F(x, y) = P(X < x, Y < y).
Для НСВ функция распределения записывается в виде интеграла:
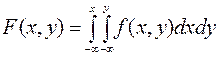 , где f(x, y) – плотность распределения вероятностей двумерной СВ.
, где f(x, y) – плотность распределения вероятностей двумерной СВ.
Вероятность совместного появления ДСВ (двумерной) записывается в виде:
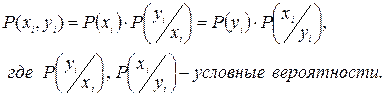
Для НСВ плотность распределения вероятностей записывается в виде:
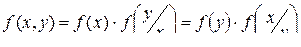 .
.
Дата: 2019-02-25, просмотров: 314.