Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

1) Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером;

2) Перестановка двух столбцов или строк определителя равносильна умножению его на -1;

3) Если определитель имеет два одинаковых столбца или строки, то он равен 0;

4) Произведение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению его на это число;

5) Если все элементы некоторого столбца или строки равны 0, то и определитель также равен 0;

6) Если соответствующие элементы двух столбцов или строк пропорциональны, то определитель равен 0;

7) Если каждый элемент n-го столбца или строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-ом столбце (строке) имеет первые слагаемые, а другой – вторые. Элементы, стоящие на остальных местах, не меняются;

8) Если к элементам некоторого столбца (строки) прибавить соответствующие элементы другого столбца (строки), умноженные на любой общий множитель, то величина определителя не изменится;

9) Определитель равен сумме произведений элементов какой-либо строки (столбца) на их соответствующие алгебраические дополнения.

Применение свойств 8 и 9 дает способ вычисления определителей любого порядка.

Свойство 9 часто называют разложением определителя по элементам какой-либо строки (столбца).

 

а₁₁ а₁₂ а₁₃ = а₁₁∙А₁₁ + а₁₂ ∙А₁₂ + а₁₃∙А₁₃

а₂₁ а₂₂ а₂₃  = а₂₁∙А₂₁ + а₂₂ ∙А₂₂ + а₂₃∙А₂₃

а₃₁ а₃₂ а₃₃  = а₃₁∙А₃₁ + а₃₂ ∙А₃₂ + а₃₃∙А₃₃

 

 

Виды матриц. Ранг матрицы

 

Любая таблица, состоящая из чисел, записанных в определенном порядке, содержащая m строк и n столбцов, называется матрицей размерности m×n; число a_ij – элемент матрицы.

Способы задания матриц:

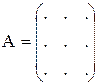
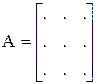
А_1×n – матрица-строка

А_1×m – матрица-столбец

 

Матрица, все элементы которой – нули – нулевая матрица.

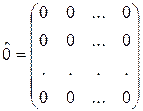
Если m≠n, матрица – прямоугольная;

если m>n, матрица – укороченная;

если m<n, матрица – удлиненная;

если m=n, матрица – квадратная.

 

|A| – определитель матрицы.

Размерность квадратной матрицы называется ее порядком.

Если определитель квадратной матрицы ≠ 0, то такая матрица – невырожденная (неособенная);

Если определитель квадратной матрицы = 0, то такая матрица – вырожденная (особенная).

Квадратная матрица вида

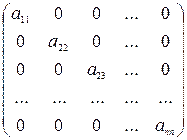
где а₁₁, а₂₂, … , а _nn – элементы , распределенные по главной диагонали, называется диагональной матрицей.

Диагональная матрица, все элементы которой по главной диагонали равны 1, называется единичной матрицей (E_n).

 

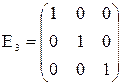
Любое число можно считать матрицей первого порядка.

Если у матрицы переставить местами столбцы со строками, то такая операция называется транспонированием матрицы.

А^т – транспонированная матрица.

|А| = |А^т| (если А – квадратная)

(А^т)^т = А

Квадратная матрица называется симметрической, если А = А^т , т.е. a_ij = a_ji для любых i и j.

Элементы симметрической матрицы, расположенные симметрично относительно главной диагонали, равны.

 

Квадратная матрица называется ортогональной, если ее столбцы образуют ортонормированную систему векторов.

 Рассмотрим матрицу А = (a_ij), i = 1, m ; j = 1, n .

Из этой матрицы можно образовать квадратные матрицы. Определители таких матриц называют минорами данной матрицы. Порядок этих миноров не превышает min(m , n).

 

Пример:

Для матрицы А_5×4 наибольший порядок минора ≤ 4.

 

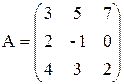 – квадратная матрица 3 порядка:

9 миноров 1 порядка;

9 миноров 2 порядка;

1 минор 3 порядка;

 

Рангом матрицы называется максимальный порядок миноров матрицы, отличных от нуля.

Если ранг матрицы r(A) = r, то по крайней мере один из миноров этой матрицы порядка r отличен от нуля, и все миноры более высоки порядков (если они существуют) равны 0.

 

Ранг матрицы можно вычислить следующими методами:

1) Метод окаймляющих миноров

2) Метод, основанный на элементарных преобразованиях матрицы

 

Рассмотрим первый метод.

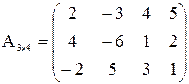
r(A) может принимать значения 1, 2, 3.

Выбираем минор первого порядка:

М₁ = -3

Составляем М₂, окаймляющий М₁ ≠ 0

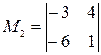 = 21 ≠ 0

=> r(A) = 2 или 3.

Составляем М₃, окаймляющий М₂ 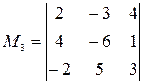≠ 0

 ≠ 0

=> r(A) = 3

 

Базисным минором матрицы называется минор, не равный нулю, порядок которого равен рангу данной матрицы.

 

Действий с матрицами

 

1) Сумма матриц

Складывать можно только матрицы с одинаковым числом строк и столбцов. Суммой матриц А = (a_ij) и В = (b_ij) называется новая матрица С = (с _ij), элементы которой равны суммам соответствующих элементов матриц А и В.

с _ij = a_ij + b_ij

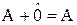
Операции сложения матриц обладают свойствами коммутативности, ассоциативности и дистрибутивности.

2) Умножение матрицы на число

Произведением матрицы А = (a_ij) на число k называется новая матрица, элементы которой равны произведениям соответствующих элементов матрицы А на число k.

А ∙ k = (k ∙ a_ij)

k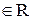

А ∙ k = k ∙ А

 

3) Умножение матриц

Произведение матрицы А на матрицу В определено только в том случае, когда число столбцов матрицы А равно числу строк матрицы В.

В результате умножения получаем матрицу, у которой столько же строк, сколько у первой матрицы и столько же столбцов, сколько у второй.

А ∙ В ≠ В ∙ А

A_{m × n} ∙ B_{n × k} = C_{m × k}

Если произведение матриц возможно, то матрицы А и В называют сцепленными.

Чтобы получить элементы новой матрицы, надо составить сумму произведений элементов какой-либо строки матрицы А на соответствующие элементы какого-либо столбца матрицы В.

 

с _ij = a_{i 1} ∙ b _{1 j} + a_{i 2} ∙ b _{2 j} + … + a_in ∙ b_nj

 

Если А ∙ В = В ∙ А, то матрицы А и В называются перестановочными.

 

Обратная матрица

 

Обратная матрица может существовать только для квадратных матриц. Не каждая квадратная матрица имеет обратную матрицу. Если квадратная матрица – не вырожденная, она всегда имеет обратную матрицу, и при том единственную.

 Если квадратная матрица вырожденная, то для такой матрицы не существует обратной.

 

Если существует квадратная матрица В, такая, что А ∙ В = В ∙ А = Е – единичная матрица того же порядка, что и квадратные матрицы А и В, то будем говорить, что матрица А обратима, и матрицу В будем называть обратной для матрицы А.

В = А^-1

 

Справедливы следующие утверждения:

1) Каждая невырожденная матрица обратима;

2) Матрица обратима тогда и только тогда, когда она невырожденная;

3) Обратимая матрица А имеет только одну обратную матрицу.

 

Нахождение обратной матрицы можно выполнять 2 методами:

1) Метод присоединенной матрицы;

2) Метод, основанный на элементарных преобразованиях матриц.

 

Рассмотрим первый метод.

Обратную матрицу можно найти по формуле:

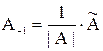
где 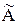– присоединенная матрица

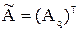
где 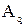 – матрица, элементами которой являются алгебраические дополнения элементов определителя исходной квадратной матрицы.

 

Пример:

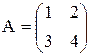
Найти А^-1

|A| = 4 ∙ 6 = -2 ≠ 0

А₁₁ = М₁₁ = 4;

А₁₂ = -М₁₂ = -3;

А₂₁ = -М₂₁ = -2;

А₂₂ = М₂₂ = 1.

 

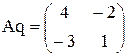
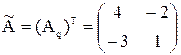
9.5 Элементарные преобразования матриц

 

Элементарные преобразования матрицы приводят к матрице, эквивалентной исходной.

А ~ В – эквивалентные матрицы.

Эквивалентные матрицы имеют одинаковые ранги.

 

К элементарным преобразованиям относят:

1) Перестановка местами любых двух столбцов (строк);

2) Умножение каждого элемента произвольного столбца (строки) на число k ≠ 0;

3) Вычеркивание столбца (строки) из нулей;

4) Прибавление к элементам произвольного столбца (строки) соответствующих элементов любого другого столбца (строки), умноженных на произвольное число, отличное от нуля.

5) Транспонирование матрицы

 

С помощью элементарных преобразований можно находить обратную матрицу:

1) Приписать справа к матрице А единичную матрицу того же порядка, что и А (А  Е);

2) Элементарными преобразованиями строк составленной матрицы за конечное число шагов привести матрицу вида (А Е) к матрице вида (Е В);

3) Получившаяся в правой половине матрица В и будет обратной матрице А,
В = А^-1;

4) Проверка: А ∙ А^-1 = Е, либо А^-1 ∙ А =Е.

 

Обратную матрицу можно находить и следующим образом:

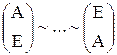
При этом работают со столбцами.

Элементарные преобразования матриц можно применять к нахождению ранга матрицы т.к. если А ~ В, то r(А) = r(В).

Матрица размера m×n вида

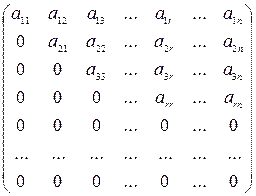
называется трапецеидальной.

а₁₁, а₂₂, а₃₃, … , а _rr ≠ 0 (отдельные могут равняться 0).

 

Каждую матрицу с помощью элементарных преобразований можно превратить в трапецеидальную. Ранг трапецеидальной матрицы равен числу ненулевых строк.

Т.к. элементарные преобразования матрицы не меняют ее ранга, то для отыскания ранга любой матрицы нужно:

1) Преобразовать данную матрицу в трапецеидальную;

2) Подсчитать число ненулевых строк

3) Ранг трапецеидальной матрицы будет равен рангу данной матрицы.