Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

8.1.1 Различные уравнения прямой на плоскости

Уравнение вида (1) F (x, y) = 0 определяет линию на плоскости, когда точки, лежащие в этой линии, удовлетворяют, а точки, не лежащие в этой прямой, не удовлетворяют ему.

 

1. Пусть прямая l имеет M₀  (x₀, y₀)

 

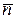
 l, где 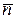– нормальный вектор прямой. Точка и вектор определяют единственную прямую на плоскости.

M(x, y) – точка с текущими координатами. Рассмотрим 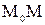 = (x - x₀, y - y₀).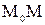  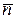=>  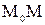∙  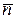= 0                                                                                     (1)

– векторное уравнение прямой.

 

Используем определение скалярного произведения и получаем:

A(x - x₀) + B(y - y₀) = 0                                                                              (2)

– уравнение прямой, проходящей через точку и  к данному вектору.

 

2.    

   

     

 

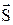 || l;  M₀  l; 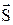   – направляющий вектор прямой l;

M(x, y)  l  

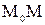 =  (x - x₀, y - y₀);  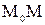  || 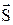 (коллинеарны);  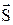= (m, n);

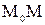 =  t ∙ 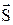,  t – параметр

 

 =                                                                                            (3)

– каноническое уравнение прямой;

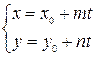
– параметрическое уравнение прямой.

 

3.

 

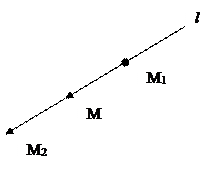M₁(x₁, y₁) 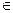 l

M₂(x₂, y₂) 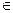 l

M₃(x₃, y₃) 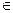 l

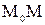 =  (x - x₁, y - y₁)

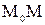 =  (x₂ - x₁, y₂ - y₁)                  

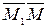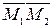 ||  – коллинеарны  

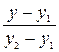 =                                                                                          (5)

– уравнение прямой, проходящей через две данные точки.

 

4. 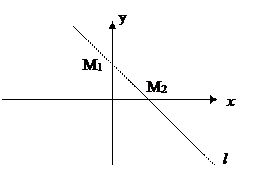Прямая l пересекает оси координат.

 

 

M₁  (0, b)     M₂ (a, 0)

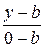
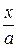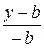
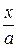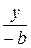 =      =    =  + 1 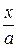 +  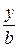 = 1                    (6)

– уравнение прямой в отрезках на осях. 

 

 ‌‌‌ ‌‌  =      

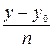
OAB – прямоугольник, OB = m   

AB = n tg  =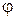

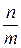
tg 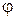 = k – угловой коэффициент прямой l 

y - y₀ = 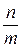 ∙ (x - x₀);  y - y₀ = k ∙ (x - x₀)                                                 (7)

L

 – уравнение прямой, проходящей через данную точку в данном направлении, если k - производная, то уравнение (7) – уравнение пучка прямых.

 

y - b = k ∙ x ;  y = k ∙ x + b                                                                   (8)

– уравнение прямой с угловым коэффициентом.  

  

 

 

A(x - x₀) + B(y - y₀) = 0 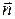 - ненулевой вектор 

A ∙ x + B ∙ y - A ∙ x_{0 -} B ∙ y₀ = 0; C = - A ∙ x₀ - B ∙ y₀; A ∙ x + B ∙ y + C = 0 (9)

– общее уравнение прямой (полное, если A 0, B 0, C 0)

 

Если уравнение прямой задано общим уравнением, то k = -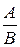  

Если известны две точки, то .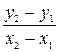 

 

8.1.2 Расстояние от точки, не лежащей на прямой, до прямой, заданной общим уравнением

 

Найти d - расстояние от M₀ до l       

d = 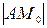 = A ∙ x₀ + B ∙ y₀ + C

 ₌

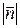8.1.3. Взаимное расположение двух прямых на плоскости.                                                                     

 

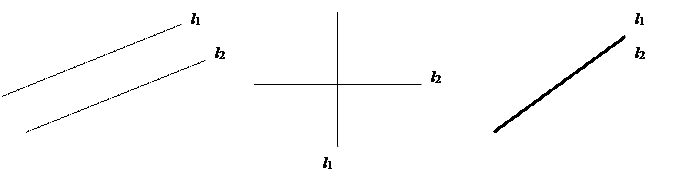
1)

l₁: y = k₁ ∙ x + b₁                          k₁ = tg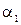  

l₂: y = k₂ ∙ x + b₂                           k₁ = tg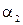

tg 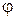 = tg (  - ) =           

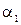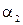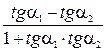
tg  =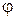    

 

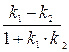
2)

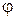 = 0    

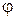tg  = 0     

k₁ = k₂ - параллельны

 

3)

tg 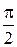 - не существует       

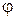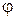tg  = ctg  = 1       

ctg  =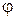       

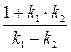
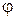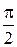 = , если l₁  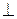l₂, то ctg  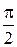= 0     

k₁ ∙ k₂ = - 1        

k₁ = - 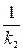   - перпендикулярны.

Рассмотрим уравнения прямых l₁, l₂, заданных общим уравнением.

l₁: A₁ ∙ x + B₁ ∙ y + C₁ = 0 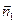      = (A₁, B₁)  l₁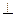   

l₂: A₂ ∙ x + B₂ ∙ y + C₂ = 0 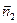      = (A₂, B₂)  l₂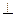

 

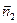
Под углом между двумя прямыми понимают угол между нормальными векторами данных прямых.

1. cos  =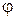     

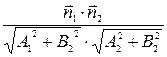
n₁ ∙ n₂ = A₁ A₂ + B₁ B₂   

 

2. l₁ || l₂ => 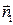 || , значит координаты нормальных векторов пропорциональны 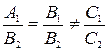 - условие параллельности        

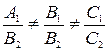 - прямые пересекаются

 

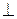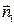
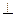
3. l₁ l₂ =>      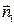  =>  ∙  = 0 => A₁ ∙ A₂ + B₁ ∙ B₂ = 0    

4. l₁ совпадает с l₂, координаты пропорциональны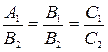  

Аналитическая геометрия в пространстве.

8.2.1. Различные уравнения плоскости.

 

         

 

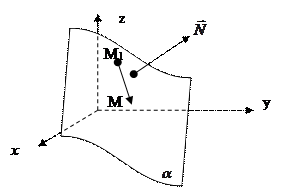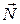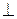
 = (A, B, C),  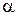                         M₁ (x₁, y₁, z₁)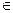 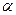               M (x, y, z)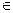

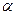
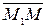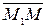
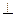
 = (x - x₁, y - y₁, z - z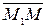₁)           ∙  = 0        (1)

– скалярное произведение  

A(x - x₁) + B(y - y₁) + C(z - z₁) = 0                                                          (2)

–уравнение плоскости, проходящей через точку M₁, перпендикулярно данному вектору.       

 

A ∙ x + B ∙ y + C ∙ z + D = 0 – общее уравнение плоскости.

 

Особые случаи (3) :

1. D = 0 A ∙ x + B ∙ y + C ∙ z = 0 – плоскость, проходящая через начало координат.

2. C = 0 A ∙ x + B ∙ y + D = 0 – плоскость параллельная оси OZ.  

3. C = D = 0 A ∙ x + B ∙ y = 0 – плоскость, проходящая через ось OZ.

4. B = C = 0 A ∙ x + D = 0 – плоскость параллельная плоскости YOZ.

5. X = 0 Y = 0 Z = 0 – уравнения координатных плоскостей.

6. A 0, B 0, C 0, D 0  

 

Преобразуем (3)  

A ∙ x + B ∙ y + C ∙ z = - D |: (-D)  

a =           b =           c =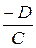

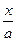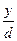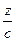 +  +  = 1 (4) – уравнение плоскости в отрезках на осях.

z