1. Пересечение двух плоскостей.
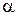 : A1 ∙ x + B1 ∙ x + C1x + D1 = 0
: A1 ∙ x + B1 ∙ x + C1x + D1 = 0
 : A2 ∙ x + B2 ∙ x + C2x + D 2 = 0
: A2 ∙ x + B2 ∙ x + C2x + D 2 = 0
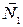 = (A1, B1, C1),
= (A1, B1, C1), 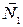
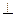
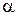
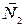 = (A2, B2, C2),
= (A2, B2, C2), 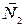

cos  =
= 
2. Условия параллельности плоскостей.
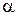 : A1 ∙ x + B1 ∙ у + C1 ∙ z + D1 = 0
: A1 ∙ x + B1 ∙ у + C1 ∙ z + D1 = 0 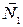 = (A1, B1, C1)
= (A1, B1, C1)
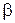 : A2 ∙ x + B2 ∙ y + C2 ∙ z + D2 = 0
: A2 ∙ x + B2 ∙ y + C2 ∙ z + D2 = 0 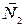 = (A2, B2, C2)
= (A2, B2, C2)
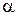 ||
|| 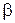 =>
=> 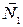 ||
||  = >
= > 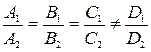
3. Условия перпендикулярности.
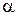
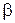 <=>
<=> 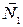
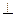
 <=> A1 ∙ A2 + B1 ∙ B2 + C1 ∙ C = 0
<=> A1 ∙ A2 + B1 ∙ B2 + C1 ∙ C = 0
4. 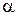 совпадает с
совпадает с 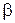
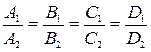
d = 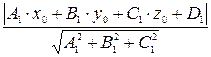
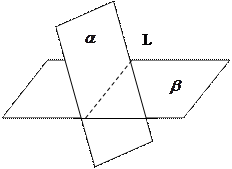
Различные уравнения прямой в пространстве.
Прямая в пространстве может быть задана двумя пересекающимися плоскостями.
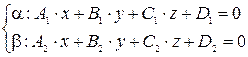 (1)
(1)
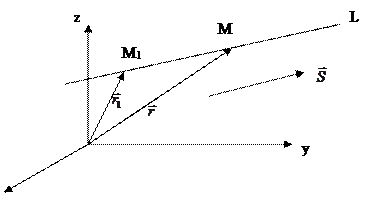 |
M1 (x1, y1, z1)  L
L
M (x, y, z)  L
L
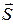 || L
|| L
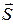 (m, n, p)
(m, n, p)
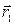 = (x1, y1, z1)
= (x1, y1, z1) 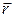 = (x, y, z)
= (x, y, z)
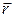 =
= 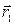 + t ∙
+ t ∙ 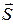 (2) - векторное уравнение прямой L в пространстве.
(2) - векторное уравнение прямой L в пространстве.
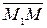 = t ∙ s
= t ∙ s 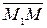 ||
|| 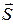 , t – параметр.
, t – параметр.
Если 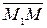 и
и 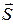 – коллинеарны, то их координаты пропорциональны
– коллинеарны, то их координаты пропорциональны
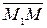 = (x - x1, y - y1, z - z1)
= (x - x1, y - y1, z - z1)
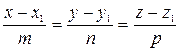 (3)
(3)
– канонические уравнения прямой в пространстве.
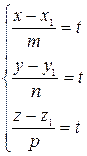 = >
= > 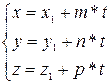 (4)
(4)
- параметрические уравнения прямой в пространстве.
 |
 =
= 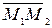
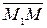 = (x - x1, y - y1, z - z1)
= (x - x1, y - y1, z - z1)
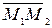 = (x2 - x, y2 - y, z2 - z)
= (x2 - x, y2 - y, z2 - z)
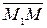 = t ∙
= t ∙ 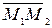
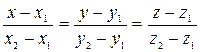 (5)
(5)
– уравнения прямой, проходящей через две заданные точк.
8.2.4 Расположение прямых в пространстве R 3
1. Угол между двумя прямыми с данными направляющими векторами.
L1: 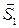 = (m1, n1, p1)
= (m1, n1, p1)
L2: 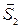 = (m2, n2, p2)
= (m2, n2, p2)
cos 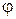 =
= 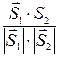
2. L1 || L2 => 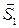 ||
|| 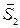 = >
= > 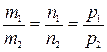
3. L1 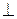 L2 =>
L2 => 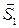
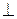
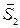 m1 ∙ m + n1 ∙ n + p1 ∙ p = 0
m1 ∙ m + n1 ∙ n + p1 ∙ p = 0
8.2.5 Прямая и плоскость в пространстве
L: 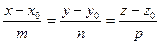 M0 (x0, y0, z0)
M0 (x0, y0, z0)  L
L 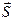 (m, n, p)
(m, n, p) 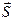 ׀׀ L
׀׀ L
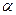 : A · x + B · у + C · z + D = 0
: A · x + B · у + C · z + D = 0 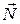 = (A, B, C)
= (A, B, C) 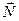
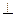
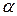
1. Угол между прямой и плоскостью 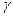 =
= 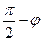 cos
cos 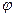 = cos(
= cos( 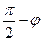 )= sin
)= sin 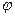
cos  =sin
=sin 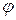 =
= 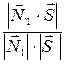 sin
sin 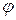 >=0
>=0
2. L1 || 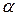 =>
=> 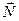
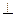
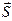 => A · m + B · n + C · p = 0
=> A · m + B · n + C · p = 0
3. L1 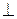
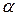 =>
=> 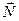 ׀׀
׀׀ 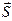 =>
=> 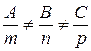
8.2.6. Определение точки пересечения прямой и плоскости
Уравнение прямой следует записать параметрическими уравнениями.
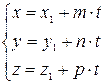 (*)
(*)
A · x+B · x + C · x + D = 0 подставить x , y , z в общее уравнение .
Найти значения параметра t и подставить в равенство (*).
1. Составить параметрические уравнения прямой, проходящей через M0 (1, -1, -3):
· параллельно вектору 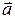 = (2, -3, 4)
= (2, -3, 4)
· параллельно прямой
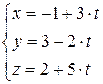
· и точку M1 (1, 1, 0)
2. Составить канонические уравнения прямой, проходящей через M0 (2, 0, -3):
· параллельно вектору 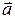 = (2, -3, 5)
= (2, -3, 5)
· параллельно прямой 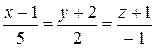
· параллельно оси Ox
· и M1 (3, -1, 0)
Матрицы и определители
Определители и их свойства
n элементов, пронумерованных при помощи n первых натуральных чисел, можно упорядочить различными способами. Всякое расположение чисел 1, 2, 3, … , n в некотором определенном порядке называется перестановкой из n элементов. Число различных перестановок из n элементов равно n! = 1 · 2 · 3 · … · n. Если в некоторой перестановке поменять местами какие-либо два элемента (не обязательно стоящие рядом), а все остальные элементы оставить на месте, то получим новую перестановку − транспозицию.
Будем считать расположение элементов в перестановке в возрастающем порядке нормальным. Назовем инверсией (нарушением, беспорядком) в некоторой перестановке тот факт, когда два ее элемента следуют не в том порядке, в котором они стоят в основной (нормальной) перестановке.
Пример:
5 3 1 2 6 4 − подсчитаем число инверсий в заданной перестановке:
2 + 2 + 1 + 2 + 0 + 0 = 7 инверсий
Назовем перестановку четной, если они содержит четное число инверсий, и нечетной, если они содержит нечетное число инверсий.
Можно доказать, что:
1. Всякая транспозиция меняет четность перестановки на противоположную
2. От данной перестановки можно перейти к любой другой с помощью ряда последовательных транспозиций
3. Число всех четных перестановок их n элементов равно числу всех нечетных перестановок их этих же элементов.
Пусть n2 элементов aij расположены в виде квадратной таблицы, состоящей из n строк и j столбцов.
i = 1, 2, 3, … , n − строки
j = 1, 2, 3, … , n − столбцы
а11 а12 а13 … а1n
а21 а22 а23 … а2n
а31 а32 а33 … а3n
……………………
а n1 а n2 а n3 … а n n
Определителем n-го порядка из n2 элементов называется алгебраическая сумма n! элементов, которые представляют собой всевозможные произведения n элементов, взятые по одному и только по одному в каждой строке и в каждом столбце, причем знак члена равен (-1)t, где t − число инверсий в перестановке вторых индексов элементов членов, когда эти элементы расположены в порядке возрастания первых индексов. Следовательно, член определителя имеет знак «+» при четном t и «-» при нечетном t.
а ij − элемент определителя, стоящий в i-ой строке и в j-ом столбце.
Сокращенно определитель может обозначаться:
D = | aij |

 где i = 1, n ; j = 1, n
где i = 1, n ; j = 1, n
Иначе определитель называют детерминантом.
det A – определитель А.
По определению Δ = ∑(-1)t aα1 aα2 aα3 … aαn
Чтобы определить знак каждого члена определителя располагают элементы данного члена так, чтобы первые индексы шли в натуральном порядке. Затем подсчитывают число инверсий перестановки вторых индексов. Если вторые индексы образуют четную перестановку, то перед членом ставят «+», иначе – «–».
Таким образом, определитель n-го порядка содержит n2 элементов, n! членов, каждый из которых состоит из n множителей.
При n = 1 определитель равен элементу. С ростом порядка определителя число членов растет очень быстро. Определители выше третьего порядка вычисляют с помощью свойств определителя.
Минором некоторого элемента определителя называется определитель порядка на один меньше, получаемый из данного путем вычеркивания строки и столбца, на пересечении которых расположен этот элемент.
Для aij (элемент в i-ой строке и j-ом столбце) Мij – его минор.
Алгебраическое дополнение любого элемента равно минору этого элемента, взятого со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число – нечетное.
Aij – алгебраическое дополнение элемента aij
Aij = (-1)i + j ∙ М ij
Дата: 2019-02-25, просмотров: 341.