Лекции по математике
Раздел 3
Линейная алгебра с элементами аналитической геометрии
Тема 7 Векторная алгебра
7.1 n -мерные векторы и операции над ними. n -мерное векторное пространство.
R1 (a1) R2 (a1; a2) R3 (a1; a2; a3)
В геометрии, механике, физике, экономике часто приходится изучать такие объекты, для задания которых недостаточно трех действительных чисел.
Упорядоченную систему из n - чисел, т. е. конечную последовательность чисел, взятых в определенном порядке, в том в каком они написаны, называем n -мерным вектором.
ai i = 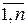 (i = 1, 2, 3, … , n), где n – размерность вектора.
(i = 1, 2, 3, … , n), где n – размерность вектора.
 a = (a1, a2, … , an)
a = (a1, a2, … , an)
 b = (b1, b2, … , bn)
b = (b1, b2, … , bn)
или A, B, C, … , Z.
Векторами могут быть различные объекты физической или математической природы. Важна не природа, а операции, которые можно производить над вектором и свойства, неменяющиеся независимо от геометрического смысла рассматриваемого вектора.
A = (a1, a2, … , an)
B = (b1, b2, … , bn)
Они будут считаться равными, если A = B < = > ai = bi,  i =
i = 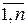
Введем операции сложения и умножения n-мерного вектора на число:
Суммой двух n-мерных векторов называется вектор, компоненты которого сложены, т. е. сумма компонентов слагаемого. A + B = (a1 + b1, … , an + bn).
Можно складывать вектора одной и той же размерности. Сложение векторов подчиняется коммутативному и ассоциативному законам сложения.
A - B = (ai - b1 ,…, an - bn)
A - A = 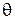 – нулевой вектор.
– нулевой вектор.
Произведением вектора a на α (действительное число) называется вектор, компоненты которого равны произведению на число α соответствующих компонент вектора A.
A ∙ α = α ∙ A = (αa1, αa2, …, αan). Умножение вектора на число подчиняется дистрибутивным и коммуникативному законам.
Свойства:
1. α1 ∙ (α2 ∙ A) = α1 ∙ α2 ∙ A
2. α ∙ (A - B) = α ∙ A - α ∙ B
A ∙ (α1 - α2) = α1 ∙ A - α2 ∙ A
3. 1 ∙ A = A
- 1 ∙ A = -A – противоположенный вектор
4. α ∙ 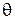 =
= 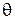 – нулевой вектор
– нулевой вектор
5. α ∙ A = 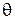 ∙ A – не нулевой вектор и α = 0
∙ A – не нулевой вектор и α = 0
Скалярное произведение A и B – выражение вида:
A ∙ B = a1 ∙ b1 + a2 ∙ b 2 + … + a n ∙ b n
A ∙ B – обозначение скалярного произведения.
Свойства скалярного произведения:
1. A ∙ A ≥ 0, так как A ∙ A = a12 + a22 + … + an2
A ∙ A = 0 < = > A = 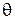
2. A ∙ B = B ∙ A
3. (A + B) ∙ C = A ∙ C + A ∙ B
4. α ∙ (A ∙ B) = (α ∙ A) ∙ B = A ∙ (α ∙ B), α – действительное число
A ∙ A = A2 - скалярный квадрат;
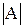 =
= 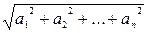 =
= 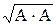 – длина n-мерного вектора;
– длина n-мерного вектора;
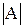 2 = A2 - квадрат длины a равен скалярному квадрату.
2 = A2 - квадрат длины a равен скалярному квадрату.
· Если скалярное произведение равно 0, то вектора называются ортогональными;
· Совокупность векторов называется ортогональной, если вектора этой совокупности попарно параллельны;
· Совокупность векторов называется ортонормированной, если вектора этой совокупности попарно ортогональны и их длины равны 1.
· Если a и b – n -мерные, то их длины связаны со скалярным произведением соотношениями.
1) 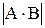 =
= 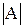 ∙
∙ 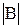 - неравенство Коши – Буняковского;
- неравенство Коши – Буняковского;
2)  ≤
≤ 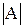 +
+ 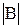 - неравенство треугольника.
- неравенство треугольника.
Углом  (0 ≤
(0 ≤  <
< 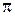 ) между ненулевыми n -мерными векторами A и B называется угол, косинус которого равен
) между ненулевыми n -мерными векторами A и B называется угол, косинус которого равен  = cos
= cos 
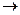 A ∙ B =
A ∙ B = 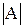 ∙
∙ 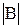 ∙ cos
∙ cos 
n -мерным пространством называется совокупность n -мерных векторов, для которых введены понятия сложения и умножения векторов на число.
Линейное пространство называется евклидовым, если в нем определено скалярное произведение, удовлетворяющее вышеуказанным свойствам.
Пусть задана совокупность вектора в Rn пространстве и известны действительные числа, тогда вектор вида A1 ∙ α1 + A2 ∙ α2 + … + An ∙ αn называется линейной комбинацией вектора.
Замечание. Совокупность векторов (система) отличается от множества векторов тем, что в системе все вектора пронумерованы, а во множестве нет и среди них нет совпадающих.
Матрицы и определители
Определители и их свойства
n элементов, пронумерованных при помощи n первых натуральных чисел, можно упорядочить различными способами. Всякое расположение чисел 1, 2, 3, … , n в некотором определенном порядке называется перестановкой из n элементов. Число различных перестановок из n элементов равно n! = 1 · 2 · 3 · … · n. Если в некоторой перестановке поменять местами какие-либо два элемента (не обязательно стоящие рядом), а все остальные элементы оставить на месте, то получим новую перестановку − транспозицию.
Будем считать расположение элементов в перестановке в возрастающем порядке нормальным. Назовем инверсией (нарушением, беспорядком) в некоторой перестановке тот факт, когда два ее элемента следуют не в том порядке, в котором они стоят в основной (нормальной) перестановке.
Пример:
5 3 1 2 6 4 − подсчитаем число инверсий в заданной перестановке:
2 + 2 + 1 + 2 + 0 + 0 = 7 инверсий
Назовем перестановку четной, если они содержит четное число инверсий, и нечетной, если они содержит нечетное число инверсий.
Можно доказать, что:
1. Всякая транспозиция меняет четность перестановки на противоположную
2. От данной перестановки можно перейти к любой другой с помощью ряда последовательных транспозиций
3. Число всех четных перестановок их n элементов равно числу всех нечетных перестановок их этих же элементов.
Пусть n2 элементов aij расположены в виде квадратной таблицы, состоящей из n строк и j столбцов.
i = 1, 2, 3, … , n − строки
j = 1, 2, 3, … , n − столбцы
а11 а12 а13 … а1n
а21 а22 а23 … а2n
а31 а32 а33 … а3n
……………………
а n1 а n2 а n3 … а n n
Определителем n-го порядка из n2 элементов называется алгебраическая сумма n! элементов, которые представляют собой всевозможные произведения n элементов, взятые по одному и только по одному в каждой строке и в каждом столбце, причем знак члена равен (-1)t, где t − число инверсий в перестановке вторых индексов элементов членов, когда эти элементы расположены в порядке возрастания первых индексов. Следовательно, член определителя имеет знак «+» при четном t и «-» при нечетном t.
а ij − элемент определителя, стоящий в i-ой строке и в j-ом столбце.
Сокращенно определитель может обозначаться:
D = | aij |

 где i = 1, n ; j = 1, n
где i = 1, n ; j = 1, n
Иначе определитель называют детерминантом.
det A – определитель А.
По определению Δ = ∑(-1)t aα1 aα2 aα3 … aαn
Чтобы определить знак каждого члена определителя располагают элементы данного члена так, чтобы первые индексы шли в натуральном порядке. Затем подсчитывают число инверсий перестановки вторых индексов. Если вторые индексы образуют четную перестановку, то перед членом ставят «+», иначе – «–».
Таким образом, определитель n-го порядка содержит n2 элементов, n! членов, каждый из которых состоит из n множителей.
При n = 1 определитель равен элементу. С ростом порядка определителя число членов растет очень быстро. Определители выше третьего порядка вычисляют с помощью свойств определителя.
Минором некоторого элемента определителя называется определитель порядка на один меньше, получаемый из данного путем вычеркивания строки и столбца, на пересечении которых расположен этот элемент.
Для aij (элемент в i-ой строке и j-ом столбце) Мij – его минор.
Алгебраическое дополнение любого элемента равно минору этого элемента, взятого со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число – нечетное.
Aij – алгебраическое дополнение элемента aij
Aij = (-1)i + j ∙ М ij
Виды матриц. Ранг матрицы
Любая таблица, состоящая из чисел, записанных в определенном порядке, содержащая m строк и n столбцов, называется матрицей размерности m×n; число aij – элемент матрицы.
Способы задания матриц:
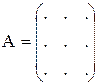
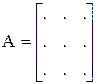
А1×n – матрица-строка
А1×m – матрица-столбец
Матрица, все элементы которой – нули – нулевая матрица.
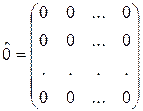
Если m≠n, матрица – прямоугольная;
если m>n, матрица – укороченная;
если m<n, матрица – удлиненная;
если m=n, матрица – квадратная.
|A| – определитель матрицы.
Размерность квадратной матрицы называется ее порядком.
Если определитель квадратной матрицы ≠ 0, то такая матрица – невырожденная (неособенная);
Если определитель квадратной матрицы = 0, то такая матрица – вырожденная (особенная).
Квадратная матрица вида
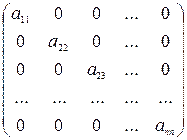
где а11, а22, … , а nn – элементы , распределенные по главной диагонали, называется диагональной матрицей.
Диагональная матрица, все элементы которой по главной диагонали равны 1, называется единичной матрицей (En).
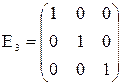
Любое число можно считать матрицей первого порядка.
Если у матрицы переставить местами столбцы со строками, то такая операция называется транспонированием матрицы.
Ат – транспонированная матрица.
|А| = |Ат| (если А – квадратная)
(Ат)т = А
Квадратная матрица называется симметрической, если А = Ат , т.е. aij = aji для любых i и j.
Элементы симметрической матрицы, расположенные симметрично относительно главной диагонали, равны.
Квадратная матрица называется ортогональной, если ее столбцы образуют ортонормированную систему векторов.

 Рассмотрим матрицу А = (aij), i = 1, m ; j = 1, n .
Рассмотрим матрицу А = (aij), i = 1, m ; j = 1, n .
Из этой матрицы можно образовать квадратные матрицы. Определители таких матриц называют минорами данной матрицы. Порядок этих миноров не превышает min(m , n).
Пример:
Для матрицы А5×4 наибольший порядок минора ≤ 4.
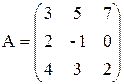 – квадратная матрица 3 порядка:
– квадратная матрица 3 порядка:
9 миноров 1 порядка;
9 миноров 2 порядка;
1 минор 3 порядка;
Рангом матрицы называется максимальный порядок миноров матрицы, отличных от нуля.
Если ранг матрицы r(A) = r, то по крайней мере один из миноров этой матрицы порядка r отличен от нуля, и все миноры более высоки порядков (если они существуют) равны 0.
Ранг матрицы можно вычислить следующими методами:
1) Метод окаймляющих миноров
2) Метод, основанный на элементарных преобразованиях матрицы
Рассмотрим первый метод.








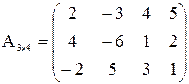

r(A) может принимать значения 1, 2, 3.
Выбираем минор первого порядка:
М1 = -3
Составляем М2, окаймляющий М1 ≠ 0
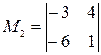 = 21 ≠ 0
= 21 ≠ 0
=> r(A) = 2 или 3.
Составляем М3, окаймляющий М2 ≠ 0
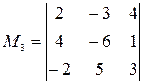 ≠ 0
≠ 0
=> r(A) = 3
Базисным минором матрицы называется минор, не равный нулю, порядок которого равен рангу данной матрицы.
Действий с матрицами
1) Сумма матриц
Складывать можно только матрицы с одинаковым числом строк и столбцов. Суммой матриц А = (aij) и В = (bij) называется новая матрица С = (с ij), элементы которой равны суммам соответствующих элементов матриц А и В.
с ij = aij + bij
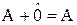
Операции сложения матриц обладают свойствами коммутативности, ассоциативности и дистрибутивности.
2) Умножение матрицы на число
Произведением матрицы А = (aij) на число k называется новая матрица, элементы которой равны произведениям соответствующих элементов матрицы А на число k.
А ∙ k = (k ∙ aij)
k 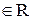
А ∙ k = k ∙ А
3) Умножение матриц
Произведение матрицы А на матрицу В определено только в том случае, когда число столбцов матрицы А равно числу строк матрицы В.
В результате умножения получаем матрицу, у которой столько же строк, сколько у первой матрицы и столько же столбцов, сколько у второй.
А ∙ В ≠ В ∙ А
Am × n ∙ Bn × k = Cm × k
Если произведение матриц возможно, то матрицы А и В называют сцепленными.
Чтобы получить элементы новой матрицы, надо составить сумму произведений элементов какой-либо строки матрицы А на соответствующие элементы какого-либо столбца матрицы В.
с ij = ai 1 ∙ b 1 j + ai 2 ∙ b 2 j + … + ain ∙ bnj
Если А ∙ В = В ∙ А, то матрицы А и В называются перестановочными.
Обратная матрица
Обратная матрица может существовать только для квадратных матриц. Не каждая квадратная матрица имеет обратную матрицу. Если квадратная матрица – не вырожденная, она всегда имеет обратную матрицу, и при том единственную.
Если квадратная матрица вырожденная, то для такой матрицы не существует обратной.
Если существует квадратная матрица В, такая, что А ∙ В = В ∙ А = Е – единичная матрица того же порядка, что и квадратные матрицы А и В, то будем говорить, что матрица А обратима, и матрицу В будем называть обратной для матрицы А.
В = А-1
Справедливы следующие утверждения:
1) Каждая невырожденная матрица обратима;
2) Матрица обратима тогда и только тогда, когда она невырожденная;
3) Обратимая матрица А имеет только одну обратную матрицу.
Нахождение обратной матрицы можно выполнять 2 методами:
1) Метод присоединенной матрицы;
2) Метод, основанный на элементарных преобразованиях матриц.
Рассмотрим первый метод.
Обратную матрицу можно найти по формуле:
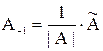
где 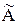 – присоединенная матрица
– присоединенная матрица
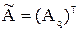
где 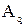 – матрица, элементами которой являются алгебраические дополнения элементов определителя исходной квадратной матрицы.
– матрица, элементами которой являются алгебраические дополнения элементов определителя исходной квадратной матрицы.
Пример:
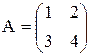
Найти А-1
|A| = 4 ∙ 6 = -2 ≠ 0
А11 = М11 = 4;
А12 = -М12 = -3;
А21 = -М21 = -2;
А22 = М22 = 1.
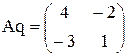
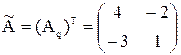

9.5 Элементарные преобразования матриц
Элементарные преобразования матрицы приводят к матрице, эквивалентной исходной.
А ~ В – эквивалентные матрицы.
Эквивалентные матрицы имеют одинаковые ранги.
К элементарным преобразованиям относят:
1) Перестановка местами любых двух столбцов (строк);
2) Умножение каждого элемента произвольного столбца (строки) на число k ≠ 0;
3) Вычеркивание столбца (строки) из нулей;
4) Прибавление к элементам произвольного столбца (строки) соответствующих элементов любого другого столбца (строки), умноженных на произвольное число, отличное от нуля.
5) Транспонирование матрицы
С помощью элементарных преобразований можно находить обратную матрицу:
 1) Приписать справа к матрице А единичную матрицу того же порядка, что и А (А Е);
1) Приписать справа к матрице А единичную матрицу того же порядка, что и А (А Е);

 2) Элементарными преобразованиями строк составленной матрицы за конечное число шагов привести матрицу вида (А Е) к матрице вида (Е В);
2) Элементарными преобразованиями строк составленной матрицы за конечное число шагов привести матрицу вида (А Е) к матрице вида (Е В);
3) Получившаяся в правой половине матрица В и будет обратной матрице А,
В = А-1;
4) Проверка: А ∙ А-1 = Е, либо А-1 ∙ А =Е.
Обратную матрицу можно находить и следующим образом:


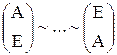
При этом работают со столбцами.
Элементарные преобразования матриц можно применять к нахождению ранга матрицы т.к. если А ~ В, то r(А) = r(В).
Матрица размера m×n вида
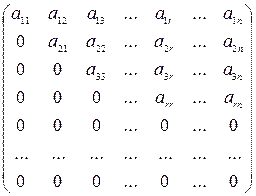
называется трапецеидальной.
а11, а22, а33, … , а rr ≠ 0 (отдельные могут равняться 0).
Каждую матрицу с помощью элементарных преобразований можно превратить в трапецеидальную. Ранг трапецеидальной матрицы равен числу ненулевых строк.
Т.к. элементарные преобразования матрицы не меняют ее ранга, то для отыскания ранга любой матрицы нужно:
1) Преобразовать данную матрицу в трапецеидальную;
2) Подсчитать число ненулевых строк
3) Ранг трапецеидальной матрицы будет равен рангу данной матрицы.
Основные понятия
Рассмотрим систему m линейных уравнений с n неизвестными:
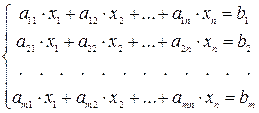 (1)
(1)
xj – неизвестное системы;
aij – коэффициент при неизвестном;
 j = 1, n ;
j = 1, n ;
 i = 1, n ;
i = 1, n ;
bi – свободный член;
 i = 1, m .
i = 1, m .
Рассмотрим различные формы записи системы (1):
а) Краткая запись
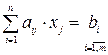 (1`)
(1`)
б) Матричная форма записи
Составим матрицу из коэффициентов при неизвестных:
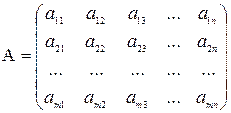
– основная матрица системы (1).
Составим матрицу-столбец неизвестных системы
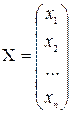
и матрицу-столбец свободных членов

Тогда матричная форма записи системы (1) имеет вид:
А ∙ Х = В
в) Векторная форма записи (1``)
Рассмотрим следующие векторы-столбцы системы (1) вида:
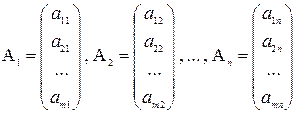
Х = (x 1 , x 2 , x 3 , … , xn) – n переменных.
Составим линейную комбинацию векторов условий вида:
А1 ∙ х1 + А2 ∙ х2 + … + Аn ∙ х n
где х1, х2, … , х n коэффициенты системы (1).
Линейная комбинация векторов – новый вектор, т.е. система (1) в векторной форме имеет вид:
А1 ∙ х1 + А2 ∙ х2 + … + Аn ∙ х n (1```)
Решить систему линейных уравнений значит найти ее решения, или убедиться, что их нет.
Решением системы линейных уравнений (СЛУ) называется такой вектор
 (α1; α2; … ; αn), координаты которого обращают в тождество каждое уравнение системы, если в каждое уравнение системы подставить вместо Х1 – α1, Х2 – α2, … , Хn – αn.
(α1; α2; … ; αn), координаты которого обращают в тождество каждое уравнение системы, если в каждое уравнение системы подставить вместо Х1 – α1, Х2 – α2, … , Хn – αn.
Система уравнений называется совместной, если существует хотя бы одно решение (одно или ∞).
СЛУ называется несовместной, если она не имеет ни одного решения.
Совокупная система уравнений может иметь одно решение ( совместная и определенная) или бесконечное множество решений (совместная и неопределенная). Случай, когда решений конечное множество невозможен.
Две системы называются равносильными, если они имеют одни и те же решения.
Методы решения СЛУ
10.2.1 Решение системы с помощью обратной матрицы
Этот метод может быть применен для решения систем когда m = n. В этом случае основная матрица системы А – квадратичная порядка n.
Если при этом определитель |А| ≠ 0, т.е. квадратная матрица А – невырожденная, то она имеет единственную обратную матрицу.
Рассмотрим систему вида (1), записанную в матричной форме:
А ∙ Х = В
А-1 ∙ А ∙ Х = А-1 ∙ В
Е ∙ Х = А-1 ∙ В
Х = А-1 ∙ В
Х = (α1; α2; … ; αn) – вектора решения
х1 = α1
х1 = α1
. . . . . .
х n = αn
10.2.2 Решение систем линейных уравнений с помощью определителей.
Применяется при условии m = n.
Составим определитель из коэффициентов при неизвестных системы линейных уравнений, у которой n уравнений и n неизвестных. Такой определитель называют основным определителем системы.
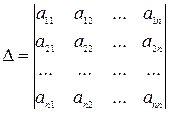
Составим вспомогательные определители для данной системы следующим образом:
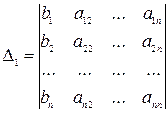
Δ – определитель, который получается из основного определителя заменой его первого столбца столбцом свободных членов системы.
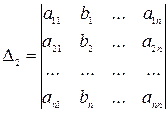
. . . . . . . . . . . . . . . . . . .
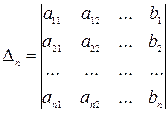
Неизвестные данной системы можно найти по формуле Крамера:
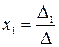 ;
; 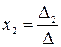 ; … ;
; … ; 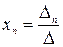 .
.
1) Если основной определитель системы отличен от нуля, то такая система уравнений имеет единственное решение – она совместна и определенна, и это решения находят по формуле Крамера;
2) Если основной определитель системы равен нулю, то система уравнений может быть совместной неопределенной (∞ решений) или несовместной (не имеет решений):
а) Если основной определитель системы равен нулю и все вспомогательные определители равны нулю, то система уравнений имеет ∞ решений;
б) Если основной определитель системы равен нулю и хотя бы один из вспомогательных определителей не равен нулю, то система – несовместна.
Рассмотрим случай 2 а, т.е. Δ = 0; Δ1, Δ2, … , Δn = 0.
Тогда исключают одно из уравнений данной системы (оно является следствием других уравнений системы). Затем выделяют основные переменные (базисные) и свободные переменные, которые могут принимать любые значения из множества действительных чисел.
Если какие-то векторы полученной системы будут линейно независимыми, значит они образуют базис, а следовательно переменные при этих векторах также будут базисными.
Набор переменных, входящих в базис, может быть разным, а количество базисных переменных в каждом наборе – одно и то же.
Иначе за базисные переменные можно принять такие переменные, при которых определитель, составленный из коэффициентов при данных переменных, отличен от нуля.
После того, как выбраны базисные переменные, их выражают в рассматриваемой системе через свободные переменные. Полученная при этом СЛУ и будет являться общим решением исходной системы.
Если свободным переменным придавать любые значения из множества действительных чисел, то будем получать частные решения исходной системы в виде векторов, и таких векторов будет бесконечное множество.
Базисным решением исходной таблицы будет являться вектор, у которого все свободные переменные равны нулю, а базисные переменные равны свободным членам системы общего решения.
Базисное решение называется допустимым, если все координаты вектора базисного решения не отрицательны.
10.2.3 Решение СЛУ методом последовательного исключения переменных.
Этот метод основан на применении элементарных преобразований над системой уравнений, которые преобразуют данную систему уравнений в эквивалентную ей.
Различают два метода исключения переменных: метод Гаусса и метод Жордана – Гаусса (метод полного исключения переменных). Это универсальные методы решения систем линейных уравнений, т.к. их можно применять для решения систем в случае когда m = n и m ≠ n.
Рассмотрим метод Жордана – Гаусса.
Этот метод состоит из нескольких шагов (итераций), которые позволяют за конечное число операций сделать вывод о существовании решения данной системы или о том, что решений нет.
На каждом шаге исключается одна из переменных, которая называется ведущей. Ведущая переменная остается в одном из уравнений, которое также называется ведущим (ключевым). Из оставшихся уравнений ведущая переменная исключается с помощью элементарных преобразований.
Процесс исключения переменных производится с помощью таблиц Гаусса. Таблицей Гаусса обычно называют расширенную матрицу данной системы вида:


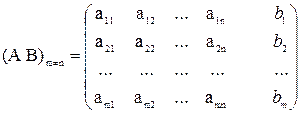
На основании элементарных преобразований над строками расширенной матрицы системы m линейных уравнений с n неизвестными, сформируем правила исключения переменных:
1) Выбираем ведущий элемент, ведущую строку, ведущий столбец.
Каждый элемент ведущей строки делим на ведущий элемент, и результат записываем в такую же по номеру строку новой (эквивалентной) матрицы;
2) Ведущий столбец в эквивалентной матрице превращается в единичный вектор;
3) Если в ведущей строке есть нули, то соответствующие столбцы переписываются без изменения;
4) Если в ведущем столбце есть нули, то соответствующие строки переписываются без изменения;
5) все остальные элементы эквивалентной матрицы находятся по правилу прямоугольника:

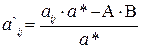
где aij – элемент первой таблицы;
a ` ij – новый элемент эквивалентной таблицы;
a * – ведущий элемент расширенной матрицы;
A – элемент расширенной матрицы, стоящий в ведущей строке;
B – элемент расширенной матрицы, стоящий в ведущем столбце.
6) Все предыдущие пункты повторяются шаг за шагом, пока:
а) либо основная матрица системы будет состоять из единичных векторов (СЛУ имеет единственное решение, она совместна и определенна);
б) либо на некотором шаге преобразованной матрицы в одной из строк все элементы превратятся в нули, и при этом не встретится строка вида:
 (0 0 0 … 0 b), b ≠ 0, (*)
(0 0 0 … 0 b), b ≠ 0, (*)
то строку из нулей вычеркивают, и система будет иметь бесконечное множество решений (она будет совместна и неопределенна).
В этом случае выделяют базисные и свободные переменные. Базисные переменные выражают через свободные, получают общее решение исходной системы, из которого можно получить бесконечное множество частных решений.
Это такие решения, когда все свободные переменные равны нулю, а базисные переменные принимают значения любых действительных чисел.
Если компоненты вектора базисного решения не отрицательны, то это базисное решение будет допустимым базисным решением (опорным решением данной системы).
в) либо на некотором шаге получим строку вида (*), тогда решение системы заканчивается, говорят, что система не совместна, не имеет решений.
Пример:
Решить СЛУ:
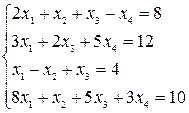
Применим метод Жордана – Гаусса.
Составим расширенную матрицу системы:





0 = -22 – неверно, следовательно система не совместна, не имеет решений.
Система линейных неравенств
12.1 Понятие системы линейных неравенств. Выпуклые множества.
Крайние точки.
Неравенство называется линейным, если содержит переменные только в первой степени, причем отсутствуют и произведения переменных.
Множеством решений неравенства с n неизвестными является одно из двух полупространств, разделенных гиперплоскостью, уравнение которой:
а1х1 + а2х2 + … + а n х n = а
Пусть дано неравенство с двумя переменными:
а1х1 + а2х2 ≤ (≥) а; а1, а2 ≠ 0 (*)
Геометрическим решением такого неравенства будет одна из полуплоскостей, на которые прямая вида а1х1 + а2х2 = 0 разделяет плоскость ХОУ в R2.
Если неравенство нестрогое, то точки, лежащие на данной прямой, удовлетворяют неравенству (*). Точки плоскости, лежащие выше (ниже) этой прямой, могут удовлетворять данному неравенству (*). Для этого следует выбрать любую точку плоскости, не лежащую на этой прямой, и подставить координаты этой точки в неравенство (*).
Если неравенство получается верным, то решением такого неравенства будет та часть плоскости, из которой выбиралась точка.
Обычно в качестве контрольной точки удобно брать начало координат, если прямая не проходит через эту точку.
Множества, элементами которых являются точки, называются точечными. Точечные множества бывают выпуклые и невыпуклые. Если существует хотя бы одна пара точек множества, таких, что отрезок, соединяющий эти точки, не принадлежит целиком этому множеству, то оно называется невыпуклым.
Множество точек называется выпуклым, если вместе с его любыми двумя точками ему принадлежит и весь отрезок, соединяющий эти точки.
Выпуклые множества обладают важными свойствами, которые используются при геометрической интерпретации решений системы линейных неравенств с двумя переменными.
Пересечение двух выпуклых множеств является также выпуклым множеством.
Частными случаями точечных множеств на плоскости служат выпуклые многоугольники. Выпуклым многоугольником называется выпуклая фигура, ограниченная несколькими отрезками, называемыми сторонами многоугольника. Точки, в которых сходятся концы двух соседних сторон, называются крайними (угловыми) точками (вершинами) многоугольника.
Когда вся фигура лежит по одну сторону от прямой, и прямая имеет с фигурой одну общую точку или отрезок, то такая прямая называется опорой прямой.
Каждая сторона выпуклого многоугольника является опорной прямой.
В пространстве R3 понятие выпуклый многогранник – тело, образованное пересечением плоскостей, грани которого – выпуклые многоугольники.
Вершины этого многогранника – крайние (угловые) точки.
Примерами выпуклых многогранников служат шар, параллелепипед, призма и др.
Основные понятия теории вероятностей
ТВ – раздел математики, в котором изучаются случайные явления (события) с устойчивой частостью и выявляются закономерности при массовом их повторении.
В экономике и других областях человеческой деятельности часто приходится иметь дело с событиями, которые невозможно точно предсказать. Так, объем продаж товара зависит от спроса, который может существенно меняться, и от ряда других факторов, учесть которые практически невозможно. При организации производства и осуществлении продаж приходится прогнозировать исход деятельности либо на основе собственного или чужого опыта, либо на основе интуиции, которая в значительной степени тоже опирается на опытные данные.
Чтобы каким-то образом оценить событие, надо учесть или организовать условия, в которых оно происходит или может происходить. Выполнение определенных условий или действий с элементами случайностей для выявления рассматриваемого события носит название опыта (испытания), эксперимента (один или несколько опытов).
Исход – это возможный результат эксперимента.
Событие – это один или несколько исходов эксперимента.
Событие А, В, С называется случайным, если в результате опыта оно может произойти или не произойти.
Событие А, В, С называется достоверным, если оно обязательно появляется в результате опыта.
Событие А, В, С называется невозможным, если оно не появляется в результате опыта.
Например: выпадение снега 30 ноября – случайное событие; ежедневный восход Солнца – достоверное событие; выпадение снега на экваторе – невозможное событие.
Во многих задачах рассматривается схема равновозможных событий.
Например: при бросании игральной кости имеется одна и та же возможность появления цифры от 1 до 6. каждый из равновозможных результатов опытов называется элементарным исходом (простым событием).
Элементарный исход может быть рассмотрен либо как самостоятельное событие, либо как составляющая более сложного события.
Элементарные исходы опыта обозначаются: ω1, ω2,…, ωn.
Множество элементов (может быть конечным или бесконечным):
Ω = {ω1, ω2, … , ωn}.
Можно выделить из этого множества подмножество, которое обладает заданными свойствами и определяет новое событие.
Например: на множестве элементарных исходов при бросании игральной кости можно выделить подмножество таких исходов, которые соответствуют четному числу очков или нечетному числу очков. Множество элементарных исходов:
Ω={ω1, ω2, ω3, ω4, ω5, ω6}, А  .
.
А наступит тогда, когда А={ω2, ω4, ω6};
В наступит тогда, когда В={ω1,ω3,ω5,};
С наступит тогда, когда очки кратны трем С={ω3, ω6}.
Исход называется благоприятствующим, если его появление влечет за собой наступление этого события.
Классификация случайных событий:
Случайные события – это подмножество множества элементарного исхода.
Совокупность всех наблюдаемых событий составляет поле событий опыта.
Событие А произошло, если результатом опыта явился элементарный исход, ω 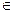 А.
А.
Событие, совпадающее с пустым множеством, называется невозможным.
Событие, совпадающее со всем множеством Ω, называется достоверным.
Два события А и В называются совместными, если в данном опыте они могут появиться одновременно, т.е. возможно их совместное осуществление. Иначе говоря, А и В называются совместными, если соответствующие множества А и В имеют общие элементы. Это определение можно распространить на любое конечное число событий.
Два события А и В называются несовместными, если в результате опыта невозможно их совместное осуществление. Их множества не имеют общих элементов. 
Например: у студента 2 лотерейных билета; введем следующие события: А – выигрыш по одному билету, В – выигрыш по второму билету, А и В – совместные.
Например: производится проверка одного изделия на стандартность; А – изделие стандартно, В – изделие нестандартно, А и В – несовместные.
Несколько событий А1, А2, … , Аn называются попарно совместными, если любые два из них не могут появиться одновременно в данном опыте.
Несколько событий В1, В2, … , Вn образуют полную группу событий в данном опыте, если хотя бы одно из них обязательно произойдет.
Например: попадание и промах при выстреле в мишень; появление одного, двух, трех, четырех, пяти, шести очков при одном подбрасывании игральной кости.
Существуют группы событий, которые обладают тремя свойствами:
1. Образуют полную группу;
2. Несовместные попарно;
3. Равновозможные.
Если события А и Ā образуют полную группу несовместных событий, то они называются противоположными.
Событие называется сложным, если его можно представить в виде комбинации некоторых элементарных событий.
Существует 2 основных вида таких комбинаций:
1. Сумма событий;
2. Произведение событий.
Алгебра событий
Случайные события отождествляются с множеством, поэтому над событиями можно совершать все операции, выполняемые над множествами.
1. А 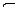 В – событие А влечет за собой событие В, т.е. В происходит всякий раз, как происходит А.
В – событие А влечет за собой событие В, т.е. В происходит всякий раз, как происходит А.
2. А = В – событие А тождественно событию В 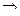 А
А  В и В
В и В  А.
А.
3. А + В – сумма событий, т.е. новое событие, состоящее в появлении хотя бы одного из них (или А, или В, или А и В).
А + В ~ А  В = В
В = В  А
А
А1 + А2 + … + Аn =  Аn.
Аn.
4. А ∙ В – произведение событий – новое событие, состоящее в совместном появлении событий и А, и В.
А ∙ В ~ А  В= В
В= В  А
А
Если А и В несовместны, то произведение этих событий равно пустому множеству.
5. А - В – разность событий – новое событие, состоящее в том, что А происходит, а В не происходит.
6. Ā = Ω - А – новое событие, состоящее в том, что А не происходит. 
А + Ā = Ω – достоверное событие, совпадающее со всем пространством элемен-тарных событий.
Эти операции могут быть представлены в виде диаграмм Вьенна:

13.3 Вероятность события
К основным понятиям ТВ относят вероятность события. Это понятие вводится для количественного описания степени объективной возможности наступления того или иного события в данном опыте.
Вероятность случайного события А рассматривают как функцию случайного события: Р(А) – вероятность события А.
Во многих учебниках по ТВ рассматривается аксиоматическое построение ТВ.
Вероятность события А рассматривается как числовая функция, определенная на некотором классе подмножеств множества Ω, который называется полем событий S, и удовлетворяющая трем аксиомам вероятностей:
1. 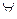 А
А 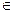 S, Р(А) ≥ 0
S, Р(А) ≥ 0
2. Р(Ω) = 1
3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий:

 Р(А
Р(А  В) = Р(А) + Р(В), А
В) = Р(А) + Р(В), А 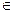 S, В
S, В 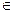 S, А
S, А  В=
В=
Рассмотрим статистическое, классическое, геометрическое определения вероятности случайного события:
1. Статистическое определение вероятности.
Это определение основано на свойстве устойчивости частот.
Пусть производится опыт неоднократно. В результате повторений может появиться некоторое событие А, а может и не появиться. Пусть N – число опытов, которое производится, NA – число опытов, в которых наступило событие А. относительной частотой появления события А в данных опытах называется отношение NA к N:
r(A)= 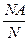 .
.
Вероятностью события А называется число, относительно которого стабилизируется (устанавливается) r(A) при условии, что N  , т.е. при достаточно большом числе опытов, которые производятся в одинаковых условиях:
, т.е. при достаточно большом числе опытов, которые производятся в одинаковых условиях:
Р(А)= 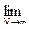 r(A)=
r(A)= 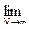
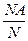 .
.
2. Классическое определение вероятности.
Пусть события А1, А2,…, Аn образуют полную группу равновозможных и попарно несовместных событий. В этом случае говорят, что имеется схема случаев. Вероятностью события А называется отношение числа m исходов, благоприятствующих данному событию, к общему числу n всех возможных исходов опыта, образующих полную группу равновозможных попарно несовместных событий:
Р(А)= 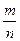 .
.
3. Геометрическая вероятность.
Классическое определение нельзя применять к опыту с бесконечным числом равновозможных исходов. Для описания такой ситуации применимо понятие геометрической вероятности.
Пусть пространством элементарных событий служит множество точек некоторой области Ω, имеющей различную меру (в пространстве R1: мера – длина; в R2: мера – площадь; в R3: мера – объем). Тогда:
Р(А)= 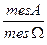 , где
, где
mes А – мера множества А; mes Ω – мера множества Ω, А 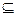 Ω.
Ω.
Элементы комбинаторики
Для решения многих задач, связанных с классическим определением вероятности, потребуется развить технику подсчета всевозможных комбинаций предметов, которая называется комбинаторикой.
Основным средством подсчета является теорема о комбинациях (принцип умножения): имеется конечное множество k групп предметов произвольной природы.
Первая группа содержит n1 предметов: 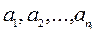 ; вторая группа содержит n2 предметов:
; вторая группа содержит n2 предметов: 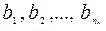 ; …; k-ая группа содержит nk предметов:
; …; k-ая группа содержит nk предметов: 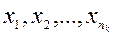 .
.
Можно образовать ровно 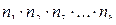 комбинаций этих предметов, содержащих по одному предмету из каждой группы.
комбинаций этих предметов, содержащих по одному предмету из каждой группы.
Выборкой объема К из совокупности n предметов называется любая последовательность предметов из этой совокупности длины К.
Выбранные предметы можно расположить в порядке их появления в последовательности, тогда выборка называется упорядоченной.
Если же условиться не различать выборки, отличающиеся только порядком предметов, то говорим о неупорядоченной выборке.
Предметы в выборке могут повторяться, тогда она называется выборкой с возвращениями. Если повторение запретить, получим выборку без возвращения.
Например: выборка трех призеров из 8 команд – упорядоченная, без возвращений; выбор трехзначного телефонного номера – упорядоченная с возвращением; выборка трех делегатов на научную конференцию – неупорядоченная, без возвращений.
Поскольку при подсчете комбинаций природа предметов не играет роли, то предметы будем считать занумерованными шарами, а выборку – процедурой извлечения этих шаров из урны. Разным схемам извлечения шаров из урны соответствуют выборки с различными свойствами.
Размещением из n предметов по К называется упорядоченная выборка К предметов из n возможных без возвращений.
Число размещений из n предметов по К обозначается 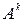 ; n>k.
; n>k.
Схема извлечения шаров.
Имеется урна с n шарами и пустой ящик с К ячейками. Вынимаем из урны шар и кладем его в первую ячейку, затем снова вынимаем шар и кладем его во вторую ячейку, и так далее до заполнения всех К ячеек.
Число размещений из n предметов по К задается равенством:
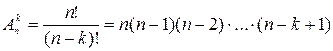 .
.
Действительно, первый шар можно вынуть n способами, второй – (n-1) способами, и т.д., k-ый по счету шар можно вынуть (n-k+1) способами.
По теореме о комбинациях число способов вынуть К шаров равно произведению этих чисел, т.е. справедлива формула 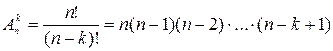 .
.
Перестановкой из n предметов называется размещение из n предметов по n.
Число перестановок n предметов обозначаются через Рn.
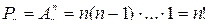
переставить n предметов – значит упорядочить их по-другому, но всякий способ упорядочения можно смоделировать так: поместить все предметы в урну и доставать по одному, укладывая по порядку в ячейки.
Сочетанием изn предметов по К называется неупорядоченная выборка К предметов из n возможных без возвращения.
Число сочетаний из n предметов по К обозначается  .
.
Схема извлечения шаров.
Имеется урна с шарами и пустой мешок. Вынимаем из урны шар и бросаем в мешок, затем снова вынимаем шар и бросаем в мешок, и так далее, пока в мешке не наберется К шаров.
Число сочетаний изn предметов по К задается равенством:
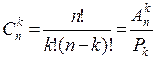 .
.
Действительно, размещение 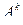 можно получить следующим образом: составить всевозможные сочетания
можно получить следующим образом: составить всевозможные сочетания 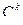 и в каждом из сочетаний произвести всевозможные перестановки, т.е.
и в каждом из сочетаний произвести всевозможные перестановки, т.е. 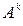 =
= 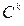 ∙Рk.
∙Рk.
Свойства сочетаний:

размещение с повторениями из n предметов по К называется упорядоченная выборка К предметов из n возможных с возвращениями.
Число размещений с повторениями из n предметов по К обозначаются 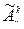 .
.
Схема извлечения шаров.
Имеется урна с n шарами и табличка с К клетками.
Вынимаем из урны шар и записываем его номер в первую клетку, а шар возвращаем обратно в урну.
Повторяем процедуру до заполнения таблички.
Число размещений с повторениями из n предметов по К задается равенством:
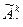 =nk.
=nk.
Первый шар можно выбрать n способами, второй – тоже (т.к. первый возвращается в урну) и т.д.
По теореме о комбинациях получаем формулу:
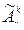 =n ∙ n ∙ n ∙…∙ n=nk.
=n ∙ n ∙ n ∙…∙ n=nk.
Сочетанием из n предметов по К с повторениями называется неупорядоченная выборка из n предметов по К с возвращениями.
Схема извлечения шаров.
Из урны с n пронумерованными шарами вынимаем шар, записываем его номер на бумагу, бумагу кладем в шапку, а шар обратно в урну. Операцию повторяем К раз.
Обозначение: 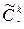 .
.
Можно доказать, что 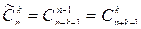 .
.
Сведем полученные результаты в таблицу:
| Выборки | Упорядоченные | Неупорядоченные |
| Без возвращения | 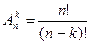
| 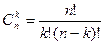
|
| С возвращением | 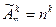
| 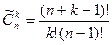
|
При решении задач на подсчет числа выборок нужно ставить два вопроса:
1. Возможны ли повторения выбираемых предметов?
2. Важен ли порядок предметов?
В зависимости от ответов пользуемся соответствующей графой таблицы.
Пример. Студент на экзамене отвечает на 3 из 50 вопросов программы. Он подготовил 40 вопросов. Какова вероятность того, что среди случайным образом выбранных вопросов ему известен хотя бы один? Не менее двух?
Решение:
Припишем каждому вопросу номер от 1 до 50 так, что вопросы, известные студенту, получили бы номера от 1 до 40. результат однократного выбора трех вопросов будем отмечать тройкой номеров {ω1, ω2, ω3}. Пространство элементарных исходов состоит из всех таких троек, причем все тройки таковы, что порядок номеров в тройке несущественен и все цифры в тройке различны. Пусть Ак – случайное событие, состоящее в том, что среди тройки вопросов, доставшихся студенту, ему известно ровно k вопросов. Это случайное событие состоит из тех троек {ω1, ω2, ω3}, в которых ровно k номеров удовлетворяют соотношению 1≤ω≤40, k=0, 1, 2, 3.
Исходя из того, что вопросы выбираются случайным образом, полагаем, что все тройки равновероятны, и приписываем каждому элементарному исходу одну и ту же вероятность:
Р({ω1, ω2, ω3})= 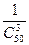
Случайное событие А0 – среди тройки вопросов, доставшихся студенту, ему ни один вопрос не известен – содержит m= 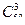 элементарных исходов.
элементарных исходов.
Применяя классическое определение вероятности 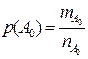 , получаем:
, получаем:
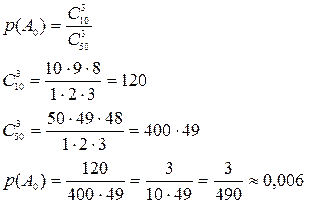
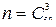 - число всех возможных и равновозможных элементарных исходов испытания.
- число всех возможных и равновозможных элементарных исходов испытания.
Событие А – студент знает хотя бы один вопрос (А≥1) является противоположным событию А0, то для вероятности р(А≥1) получаем:
 .
.
Заметим, что студент, не выучивший 20% вопросов курса (10 из 50 вопросов), почти наверняка – в 99 случаях их 100 – ответит, по крайней мере, на один из предложенных ему вопросов.
Это, правда, еще не является гарантией успешной сдачи экзамена, но…
Найдем вероятность того, что среди случайным образом выбранных вопросов ему известны не менее двух. Событие А≥2 – студент знает не менее двух вопросов из трех. Как и выше, легко находим, что количество элементарных исходов, образующих это событие, задается числом:
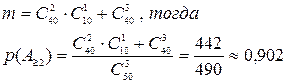
То есть почти в 9 случаях из 10 студентов, не знающих 20% курса, ответит не менее, чем на два вопроса из трех. Это уже гарантия успешной сдачи.
Замечание. Для этой же задачи можно построить другое вероятностное пространство.
Естественно считать, что вопросы выбираются по порядку. Будем считать элементарным исходом эксперимента упорядоченную тройку номеров вопросов (ω1, ω2, ω3). Поскольку все номера различны, то количество элементарных исходов (принцип умножения) равно 50 ∙ 49 ∙ 48. подсчитаем количество элементарных исходов, образующих событие А0. это событие образовано только теми тройками, номера вопросов в которых заключены от 41 до 50. их количество в соответствии с принципом умножения равно 10 ∙ 9 ∙ 8. Тогда:
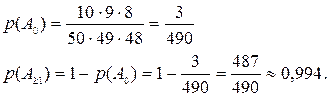
Основные теоремы ТВ
13.4.1 Условная вероятность
Понятие «вероятность» было введено как числовая функция, определенная на поле событий и удовлетворяющая трем основным аксиомам (аксиоматическое построение ТВ). Такая вероятность называется безусловной, она не зависит от дополнительных условий, кроме тех, которыми характеризуется эксперимент. Если же вероятность зависит от каких-либо дополнительных условий, то в этом случае вводится понятие условной вероятности.
Например: студент выучил из 30 билетов 16, из которых 4 четных, 12 нечетных. К моменту прихода студента на экзамен осталось 14 билетов, все они нечетные. Какова вероятность того, что студент получит выученный билет? Если бы не было дополнительного условия (осталось 14 билетов), то вероятность события А (получение выученного билета) по классическому определению была бы следующей:
Р(А) = 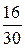
Если учесть дополнительное условие, то вероятность будет следующей:
Р(А) = 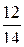
Вероятность события А, найденная в предположении, что событие В уже наступило, называется условной вероятностью события А относительно события В: Р( 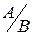 ), РВ(А) и Р(
), РВ(А) и Р(  ),
), 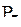 (А).
(А).
Два события называются независимыми, если появление каждого из них не зависит от появления или не появления другого.
Р(А)= Р( 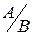 )=Р(
)=Р( 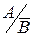 )
)
Р(В)= Р( 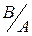 )=Р(
)=Р( 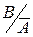 ).
).
Если эти равенства не выполняются, то события называются зависимыми (если вероятность каждого из них меняется, когда становится известно, что другое событие имело место).
Несколько событий называются попарно независимыми, если каждые два их них независимы.
События называются независимыми в совокупности, если вероятность каждого из них не меняется при наступлении других событий, одного или нескольких.
Теорема 1: (о сумме вероятностей попарно несовместных событий):
Если события А1, А2, … , Аn попарно несовместны, то вероятность суммы этих событий равна сумме вероятностей каждого из них:
Р (А1 + А2 + … + Аn) = Р(А1) + Р(А2) + … + Р(Аn)
Р( 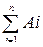 )=
)=  Р(Ai).
Р(Ai).
Теорема 2
Сумма вероятностей противоположных событий равна единице:
Р(А)+ Р(Ā)=1
Р(А)=1- Р(Ā).
Теорема 3
Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий:
Р(А ∙ В)=Р(А) ∙ Р(В).
Следствие
Вероятность совместного наступления нескольких событий, независимых в совокупности, равна произведению их вероятностей:
Р (А1 ∙ А2 ∙ … ∙ Аn)= Р(А1) ∙ Р(А2) ∙ … ∙ Р(Аn).
Теорема 4 (для зависимых событий)
Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(А ∙ В)= Р(А) ∙ Р( 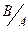 )=Р(В) ∙ Р(
)=Р(В) ∙ Р( 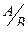 ).
).
Следствие
Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных.
При этом вероятности каждого последующего события вычисляются в предположении, что предыдущие события уже наступили:
Р (А1 ∙ А2 ∙ …Аn-1 ∙ Аn) = 
Теорема 5 (о сумме совместных событий)
Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного наступления:
Р(А+В)=Р(А)+Р(В)-Р(А ∙ В).
Теорема 6
Вероятность появления хотя бы одного из событий А1, А2, … , Аn, независимых в совокупности, вычисляется по формуле:
Р (А1 + А2 + … + Аn) = 1 - Р(Ā1 ∙ Ā2 ∙ … ∙ Ān) = 1 - Р(Ā1) ∙ Р(Ā2) ∙ … ∙ Р(Ān),
где А = А1 + А2 + … + Аn и Ā = Ā1 ∙ Ā2 ∙ … ∙ Ān – противоположные события.
Если вероятности событий Р(Āi)=р все одинаковы для любых i, тогда вероятности Р(Аi)=q 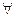 i. Тогда: Р(А1 + А2 + … + Аn) = 1- qn, q = 1- р.
i. Тогда: Р(А1 + А2 + … + Аn) = 1- qn, q = 1- р.
13.4.2 Формула полной вероятности. Формулы Байеса.
Рассмотрим совокупность событий, попарно несовместных и образующих полную группу событий.

 В1, В2,…, Вn, т.е. Bi
В1, В2,…, Вn, т.е. Bi  Bj =
Bj =
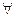 i
i 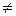 j, В1 + В2 + … + Вn =
j, В1 + В2 + … + Вn = 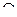
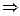 Р(В1)+Р(В2) + … + Р(Вn) = 1.
Р(В1)+Р(В2) + … + Р(Вn) = 1.
Пусть некоторое событие А может наступить лишь при условии появления одного из событий В1, В2,…, Вn. Причем заранее не известно, с каким именно, поэтому совокупность событий В1, В2,…, Вn, попарно несовместных и образующих полную группу событий, называется совместными гипотезами (событие А может наступить только в комбинации с какой-либо из гипотез).
Тогда: А = А ∙ В1 + А ∙ В2 + … + А ∙ Вn , А ∙ Вi, i = 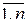 – попарно несовместны. Cобытия А и В1, А и В2,…, А и Вn – зависимые. Необходимо найти Р(А).
– попарно несовместны. Cобытия А и В1, А и В2,…, А и Вn – зависимые. Необходимо найти Р(А).
Р(А) = Р(А ∙ В1 + А ∙ В2 + … + А ∙ Вn) = Р(А ∙ В1) + … +Р(А ∙ Вn) = Р(В1) ∙ Р( 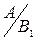 ) + … + Р(Вn) ∙ Р(
) + … + Р(Вn) ∙ Р(  ) – формула полной вероятности.
) – формула полной вероятности.
Р(А)=  – логический перебор всех возможных вариантов наступления события А.
– логический перебор всех возможных вариантов наступления события А.
Пусть при выше перечисленных условиях опыт уже произошел, в результате которого уже появилось событие А. Тогда выясняют, как изменились вероятности гипотез после опыта. При тех же самых условиях, что и при выводе формулы полной вероятности, если в условии задачи отмечается факт наступления события А в данном опыте, тогда ставится вопрос: какова условная вероятность каждой из гипотез после того, как событие А уже произошло. Т.е. необходимо переоценить вероятность гипотез после опыта, т.е. Р( 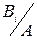 ). Ответ на поставленный вопрос дают формулы Байеса:
). Ответ на поставленный вопрос дают формулы Байеса:
Р( 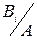 ) =
) = 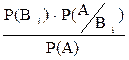 , где
, где
i= 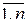 я
я
Р(А) – полная вероятность.
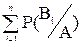 = 1.
= 1.
Закон больших чисел
Под законом больших чисел (ЗБЧ) понимают ряд теорем, описывающих закономерности поведения усредненных результатов большого числа n повторных испытаний, если результат каждого отдельного испытания есть случайное событие или СВ.
Смысл ЗБЧ состоит в том, что при большом числе повторных испытаний их усредненный результат практически перестает быть случайным и может быть предсказан с высокой достоверностью, т.е. с вероятностью, близкой к единице.
ЗБЧ описывается рядом теорем, при доказательстве которых используется неравенство Чебышева. Теоремы:
- теорема Чебышева
- теорема Бернулли
- теорема Ляпунова (центральная предельная теорема ТВ).
Неравенство Чебышева
Вероятность того, что отклонение СВ от ее М(Х) превзойдет по абсолютной величине положительное число ε, не больше дроби, числитель которой есть Д(Х), а знаменатель есть ε2.
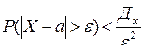 .
.
Если рассматривать противоположное событие для 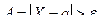 , т.е.
, т.е.
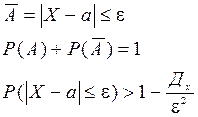
Теорема Чебышева
Пусть имеется конечная последовательность Х1, Х2,…, Хn независимых СВ с одним и тем же М(Х): М(Х1) = М(Х2) = … = М(Хn) = а. И дисперсиями, ограниченными одной и той же постоянной С: Д(Х1)  С, Д(Х2)
С, Д(Х2)  С, …, Д(Хn)
С, …, Д(Хn)  С. Тогда, каково бы ни было данное положительное число ε, вероятность события стремится к единице при n→∞.
С. Тогда, каково бы ни было данное положительное число ε, вероятность события стремится к единице при n→∞.
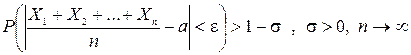 .
.
Число СВ достаточно велико. Теорема Чебышева показывает, что при достаточно большом числе измерений некоторой СВ средне арифметическое значение этих измерений приближается к М(Х).
Теорема Бернулли
Если вероятность наступления события А в каждом из n независимых испытаний постоянна, а число испытаний достаточно велико, то вероятность того, что частость события А будет как угодно мало отличаться от его вероятности сколь угодно близка к единице.
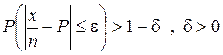 .
.
Ценность этой теоремы заключается в том, что если вероятность события А в отдельном испытании не известна, то ее можно с достаточной для практических целей точностью и надежностью принять равной относительной частоте r(A) появления этого события в длинной серии таких испытаний.
Р(А) ≈ r(A), n → ∞.
Теорема Ляпунова
Если СВ представляет собой сумму очень большого числа взаимно независимых СВ, влияние каждой из которых на всю сумму ничтожно мало, то СВ имеет распределение, близкое к нормальному.
Эта теорема имеет огромное значение для практики. Согласно ей можем ожидать, что изменчивость таких показателей, как рост и обхват груди человека, определение возраста и пола, вес отдельного яблока или булки хлеба, величина ошибки измерения некоторого физического показателя и т.д. должны хорошо описываться законом нормального распределения, что и наблюдается на практике.
Системы случайных величин
При исследовании случайных явлений часто приходится рассматривать одновременно несколько СВ. Их совокупность можно представить как многомерную СВ.
Двумерная СВ – СВ (X, Y), каждое возможное появление которой представляет собой пару чисел (x; y) случайных величин X и Y, рассматриваемые совместно.
СВ, рассматриваемые совместно, образуют систему двух СВ.
| Y | X | |||
| x1 | x2 | … | xn | |
| y1 | P(x1,y1) | P(x2,y1) | … | P(xn,y1) |
| … | … | … | … | … |
| ym | P(x1,ym) | P(x2,ym) | … | P(xn,ym) |
Двумерная СВ – дискретная.
Каждой паре значений (xi; yj) ставится в соответствие вероятность появления этой пары Р(X = хi, Y = yj).
Общей характеристикой двумерной СВ является функция распределения вероятностей, которая представляет собой вероятность события, что X<x, Y<y.
F(x, y) = P(X < x, Y < y).
Для НСВ функция распределения записывается в виде интеграла:
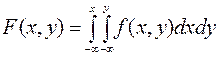 , где f(x, y) – плотность распределения вероятностей двумерной СВ.
, где f(x, y) – плотность распределения вероятностей двумерной СВ.
Вероятность совместного появления ДСВ (двумерной) записывается в виде:
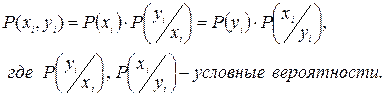
Для НСВ плотность распределения вероятностей записывается в виде:
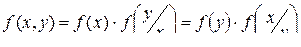 .
.
Лекции по математике
Раздел 3
Линейная алгебра с элементами аналитической геометрии
Тема 7 Векторная алгебра
7.1 n -мерные векторы и операции над ними. n -мерное векторное пространство.
R1 (a1) R2 (a1; a2) R3 (a1; a2; a3)
В геометрии, механике, физике, экономике часто приходится изучать такие объекты, для задания которых недостаточно трех действительных чисел.
Упорядоченную систему из n - чисел, т. е. конечную последовательность чисел, взятых в определенном порядке, в том в каком они написаны, называем n -мерным вектором.
ai i = 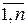 (i = 1, 2, 3, … , n), где n – размерность вектора.
(i = 1, 2, 3, … , n), где n – размерность вектора.
 a = (a1, a2, … , an)
a = (a1, a2, … , an)
 b = (b1, b2, … , bn)
b = (b1, b2, … , bn)
или A, B, C, … , Z.
Векторами могут быть различные объекты физической или математической природы. Важна не природа, а операции, которые можно производить над вектором и свойства, неменяющиеся независимо от геометрического смысла рассматриваемого вектора.
A = (a1, a2, … , an)
B = (b1, b2, … , bn)
Они будут считаться равными, если A = B < = > ai = bi,  i =
i = 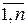
Введем операции сложения и умножения n-мерного вектора на число:
Суммой двух n-мерных векторов называется вектор, компоненты которого сложены, т. е. сумма компонентов слагаемого. A + B = (a1 + b1, … , an + bn).
Можно складывать вектора одной и той же размерности. Сложение векторов подчиняется коммутативному и ассоциативному законам сложения.
A - B = (ai - b1 ,…, an - bn)
A - A = 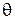 – нулевой вектор.
– нулевой вектор.
Произведением вектора a на α (действительное число) называется вектор, компоненты которого равны произведению на число α соответствующих компонент вектора A.
A ∙ α = α ∙ A = (αa1, αa2, …, αan). Умножение вектора на число подчиняется дистрибутивным и коммуникативному законам.
Свойства:
1. α1 ∙ (α2 ∙ A) = α1 ∙ α2 ∙ A
2. α ∙ (A - B) = α ∙ A - α ∙ B
A ∙ (α1 - α2) = α1 ∙ A - α2 ∙ A
3. 1 ∙ A = A
- 1 ∙ A = -A – противоположенный вектор
4. α ∙ 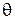 =
= 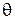 – нулевой вектор
– нулевой вектор
5. α ∙ A = 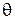 ∙ A – не нулевой вектор и α = 0
∙ A – не нулевой вектор и α = 0
Скалярное произведение A и B – выражение вида:
A ∙ B = a1 ∙ b1 + a2 ∙ b 2 + … + a n ∙ b n
A ∙ B – обозначение скалярного произведения.
Свойства скалярного произведения:
1. A ∙ A ≥ 0, так как A ∙ A = a12 + a22 + … + an2
A ∙ A = 0 < = > A = 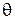
2. A ∙ B = B ∙ A
3. (A + B) ∙ C = A ∙ C + A ∙ B
4. α ∙ (A ∙ B) = (α ∙ A) ∙ B = A ∙ (α ∙ B), α – действительное число
A ∙ A = A2 - скалярный квадрат;
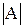 =
= 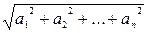 =
= 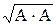 – длина n-мерного вектора;
– длина n-мерного вектора;
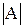 2 = A2 - квадрат длины a равен скалярному квадрату.
2 = A2 - квадрат длины a равен скалярному квадрату.
· Если скалярное произведение равно 0, то вектора называются ортогональными;
· Совокупность векторов называется ортогональной, если вектора этой совокупности попарно параллельны;
· Совокупность векторов называется ортонормированной, если вектора этой совокупности попарно ортогональны и их длины равны 1.
· Если a и b – n -мерные, то их длины связаны со скалярным произведением соотношениями.
1) 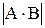 =
= 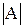 ∙
∙ 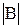 - неравенство Коши – Буняковского;
- неравенство Коши – Буняковского;
2)  ≤
≤ 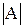 +
+ 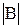 - неравенство треугольника.
- неравенство треугольника.
Углом  (0 ≤
(0 ≤  <
< 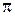 ) между ненулевыми n -мерными векторами A и B называется угол, косинус которого равен
) между ненулевыми n -мерными векторами A и B называется угол, косинус которого равен  = cos
= cos 
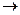 A ∙ B =
A ∙ B = 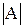 ∙
∙ 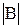 ∙ cos
∙ cos 
n -мерным пространством называется совокупность n -мерных векторов, для которых введены понятия сложения и умножения векторов на число.
Линейное пространство называется евклидовым, если в нем определено скалярное произведение, удовлетворяющее вышеуказанным свойствам.
Пусть задана совокупность вектора в Rn пространстве и известны действительные числа, тогда вектор вида A1 ∙ α1 + A2 ∙ α2 + … + An ∙ αn называется линейной комбинацией вектора.
Замечание. Совокупность векторов (система) отличается от множества векторов тем, что в системе все вектора пронумерованы, а во множестве нет и среди них нет совпадающих.
Дата: 2019-02-25, просмотров: 380.