Случайная величина (СВ) – функция Х=Х(ω), определенная на множестве элементарных событий Ω.
СВ может принять то или иное значение из некоторого числового множества, но не известно какое именно.
СВ обозначаются заглавными латинскими буквами X, Y, Z. Принимаемые ими значения – соответствующими строчными буквами x1, x2,…, xn; y1, y2,…, yn; z1, z2,…, zn.
Если существует конечное или счетное множество значений СВ таких, что Р(Х=хi)=Pi, (i= 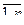 ) и
) и 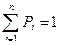 (
( 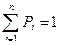 - сходящийся ряд), то СВ Х называется дискретной (ДСВ).
- сходящийся ряд), то СВ Х называется дискретной (ДСВ).
Если значение, которое может принять данная СВ Х в некотором опыте заполняет конечный или бесконечный промежуток (а;b) числовой оси ОХ, то СВ Х называется непрерывной (НСВ).
14.2 Закон распределения ДСВ. Способы его задания. Функция распределения ДСВ.
Поведение ДСВ Х описывается ее законом распределения, который представляет собой функцию Р(Х), определяющую для каждого возможного значения хi ДСВ Х соответствующую вероятность появления этого значения.
Р(хi)= Р(Х=хi)=Pi , i= 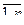 - аналитический способ задания закона распределения ДСВ.
- аналитический способ задания закона распределения ДСВ.
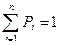 , т.е. в результате испытания ДСВ Х обязательно примет одно из своих допустимых значений.
, т.е. в результате испытания ДСВ Х обязательно примет одно из своих допустимых значений.
Закон распределения ДСВ удобно задавать в виде таблицы, которая называется рядом распределения ДСВ.
| Хi | x1 | x2 | … | xn | … |
| Pi | P1 | P2 | … | Pn | … |
Закон распределения ДСВ может быть задан графически:
|


 |
|
Функция распределения (интегральный закон распределения) СВ Х – функция F(X), выражающая вероятность того, что СВ Х примет значение, меньшее чем х: F(X) =Р(Х < х).
Это понятие существует для ДСВ и НСВ.
Пусть СВ Х – дискретная, заданная рядом распределения вида ( ∙ ).
Х1 < х2 < х3 < …< хn.
Составим функцию распределения и построим ее график.
1. -  < х
< х  х1 ; F(х1) = Р(Х < х1) = 0
х1 ; F(х1) = Р(Х < х1) = 0
2. х1 < х  х2 ; F(х2) = Р(Х < х2) = Р(Х = х1) = P1
х2 ; F(х2) = Р(Х < х2) = Р(Х = х1) = P1
3. х2 < х  х3 ; F(х3) = Р(Х < х3) = Р(Х = х1)+Р(Х = х2) = P1 + P2
х3 ; F(х3) = Р(Х < х3) = Р(Х = х1)+Р(Х = х2) = P1 + P2
………………………………
n. хn < х 
 ; F(
; F( 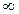 )=Р(Х<
)=Р(Х< 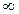 ) = Р(Х = х1) + Р(Х= Х2) +…+ Р(Х= хn) = 1.
) = Р(Х = х1) + Р(Х= Х2) +…+ Р(Х= хn) = 1.

F(X)= 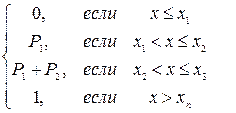
Функция распределения ДСВ постоянна на промежутках 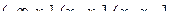 ,
,
i = 1, … , n - 1, в точках х1, х2, х3 и т.д. функция имеет скачки (разрыв I рода), равные вероятности того, что СВ примет соответствующее значение.
Функция распределения полностью характеризует СВ с вероятностной точки зрения – она есть одна из форм закона распределения СВ.
Основные свойства функции распределения:
1. F(X) – неубывающая функция
x2 > х1, то F(х2) ≥ F(х1), F(X) ≥0
2. 0  F(X)
F(X)  1
1
3. Р(а  Х
Х  b) = F(b)-F(а)
b) = F(b)-F(а)
4. F(- 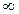 ) = 0
) = 0
F(+ 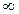 ) = 1
) = 1
F(- 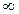 ) =
) = 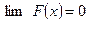
F(+ 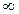 )=
)= 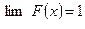
14.3 Непрерывная случайная величина и способы ее задания
Непрерывная случайная величина (НСВ) – СВ, возможные значения которой непрерывно заполняют некоторый промежуток.
Для НСВ функция распределения F(X)=Р(Х<х) будет непрерывной.
Вероятность того, что НСВ Х примет одно определенное значение равна нулю, т.е. Р(Х= хi)=0.
Р(а  Х
Х  b) = F(b) - F(а)
b) = F(b) - F(а)
Рассматривается СНВ Х в интервале (а; b). Пусть а = х1; b = х1 + ∆х, ∆х 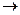 0.
0.
Р(х1  Х
Х  х1 + ∆х) = F(х1 + ∆х) - F(х1)
х1 + ∆х) = F(х1 + ∆х) - F(х1)
Пусть ∆х 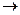 0, т.к. СВ Х – непрерывная, то функция распределения F(X) является непрерывной функцией. Значит, при ∆х
0, т.к. СВ Х – непрерывная, то функция распределения F(X) является непрерывной функцией. Значит, при ∆х  0, ∆F(X) = F(х1 + ∆х) - F(х1)
0, ∆F(X) = F(х1 + ∆х) - F(х1)  0
0 
Р(х1  Х < х1 + ∆х) = F(х1 + ∆х) - F(х1)
Х < х1 + ∆х) = F(х1 + ∆х) - F(х1)  0,
0,
Р(х1  Х<х1 + ∆х) = Р(Х = х1) + Р(а<Х<b) = 0.
Х<х1 + ∆х) = Р(Х = х1) + Р(а<Х<b) = 0.
Нет смысла говорить, что НСВ приняла конкретное значение. Говорят лишь о вероятности того, что НСВ попала на конкретный интервал (даже сколь угодно малый).
Равенство Р(Х = хi) = 0 означает, что при неограниченном повторении испы-тания значение хi СВ будет принимать сколь угодно редко.
Для НСВ справедливо равенство:
Р(а  Х < b) = Р(а < Х
Х < b) = Р(а < Х  b) = Р(а
b) = Р(а  Х
Х  b) = Р(а < Х < b).
b) = Р(а < Х < b).
График функции распределения (интегральной функции) есть непрерывная функция.
Может иметь следующий вид:

Если а 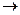 -
- 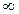 , b
, b 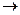
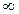 :
:

Задание НСВ при помощи функции распределения не является единственным. НСВ может быть задана с помощью дифференциальной функции распределения вероятностей (плотность распределения вероятности).
Функция f(x), заданная в виде f(x) = F′(X), где F(X) – функция распределения НСВ Х, называется плотностью вероятности НСВ.
Рассмотрим вероятностный смысл функции f(x):
f(x) = F′(X) = 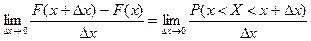 ММсредняя плотность распределения вероятности на промежутке (х; х + ∆х).
ММсредняя плотность распределения вероятности на промежутке (х; х + ∆х).
Тогда предел средней плотности определяет среднюю плотность распределения вероятности в каждой точке х.
График функции f(x) называется кривой Гаусса.
Свойства функции распределения:
1. f(x) ≥ 0
2. 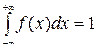
f(x)dx является элементом вероятности.
F(x)dx = dF(x)≈∆F = F(x + ∆х) - F(x) = Р(х1<Х<х1 + ∆х)
3. Если НСВ рассматривается на конечном промежутке (а; b), то
Р (а < Х < b) = 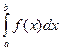 .
.
4. Если f(x) задана, значит СВ Х – непрерывная, тогда:
F(X) = 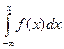 - несобственный интеграл с переменным верхним пределом
- несобственный интеграл с переменным верхним пределом
F(X) = Р(Х<х) = Р( - 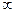 <Х<х) = F(X) - F( -
<Х<х) = F(X) - F( - 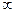 ) =
) = 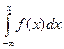 .
.
Дата: 2019-02-25, просмотров: 342.