Совокупность линейных неравенств с общими неизвестными называется системой линейных неравенств.
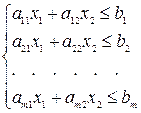
Неравенства могут быть одного смысла (≤ или ≥) или разного.
Множество решений, которое удовлетворяет каждому неравенству системы, называется решением системы неравенств.
Системы неравенств, имеющие хотя бы одно решение, называются совместными.
Если системы неравенств не имеют решений, то они – несовместные.
Если система m неравенств с двумя переменными совместна, то множеством решений такой системы является выпуклый многоугольник или выпуклая многоугольная область (неограниченная).
Множеством решений системы линейных неравенств с двумя переменными может быть:
1) Точка;
2) Пустое множество;
3) Выпуклый многоугольник;
4) Выпуклая неограниченная область.
Пример:
Построить область решений системы линейных неравенств:
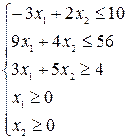
1) 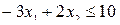
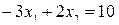 – прямая l1
– прямая l1
x1 = 0; x2 = 5
x2 = 0; x1 = -10/5
О(0;0) ≤ 10 – верно
2) 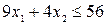
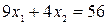 – прямая l2
– прямая l2
x1 = 0; x2 = 6,2
x2 = 0; x1 = 14
О(0;0) ≤ 56 – верно
3) 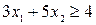
 – прямая l3
– прямая l3
x1 = 0; x2 = 4/3
 x2 = 0; x1 = 0,8
x2 = 0; x1 = 0,8
О(0;0) ≥ 4 – неверно
Точки пересечения:
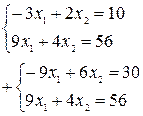
10х2 = 86
х2 = 8,6
-3х1 = 7,2
х1 = 2,4
(2,4; 8,6)
Раздел 4
Теория вероятностей с элементами
математической статистики
Случайные события и их вероятности
Основные понятия теории вероятностей
ТВ – раздел математики, в котором изучаются случайные явления (события) с устойчивой частостью и выявляются закономерности при массовом их повторении.
В экономике и других областях человеческой деятельности часто приходится иметь дело с событиями, которые невозможно точно предсказать. Так, объем продаж товара зависит от спроса, который может существенно меняться, и от ряда других факторов, учесть которые практически невозможно. При организации производства и осуществлении продаж приходится прогнозировать исход деятельности либо на основе собственного или чужого опыта, либо на основе интуиции, которая в значительной степени тоже опирается на опытные данные.
Чтобы каким-то образом оценить событие, надо учесть или организовать условия, в которых оно происходит или может происходить. Выполнение определенных условий или действий с элементами случайностей для выявления рассматриваемого события носит название опыта (испытания), эксперимента (один или несколько опытов).
Исход – это возможный результат эксперимента.
Событие – это один или несколько исходов эксперимента.
Событие А, В, С называется случайным, если в результате опыта оно может произойти или не произойти.
Событие А, В, С называется достоверным, если оно обязательно появляется в результате опыта.
Событие А, В, С называется невозможным, если оно не появляется в результате опыта.
Например: выпадение снега 30 ноября – случайное событие; ежедневный восход Солнца – достоверное событие; выпадение снега на экваторе – невозможное событие.
Во многих задачах рассматривается схема равновозможных событий.
Например: при бросании игральной кости имеется одна и та же возможность появления цифры от 1 до 6. каждый из равновозможных результатов опытов называется элементарным исходом (простым событием).
Элементарный исход может быть рассмотрен либо как самостоятельное событие, либо как составляющая более сложного события.
Элементарные исходы опыта обозначаются: ω1, ω2,…, ωn.
Множество элементов (может быть конечным или бесконечным):
Ω = {ω1, ω2, … , ωn}.
Можно выделить из этого множества подмножество, которое обладает заданными свойствами и определяет новое событие.
Например: на множестве элементарных исходов при бросании игральной кости можно выделить подмножество таких исходов, которые соответствуют четному числу очков или нечетному числу очков. Множество элементарных исходов:
Ω={ω1, ω2, ω3, ω4, ω5, ω6}, А 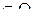 .
.
А наступит тогда, когда А={ω2, ω4, ω6};
В наступит тогда, когда В={ω1,ω3,ω5,};
С наступит тогда, когда очки кратны трем С={ω3, ω6}.
Исход называется благоприятствующим, если его появление влечет за собой наступление этого события.
Классификация случайных событий:
Случайные события – это подмножество множества элементарного исхода.
Совокупность всех наблюдаемых событий составляет поле событий опыта.
Событие А произошло, если результатом опыта явился элементарный исход, ω 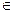 А.
А.
Событие, совпадающее с пустым множеством, называется невозможным.
Событие, совпадающее со всем множеством Ω, называется достоверным.
Два события А и В называются совместными, если в данном опыте они могут появиться одновременно, т.е. возможно их совместное осуществление. Иначе говоря, А и В называются совместными, если соответствующие множества А и В имеют общие элементы. Это определение можно распространить на любое конечное число событий.
Два события А и В называются несовместными, если в результате опыта невозможно их совместное осуществление. Их множества не имеют общих элементов. 
Например: у студента 2 лотерейных билета; введем следующие события: А – выигрыш по одному билету, В – выигрыш по второму билету, А и В – совместные.
Например: производится проверка одного изделия на стандартность; А – изделие стандартно, В – изделие нестандартно, А и В – несовместные.
Несколько событий А1, А2, … , Аn называются попарно совместными, если любые два из них не могут появиться одновременно в данном опыте.
Несколько событий В1, В2, … , Вn образуют полную группу событий в данном опыте, если хотя бы одно из них обязательно произойдет.
Например: попадание и промах при выстреле в мишень; появление одного, двух, трех, четырех, пяти, шести очков при одном подбрасывании игральной кости.
Существуют группы событий, которые обладают тремя свойствами:
1. Образуют полную группу;
2. Несовместные попарно;
3. Равновозможные.
Если события А и Ā образуют полную группу несовместных событий, то они называются противоположными.
Событие называется сложным, если его можно представить в виде комбинации некоторых элементарных событий.
Существует 2 основных вида таких комбинаций:
1. Сумма событий;
2. Произведение событий.
Алгебра событий
Случайные события отождествляются с множеством, поэтому над событиями можно совершать все операции, выполняемые над множествами.
1. А 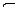 В – событие А влечет за собой событие В, т.е. В происходит всякий раз, как происходит А.
В – событие А влечет за собой событие В, т.е. В происходит всякий раз, как происходит А.
2. А = В – событие А тождественно событию В 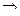 А
А  В и В
В и В  А.
А.
3. А + В – сумма событий, т.е. новое событие, состоящее в появлении хотя бы одного из них (или А, или В, или А и В).
А + В ~ А  В = В
В = В  А
А
А1 + А2 + … + Аn =  Аn.
Аn.
4. А ∙ В – произведение событий – новое событие, состоящее в совместном появлении событий и А, и В.
А ∙ В ~ А  В= В
В= В  А
А
Если А и В несовместны, то произведение этих событий равно пустому множеству.
5. А - В – разность событий – новое событие, состоящее в том, что А происходит, а В не происходит.
6. Ā = Ω - А – новое событие, состоящее в том, что А не происходит. 
А + Ā = Ω – достоверное событие, совпадающее со всем пространством элемен-тарных событий.
Эти операции могут быть представлены в виде диаграмм Вьенна:

13.3 Вероятность события
К основным понятиям ТВ относят вероятность события. Это понятие вводится для количественного описания степени объективной возможности наступления того или иного события в данном опыте.
Вероятность случайного события А рассматривают как функцию случайного события: Р(А) – вероятность события А.
Во многих учебниках по ТВ рассматривается аксиоматическое построение ТВ.
Вероятность события А рассматривается как числовая функция, определенная на некотором классе подмножеств множества Ω, который называется полем событий S, и удовлетворяющая трем аксиомам вероятностей:
1. 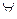 А
А 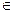 S, Р(А) ≥ 0
S, Р(А) ≥ 0
2. Р(Ω) = 1
3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий:

 Р(А
Р(А  В) = Р(А) + Р(В), А
В) = Р(А) + Р(В), А 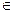 S, В
S, В 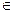 S, А
S, А  В=
В=
Рассмотрим статистическое, классическое, геометрическое определения вероятности случайного события:
1. Статистическое определение вероятности.
Это определение основано на свойстве устойчивости частот.
Пусть производится опыт неоднократно. В результате повторений может появиться некоторое событие А, а может и не появиться. Пусть N – число опытов, которое производится, NA – число опытов, в которых наступило событие А. относительной частотой появления события А в данных опытах называется отношение NA к N:
r(A)= 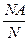 .
.
Вероятностью события А называется число, относительно которого стабилизируется (устанавливается) r(A) при условии, что N  , т.е. при достаточно большом числе опытов, которые производятся в одинаковых условиях:
, т.е. при достаточно большом числе опытов, которые производятся в одинаковых условиях:
Р(А)= 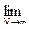 r(A)=
r(A)= 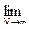
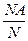 .
.
2. Классическое определение вероятности.
Пусть события А1, А2,…, Аn образуют полную группу равновозможных и попарно несовместных событий. В этом случае говорят, что имеется схема случаев. Вероятностью события А называется отношение числа m исходов, благоприятствующих данному событию, к общему числу n всех возможных исходов опыта, образующих полную группу равновозможных попарно несовместных событий:
Р(А)= 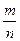 .
.
3. Геометрическая вероятность.
Классическое определение нельзя применять к опыту с бесконечным числом равновозможных исходов. Для описания такой ситуации применимо понятие геометрической вероятности.
Пусть пространством элементарных событий служит множество точек некоторой области Ω, имеющей различную меру (в пространстве R1: мера – длина; в R2: мера – площадь; в R3: мера – объем). Тогда:
Р(А)= 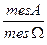 , где
, где
mes А – мера множества А; mes Ω – мера множества Ω, А 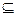 Ω.
Ω.
Элементы комбинаторики
Для решения многих задач, связанных с классическим определением вероятности, потребуется развить технику подсчета всевозможных комбинаций предметов, которая называется комбинаторикой.
Основным средством подсчета является теорема о комбинациях (принцип умножения): имеется конечное множество k групп предметов произвольной природы.
Первая группа содержит n1 предметов: 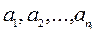 ; вторая группа содержит n2 предметов:
; вторая группа содержит n2 предметов: 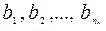 ; …; k-ая группа содержит nk предметов:
; …; k-ая группа содержит nk предметов: 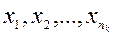 .
.
Можно образовать ровно 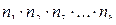 комбинаций этих предметов, содержащих по одному предмету из каждой группы.
комбинаций этих предметов, содержащих по одному предмету из каждой группы.
Выборкой объема К из совокупности n предметов называется любая последовательность предметов из этой совокупности длины К.
Выбранные предметы можно расположить в порядке их появления в последовательности, тогда выборка называется упорядоченной.
Если же условиться не различать выборки, отличающиеся только порядком предметов, то говорим о неупорядоченной выборке.
Предметы в выборке могут повторяться, тогда она называется выборкой с возвращениями. Если повторение запретить, получим выборку без возвращения.
Например: выборка трех призеров из 8 команд – упорядоченная, без возвращений; выбор трехзначного телефонного номера – упорядоченная с возвращением; выборка трех делегатов на научную конференцию – неупорядоченная, без возвращений.
Поскольку при подсчете комбинаций природа предметов не играет роли, то предметы будем считать занумерованными шарами, а выборку – процедурой извлечения этих шаров из урны. Разным схемам извлечения шаров из урны соответствуют выборки с различными свойствами.
Размещением из n предметов по К называется упорядоченная выборка К предметов из n возможных без возвращений.
Число размещений из n предметов по К обозначается 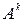 ; n>k.
; n>k.
Схема извлечения шаров.
Имеется урна с n шарами и пустой ящик с К ячейками. Вынимаем из урны шар и кладем его в первую ячейку, затем снова вынимаем шар и кладем его во вторую ячейку, и так далее до заполнения всех К ячеек.
Число размещений из n предметов по К задается равенством:
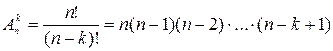 .
.
Действительно, первый шар можно вынуть n способами, второй – (n-1) способами, и т.д., k-ый по счету шар можно вынуть (n-k+1) способами.
По теореме о комбинациях число способов вынуть К шаров равно произведению этих чисел, т.е. справедлива формула 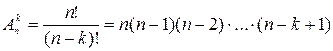 .
.
Перестановкой из n предметов называется размещение из n предметов по n.
Число перестановок n предметов обозначаются через Рn.
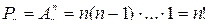
переставить n предметов – значит упорядочить их по-другому, но всякий способ упорядочения можно смоделировать так: поместить все предметы в урну и доставать по одному, укладывая по порядку в ячейки.
Сочетанием изn предметов по К называется неупорядоченная выборка К предметов из n возможных без возвращения.
Число сочетаний из n предметов по К обозначается  .
.
Схема извлечения шаров.
Имеется урна с шарами и пустой мешок. Вынимаем из урны шар и бросаем в мешок, затем снова вынимаем шар и бросаем в мешок, и так далее, пока в мешке не наберется К шаров.
Число сочетаний изn предметов по К задается равенством:
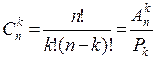 .
.
Действительно, размещение 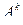 можно получить следующим образом: составить всевозможные сочетания
можно получить следующим образом: составить всевозможные сочетания 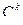 и в каждом из сочетаний произвести всевозможные перестановки, т.е.
и в каждом из сочетаний произвести всевозможные перестановки, т.е. 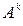 =
= 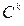 ∙Рk.
∙Рk.
Свойства сочетаний:

размещение с повторениями из n предметов по К называется упорядоченная выборка К предметов из n возможных с возвращениями.
Число размещений с повторениями из n предметов по К обозначаются 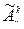 .
.
Схема извлечения шаров.
Имеется урна с n шарами и табличка с К клетками.
Вынимаем из урны шар и записываем его номер в первую клетку, а шар возвращаем обратно в урну.
Повторяем процедуру до заполнения таблички.
Число размещений с повторениями из n предметов по К задается равенством:
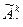 =nk.
=nk.
Первый шар можно выбрать n способами, второй – тоже (т.к. первый возвращается в урну) и т.д.
По теореме о комбинациях получаем формулу:
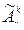 =n ∙ n ∙ n ∙…∙ n=nk.
=n ∙ n ∙ n ∙…∙ n=nk.
Сочетанием из n предметов по К с повторениями называется неупорядоченная выборка из n предметов по К с возвращениями.
Схема извлечения шаров.
Из урны с n пронумерованными шарами вынимаем шар, записываем его номер на бумагу, бумагу кладем в шапку, а шар обратно в урну. Операцию повторяем К раз.
Обозначение: 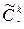 .
.
Можно доказать, что 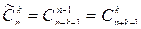 .
.
Сведем полученные результаты в таблицу:
| Выборки | Упорядоченные | Неупорядоченные |
| Без возвращения | 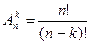
| 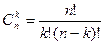
|
| С возвращением | 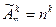
| 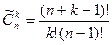
|
При решении задач на подсчет числа выборок нужно ставить два вопроса:
1. Возможны ли повторения выбираемых предметов?
2. Важен ли порядок предметов?
В зависимости от ответов пользуемся соответствующей графой таблицы.
Пример. Студент на экзамене отвечает на 3 из 50 вопросов программы. Он подготовил 40 вопросов. Какова вероятность того, что среди случайным образом выбранных вопросов ему известен хотя бы один? Не менее двух?
Решение:
Припишем каждому вопросу номер от 1 до 50 так, что вопросы, известные студенту, получили бы номера от 1 до 40. результат однократного выбора трех вопросов будем отмечать тройкой номеров {ω1, ω2, ω3}. Пространство элементарных исходов состоит из всех таких троек, причем все тройки таковы, что порядок номеров в тройке несущественен и все цифры в тройке различны. Пусть Ак – случайное событие, состоящее в том, что среди тройки вопросов, доставшихся студенту, ему известно ровно k вопросов. Это случайное событие состоит из тех троек {ω1, ω2, ω3}, в которых ровно k номеров удовлетворяют соотношению 1≤ω≤40, k=0, 1, 2, 3.
Исходя из того, что вопросы выбираются случайным образом, полагаем, что все тройки равновероятны, и приписываем каждому элементарному исходу одну и ту же вероятность:
Р({ω1, ω2, ω3})= 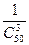
Случайное событие А0 – среди тройки вопросов, доставшихся студенту, ему ни один вопрос не известен – содержит m= 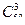 элементарных исходов.
элементарных исходов.
Применяя классическое определение вероятности 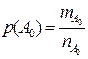 , получаем:
, получаем:
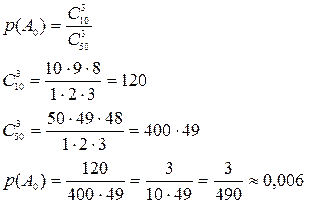
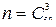 - число всех возможных и равновозможных элементарных исходов испытания.
- число всех возможных и равновозможных элементарных исходов испытания.
Событие А – студент знает хотя бы один вопрос (А≥1) является противоположным событию А0, то для вероятности р(А≥1) получаем:
 .
.
Заметим, что студент, не выучивший 20% вопросов курса (10 из 50 вопросов), почти наверняка – в 99 случаях их 100 – ответит, по крайней мере, на один из предложенных ему вопросов.
Это, правда, еще не является гарантией успешной сдачи экзамена, но…
Найдем вероятность того, что среди случайным образом выбранных вопросов ему известны не менее двух. Событие А≥2 – студент знает не менее двух вопросов из трех. Как и выше, легко находим, что количество элементарных исходов, образующих это событие, задается числом:
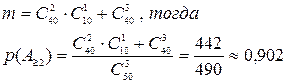
То есть почти в 9 случаях из 10 студентов, не знающих 20% курса, ответит не менее, чем на два вопроса из трех. Это уже гарантия успешной сдачи.
Замечание. Для этой же задачи можно построить другое вероятностное пространство.
Естественно считать, что вопросы выбираются по порядку. Будем считать элементарным исходом эксперимента упорядоченную тройку номеров вопросов (ω1, ω2, ω3). Поскольку все номера различны, то количество элементарных исходов (принцип умножения) равно 50 ∙ 49 ∙ 48. подсчитаем количество элементарных исходов, образующих событие А0. это событие образовано только теми тройками, номера вопросов в которых заключены от 41 до 50. их количество в соответствии с принципом умножения равно 10 ∙ 9 ∙ 8. Тогда:
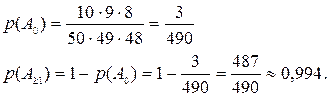
Основные теоремы ТВ
13.4.1 Условная вероятность
Понятие «вероятность» было введено как числовая функция, определенная на поле событий и удовлетворяющая трем основным аксиомам (аксиоматическое построение ТВ). Такая вероятность называется безусловной, она не зависит от дополнительных условий, кроме тех, которыми характеризуется эксперимент. Если же вероятность зависит от каких-либо дополнительных условий, то в этом случае вводится понятие условной вероятности.
Например: студент выучил из 30 билетов 16, из которых 4 четных, 12 нечетных. К моменту прихода студента на экзамен осталось 14 билетов, все они нечетные. Какова вероятность того, что студент получит выученный билет? Если бы не было дополнительного условия (осталось 14 билетов), то вероятность события А (получение выученного билета) по классическому определению была бы следующей:
Р(А) = 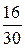
Если учесть дополнительное условие, то вероятность будет следующей:
Р(А) = 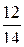
Вероятность события А, найденная в предположении, что событие В уже наступило, называется условной вероятностью события А относительно события В: Р( 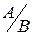 ), РВ(А) и Р(
), РВ(А) и Р(  ),
), 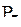 (А).
(А).
Два события называются независимыми, если появление каждого из них не зависит от появления или не появления другого.
Р(А)= Р( 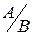 )=Р(
)=Р( 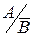 )
)
Р(В)= Р( 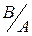 )=Р(
)=Р( 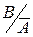 ).
).
Если эти равенства не выполняются, то события называются зависимыми (если вероятность каждого из них меняется, когда становится известно, что другое событие имело место).
Несколько событий называются попарно независимыми, если каждые два их них независимы.
События называются независимыми в совокупности, если вероятность каждого из них не меняется при наступлении других событий, одного или нескольких.
Теорема 1: (о сумме вероятностей попарно несовместных событий):
Если события А1, А2, … , Аn попарно несовместны, то вероятность суммы этих событий равна сумме вероятностей каждого из них:
Р (А1 + А2 + … + Аn) = Р(А1) + Р(А2) + … + Р(Аn)
Р( 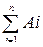 )=
)=  Р(Ai).
Р(Ai).
Теорема 2
Сумма вероятностей противоположных событий равна единице:
Р(А)+ Р(Ā)=1
Р(А)=1- Р(Ā).
Теорема 3
Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий:
Р(А ∙ В)=Р(А) ∙ Р(В).
Следствие
Вероятность совместного наступления нескольких событий, независимых в совокупности, равна произведению их вероятностей:
Р (А1 ∙ А2 ∙ … ∙ Аn)= Р(А1) ∙ Р(А2) ∙ … ∙ Р(Аn).
Теорема 4 (для зависимых событий)
Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(А ∙ В)= Р(А) ∙ Р( 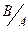 )=Р(В) ∙ Р(
)=Р(В) ∙ Р( 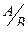 ).
).
Следствие
Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных.
При этом вероятности каждого последующего события вычисляются в предположении, что предыдущие события уже наступили:
Р (А1 ∙ А2 ∙ …Аn-1 ∙ Аn) = 
Теорема 5 (о сумме совместных событий)
Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного наступления:
Р(А+В)=Р(А)+Р(В)-Р(А ∙ В).
Теорема 6
Вероятность появления хотя бы одного из событий А1, А2, … , Аn, независимых в совокупности, вычисляется по формуле:
Р (А1 + А2 + … + Аn) = 1 - Р(Ā1 ∙ Ā2 ∙ … ∙ Ān) = 1 - Р(Ā1) ∙ Р(Ā2) ∙ … ∙ Р(Ān),
где А = А1 + А2 + … + Аn и Ā = Ā1 ∙ Ā2 ∙ … ∙ Ān – противоположные события.
Если вероятности событий Р(Āi)=р все одинаковы для любых i, тогда вероятности Р(Аi)=q 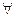 i. Тогда: Р(А1 + А2 + … + Аn) = 1- qn, q = 1- р.
i. Тогда: Р(А1 + А2 + … + Аn) = 1- qn, q = 1- р.
13.4.2 Формула полной вероятности. Формулы Байеса.
Рассмотрим совокупность событий, попарно несовместных и образующих полную группу событий.

 В1, В2,…, Вn, т.е. Bi
В1, В2,…, Вn, т.е. Bi  Bj =
Bj =
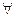 i
i 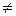 j, В1 + В2 + … + Вn =
j, В1 + В2 + … + Вn = 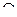
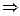 Р(В1)+Р(В2) + … + Р(Вn) = 1.
Р(В1)+Р(В2) + … + Р(Вn) = 1.
Пусть некоторое событие А может наступить лишь при условии появления одного из событий В1, В2,…, Вn. Причем заранее не известно, с каким именно, поэтому совокупность событий В1, В2,…, Вn, попарно несовместных и образующих полную группу событий, называется совместными гипотезами (событие А может наступить только в комбинации с какой-либо из гипотез).
Тогда: А = А ∙ В1 + А ∙ В2 + … + А ∙ Вn , А ∙ Вi, i = 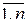 – попарно несовместны. Cобытия А и В1, А и В2,…, А и Вn – зависимые. Необходимо найти Р(А).
– попарно несовместны. Cобытия А и В1, А и В2,…, А и Вn – зависимые. Необходимо найти Р(А).
Р(А) = Р(А ∙ В1 + А ∙ В2 + … + А ∙ Вn) = Р(А ∙ В1) + … +Р(А ∙ Вn) = Р(В1) ∙ Р( 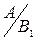 ) + … + Р(Вn) ∙ Р(
) + … + Р(Вn) ∙ Р(  ) – формула полной вероятности.
) – формула полной вероятности.
Р(А)=  – логический перебор всех возможных вариантов наступления события А.
– логический перебор всех возможных вариантов наступления события А.
Пусть при выше перечисленных условиях опыт уже произошел, в результате которого уже появилось событие А. Тогда выясняют, как изменились вероятности гипотез после опыта. При тех же самых условиях, что и при выводе формулы полной вероятности, если в условии задачи отмечается факт наступления события А в данном опыте, тогда ставится вопрос: какова условная вероятность каждой из гипотез после того, как событие А уже произошло. Т.е. необходимо переоценить вероятность гипотез после опыта, т.е. Р( 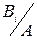 ). Ответ на поставленный вопрос дают формулы Байеса:
). Ответ на поставленный вопрос дают формулы Байеса:
Р( 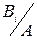 ) =
) = 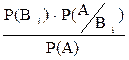 , где
, где
i= 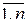 я
я
Р(А) – полная вероятность.
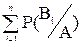 = 1.
= 1.
Дата: 2019-02-25, просмотров: 355.