Рассмотрим методы решения задач, в которых один и тот же опыт повторяется несколько раз. В результате каждого опыта может появиться или не появиться некоторое событие А. причем интересует не результат отдельного опыта, а общее число появления события А в серии испытаний.

Повторные испытания называются независимыми относительно события А, если вероятность появления события А в любом из этих испытаний не зависит от результатов других испытаний.

Например: несколько выстрелов будут независимыми испытаниями, если прицеливание производится перед каждым выстрелом заново. В противном случае выстрелы – зависимые испытания.

Независимые испытания могут производиться в одинаковых или различных условиях.

Пусть вероятность наступления события А в каждом из независимых испытаний одна и та же Р(А) = р, (0 < р < 1). Тогда вероятность не наступления события А = q (она не меняется от испытания к испытанию), (р + q = 1). Такая схема испытаний называется схемой Бернулли.

Если производится n (n < 10) независимых испытаний, в каждом из которых появляется событие А с вероятностью р, то вероятность того, что это событие А появится в этих n испытаниях m раз выражается формулой Бернулли:

Р_m,n = P_n(m) =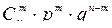

Эту формулу обычно называют биномиальным распределением вероятностей.

Если требуется определить вероятность того, что при n независимых испытаниях событие А появится от m₁ до m₂ раз, то, пользуясь теоремой сложения вероятностей для несовместных событий (попарно), применяют формулу:

.

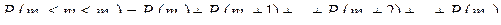К типу задач на биномиальное распределение относятся и задачи на нахождение наивероятнейшего числа появлений события в независимых испытаниях.

Число m₀ называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях m₀ раз (Р_n­(m₀)) не меньше вероятности остальных возможных исходов испытаний.

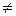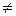Если р 0, р 1, то m₀ можно найти по следующей формуле:

n ∙ р – q 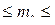n ∙ р + р.

Если:

1. n ∙ р-q – дробное число, то существует только одно m_0;

2. n ∙ р-q – целое, то существует два m₀, которые отличаются друг от друга на единицу;

3. n ∙ р – целое, то m₀₌n ∙ р.

Если число испытаний велико (n>10), вычисления вероятностей по формуле биномиального распределения становится громоздким. В таких случаях используют приближенные методы расчета Р_n­(m), Р_n­(m₁≤m≤m₂). Математически эти формулы выражаются в форме локальной и интегральной теорем Муавра-Лапласа.

Локальная теорема.

Р_n­(m) 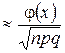 , где

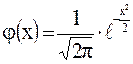 - функция Гаусса

.

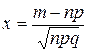Функция Гаусса нормированная, четная ( ).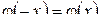

Параметры n, р, q, m имеют тот же смысл, что и в формуле Бернулли.

Интегральная теорема.

Если 0 < p < 1, n > 10

Р_n­(m₁ ≤ m ≤ m₂) 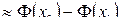, где

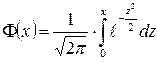 - функция Лапласа.

Φ(-х) = -Φ(х)

 , .

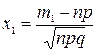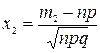Чем больше n, тем точнее формулы локальной и интегральной теорем.

Если число независимых испытаний велико, а вероятность появления события А в каждом испытании очень мала, то используют приближенную формулу Пуассона:

Р_n(m) 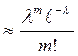 , λ=n ∙ р.

Эта формула применима для редких явлений (событий). Достигаемое приближение при заданном значении n зависит от значения λ. Чем меньше λ, тем лучше приближение.