В теории потребительского потребления и предпочтения существуют два подхода в определении полезности:
- кардионалистская теория, измеряющая полезность в абсолютном выражении (в количестве ютелей);
- ординалистическая (порядковая) теория, построенная на ранжировании потребляемых благ.
Кривая безразличия показывает различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.
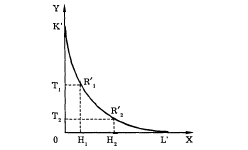
Рис. 4—6. Кривая безразличия
Допустим, что благо X является пепси-колой, а благо Y — гамбургером. Допустим, что потребителю все равно, съесть ли 3 гамбургера, запив их одной бутылкой пепси-колы (точка R’1), или съесть один гамбургер, запив его тремя бутылками пепси-колы (точка R’2) (см. рис. 4—6).
Кривая безразличия представляет все множество комбинаций пепси-колы и гамбургеров, имеющих одинаковую, с точки зрения потребителя, полезность. Чем правее и выше расположена кривая безразличия, тем большее удовлетворение приносят представленные ею комбинации двух благ. Множество кривых безразличия называется картой кривых безразличия (рис. 4—7).
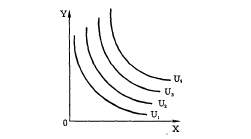
Рис. 4—7. Карта кривых безразличия
Кривые безразличия имеют отрицательный наклон, выпуклы относительно начала координат и никогда не пересекаются друг с другом. Поэтому через любую точку можно провести лишь одну кривую безразличия. Аппарат кривых безразличия имеет важное значение в теории поведения потребителя.
Зона замещения. 3она замещения (субституции) — участок кривой безразличия, в котором возможна эффективная замена одного блага другим.
Рассмотрим кривую безразличия RS (рис. 4—8). Количество блага X, равное 0Т, представляет минимально необходимую величину потребления блага X, от которого потребитель не может отказаться, как бы ни было велико предлагаемое взамен благо Y. Аналогично 0М есть минимально необходимая величина потребления блага Y. Взаимная замена благ X и Y имеет смысл только в пределах отрезка RS. Вне его замена исключается и два блага выступают как независимые друг от друга.
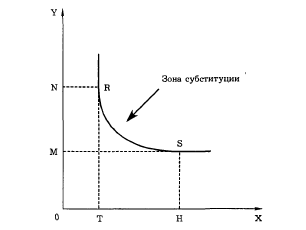
Рис. 4—8. Зона замещения (субституции)
Бюджетное ограничение, линия цен, прямая расходов — все комбинации товаров, которые потребитель имеет возможность купить на располагаемую сумму (бюджет) при данных ценах этих товаров; характеризует совокупность допустимых вариантов выбора набора товаров потребителем при условии полного расходования им имеющегося дохода.
Бюджетные ограничения для двух товаров выражаются формулой:
Px*x + Py*y = I
где Рx — цена товара X;
Py— цена товара Y;
х — количество товара X;
y — количество товара Y;
I — доход потребителя.
Правило долей. Если функция полезности потребителя имеет вид:
TU(x,y) = xayb
а располагаемый доход потребителя:
Px*x + Py*y = I
то определить оптимальный объем потребляемых благ можно по формулам:
x = 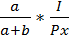 ; у =
; у = 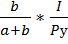
Равновесие потребителя — оптимальное правило покупки набора товаров — точка касания линии бюджетного ограничения с кривой безразличия — оптимальный набор товаров потребителя, находящегося в равновесии.
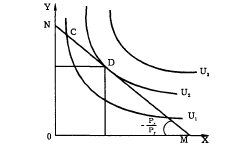
Рис. Равновесие потребителя достигается в точке D.
Пример 1.
Индивидуум имеет доход в размере I = 26 и желает приобрести рациональный набор из двух благ Х и У. Цена Рх =2, цена Ру = 4. Определим равновесие потребителя и величину совокупной полезности TU.
| Q | TUx | TUy |
| 1 | 12 | 20 |
| 2 | 22 | 38 |
| 3 | 30 | 52 |
| 4 | 36 | 60 |
| 5 | 40 | 62 |
Построим дополнительную таблицу.
| Q | TUx | MUx | MUx/Px | Ранг | TUу | MUу | MUу/Pу | Ранг |
| 1 | 12 | 12 | 6 | 1 | 20 | 20 | 5 | 2 |
| 2 | 22 | 10 | 5 | 3 | 38 | 18 | 4,5 | 4 |
| 3 | 30 | 8 | 4 | 5 | 52 | 14 | 3,5 | 6 |
| 4 | 36 | 6 | 3 | 7 | 60 | 8 | 2 | 9 |
| 5 | 40 | 4 | 2 | 9 | 62 | 2 | 0,5 | 10 |
Порядок (ранг) каждой покупки определяем по взвешенной предельной полезности. Первым мы покупаем товар Х, т.е. его взвешенная предельная полезность самая высокая (=6), затем товар У (5) и товар Х (5) и т.д.
А теперь суммируем наши покупки
2+4+2+4+2+4+2+4+2+4 = 30 → бюджета не хватает
Следовательно мы должны убрать самую невыгодную покупку – это будет последний товар У, цена которого равна 4.
Наш бюджет будет полностью израсходован, если мы купим 5 товаров Х и 4 товара У
2*5 + 4*4 = 26
При этом совокупная полезность будет равна
TU = 12+20+10+18+8+14+6+8+4 =100 или TU = 40х + 60у = 100
Пример 2.
Уравнение совокупной полезности TU =12 x 2/3 y 1/3 , доход потребителя I = 54, цена товаров рх =5, ру =3. Определить количество товаров х и у в состоянии равновесия.
Воспользуемся правилом долей для определения оптимального набора товаров Х и У.
x = 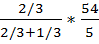 = 7,2 у =
= 7,2 у = 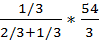 =6
=6
Определим формулу дохода потребителя
5x + 3y = I → 5*7,2 + 3*6 = 54
Глава 5. Теория фирмы
Фирма, как и покупатель, является экономическим агентом. Но если покупатель приобретает товары/услуги для личного или домашнего пользования, то фирма приобретает товары для дальнейшей их переработки, с целью производства товаров и их продажи.
То, что фирма покупает для свой деятельности является факторами производства, и к ним относятся: капитал (основные фонды), человеческие ресурсы, сырье и материалы и пр.
Фирма также как и покупатель, действует на рынке рационально, т.е. она хочет заплатить за факторы производства не больше, чем это необходимо.
Любой фактор производства подчиняется закону убывающей предельной производительности, который гласит, что «с ростом использования какого-либо фактора производства (при неизменности остальных) рано или поздно достигается такая точка, в которой дополнительное его применение нецелесообразно.
Для того чтобы понять этот закон, введем новые понятия.
Совокупный продукт (Q ) - это количество экономического блага, произведенное с использованием некоторого количества переменного фактора.
Совокупная выручка (доход) ( TR ) – объем произведенной продукции в денежном выражении.
TR = P * Q
Средний продукт – это количество экономического блага, приходящегося на единицу переменного фактора (производительность фактора)
AP = 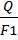
Предельный продукт – это прирост совокупного продукта, полученного в результате приращения предельного фактора (как правило, на единицу)
MP = 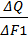
MRP – предельный продукт, выраженный в денежной форме.
MRP = MP *Р
Рассмотрим действие закона убывающей предельной производительности по рис.5-1.
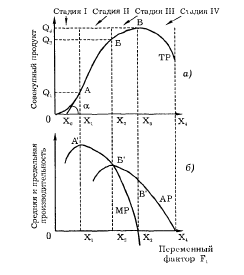
Рис. 5—1. Рост переменного фактора, стадии производства
В точке А. Предельная и средняя производительности растут, причем MP > АР. В т.А предельный продукт достигает своего максимума.
На второй стадии предельный продукт снижается, а средний продукт растет, и в т.Б МР=АР.
На третьей стадии предельный и средний продукт падают, причем предельный продукт падает быстрее. МР ˂ АР. В конце третьей стадии МР=0, а дальше – становится величиной отрицательной. Величина совокупного продукта после т.В начинает сокращаться.
Таким образом, четвертая стадия уже отражает неэффективное производство, когда отдача от переменного фактора носит отрицательный характер.
Поэтому факторы производства используются в производстве только тогда, когда их производительность представляет собой положительную величину.
Спрос на ресурсы является производным от спроса на потребительские блага.
Закон убывающей предельной производительности носит не абсолютный, а относительный характер. Во-первых, он применим лишь на краткосрочном отрезке времени, когда хотя бы один из факторов производства остается неизменным. Во-вторых, технический прогресс постоянно раздвигает его границы.
Правило наименьших издержек
По аналогии с теорией поведения покупателей это правило может быть выражено следующей формулой
 =
=  = … =
= … = 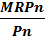
где MRP 1, MRP 2 … MRPn – предельные производительности в денежной форме фактора 1,2 …n
Р1, Р2 … Р n – цены единицы фактора 1,2 …n
Правило наименьших издержек обеспечивает равновесие производителя.
Дата: 2019-02-25, просмотров: 411.