Правило максимизации прибыли является дальнейшим развитием правила минимизации издержек. Оно отражает грамотные пропорции между факторами производства.

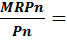                  =  = … =  1  или MPR_i = P_i

Изокванты.Предположим, что в производстве жевательной резинки используются только два ресурса F₁ и F₂, например труд и капитал (рис. 5-4).

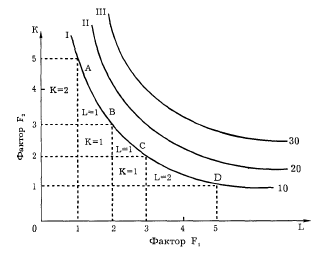
Рис. 5—4. Изокванты

При заданной технологии один и тот же выпуск продукции (10 тыс. жевательных резинок) может быть обеспечен с большим применением капитала (как в точке А) или с большим привлечением труда (как в точке D). Возможны и промежуточные варианты (точки В и С). Если мы соединим все сочетания ресурсов, использование которых обеспечивает одинаковый объем выпуска продукции, то получатся изокванты. Если изокванта является непрерывной линией, то число возможных комбинаций ресурсов будет бесконечным, что обеспечивает чрезвычайную гибкость принимаемых фирмой решений по организации производства продукции.

Изокванта, или кривая постоянного (равного) продукта (iso quant), — кривая, представляющая бесконечное множество комбинаций факторов производства (ресурсов), обеспечивающих одинаковый выпуск продукции. Изокванты для процесса производства означают то же, что и кривые безразличия для процесса потребления. Они обладают аналогичными свойствами: имеют отрицательный наклон, выпуклы относительно начала координат и не пересекаются друг с другом. Изокванта, лежащая выше и правее другой, представляет собой больший объем выпускаемой продукции, например, 20 тыс жевательных резинок, 30 тыс. штук и т.д. Однако, в отличие от кривых безразличия, где суммарное удовлетворение потребителя точно измерить нельзя, изокванты показывают реальные уровни производства: 10 тыс, 20 тыс, 30 тыс и т.д. Совокупность изоквант, каждая из которых показывает максимальный выпуск продукции, достигаемый при использовании определенных сочетаний ресурсов, называется картой изоквант (isoquant map).

Изокоста. Изокоста – это прямая равных издержек.

Если мы возьмем два фактора производства – труд (L) и капитал (К), каждый из которых имеет свою цену, то получим следующий график (рис.5-6)

Изокоста представляет собой график прямой с разными комбинациями использованных ресурсов, сумма которых равна одинаковым затратам на производство.

С = wL + rK  ,

где С – сумма затрат

w – производительность труда одной единицы труда (например, одного рабочего)

L – количество единиц труда (например, количество рабочих)

r – процентная ставка на капитал

К – количество капитала

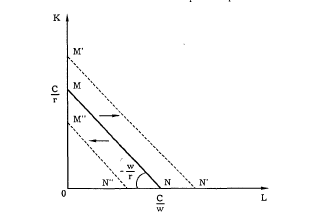
Рис. 5—6. Изокоста

Как видно из графика, в точке М используется только капитал, который можно выразить как М = . В точке N, используется только труд, количество которого равно L = .

Рост бюджета производителя или снижение цен ресурсов сдвигает изокосту вправо, а сокращение бюджета или рост цен — влево (рис. 5—6). Касание изокванты с изокостой определяет положение равновесия производителя, поскольку позволяет достичь максимального объема производства при имеющихся ограниченных средствах, которые можно затратить на покупку ресурсов.

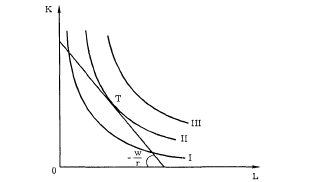
Рис. 5—7. Равновесие производителя

Путь развития и экономия от масштаба. Предположим, что цены ресурсов остаются неизменными, тогда как бюджет производителя постоянно растет. Соединив точки пересечения изоквант с изокостами, мы получим линию 0S — "путь развития" (аналогичную линии уровня жизни в теории поведения потребителя). Эта линия показывает темпы роста соотношения между факторами в процессе расширения производства.

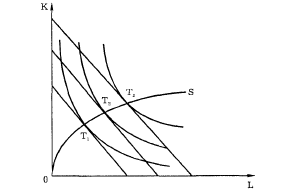
Рис. 5—8. Кривая ''путь развития"

1) Если расстояния между изоквантами уменьшаются, это свидетельствует о том, что существует возрастающая экономия от масштаба, т. е. увеличение выпуска достигается при относительной экономии ресурсов (рис. 5—9).

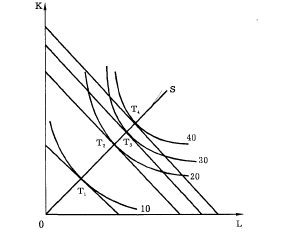
Рис. 5—9. Возрастающая экономия от масштаба

В случае возрастающей экономии от масштаба фирме необходимо наращивать объем производства, так как это приводит к относительной экономии имеющихся ресурсов.

2) Если расстояния между изоквантами увеличиваются, это свидетельствует об убывающей экономии от масштаба (рис. 5—10).

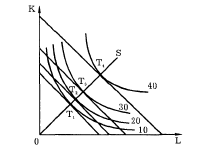
Рис. 5—10. Убывающая экономия от масштаба

Убывающая экономия от масштаба свидетельствует о том, что минимально эффективный размер предприятия уже достигнут и дальнейшее наращивание производства нецелесообразно.

3) В случае, когда увеличение производства требует пропорционального увеличения ресурсов, говорят о постоянной экономии от масштаба (рис. 5—11).

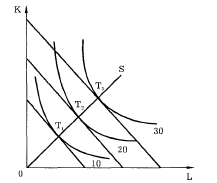
Рис. 5—11. Постоянная экономия от масштаба