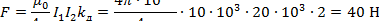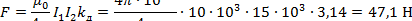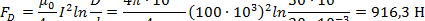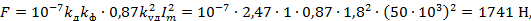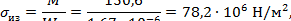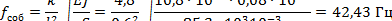Электродинамической стойкостью аппарата называют его способность противостоять без повреждений и нарушений функционального состояния механическим силам, возникающим при протекании токов.
Электродинамическая стойкость количественно характеризуется током электродинамической стойкости (наибольшим значением тока, который аппарат может выдержать во включенном состоянии без механических или электрических повреждений и без произвольного отключения). Ток электродинамической стойкости электрического аппарата должен быть больше ударного тока короткого замыкания для данных условий работы. Электродинамическая стойкость выражается либо амплитудным значением тока, при котором механические напряжения в элементах аппарата не выходят за пределы допустимых величин, либо кратностью тока относительно амплитуды номинального тока.
При оценке электродинамической стойкости необходимо учитывать степень защиты аппарата, так как для аппаратов открытого исполнения существуют дополнительные нагрузки от воздействия внешних факторов. В этом случае результирующая нагрузка на изоляторы и изоляционные детали берется в 3 раза меньше разрушающей, для аппаратов герметичного исполнения – в 1,5–1,7 раза. В случае, когда частота переменной составляющей электродинамической силы близка к собственной частоте механических колебаний, даже при сравнительно небольших силах возможно разрушение аппарата вследствие явлений резонанса. Возможность резонанса стремятся исключить.
Примеры решения задач
Пример 1. Определить электродинамическое усилие, действующее на 1 м длины прямолинейного бесконечно тонкого проводника, по которому протекает постоянный ток I = 10 кА. Проводник находится в однородном постоянном магнитном поле, магнитная индукция в каждой точке проводника B = 0,1 Тл, а угол между направлением тока и вектором индукции b = 30°.
Решение. Действующее на проводник усилие определяется на основе закона Ампера [формула (48)]:
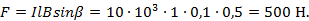
|
Ответ: F = 500 Н.
Пример 2. Определить величину электродинамического усилия, с которым притягиваются друг к другу два параллельных круглых, бесконечно длинных проводника, находящихся на расстоянии одного метра друг от друга (a = 1 м). Токи в проводниках равны 10 и 20 кА.
Решение. Электродинамическое усилие, действующее между параллельными проводниками, определим по формуле (50):
|
| |||
| где | 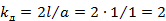
| ‒ | коэффициент электродинамических сил для бесконечно длинных проводников. |
Пример 3. Определить электродинамическое усилие, действующее между параллельно расположенными шинами (рис. 23), если I1 =10 кА, I2 =15 кА, l1 =1 м, l2 =1,5 м, a = 0,5 м.
Решение. Электродинамическое усилие, действующее между параллельными проводниками, определим по выражению (50)
|
| |||
| где | 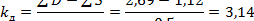
| ‒ | коэффициент электродинамических сил для двух параллельных проводников разной длины. |
Ответ: F = 47,1 Н.
Пример 4. Определить усилие, разрывающее проводник с током I = 100 кА в месте, где проводник изменяет свое поперечное сечение от D = 50 мм до d = 20 мм.
Решение. Электродинамическое усилие в проводниках при изменении поперечного сечения (усилие Дуайта)
|
| |||
| где | μ0 = 4π ∙ 10-7 Гн/м | ‒ | магнитная проницаемость вакуума. |
Ответ: FD = 916,3 Н.
Пример 5. Определить электродинамическое усилие, возникающее между двумя витками цилиндрического однослойного реактора, имеющего радиус витка R = 1 м. Витки имеют шаг h = 10 мм. По реактору протекает ток короткого замыкания I = 50 кА.
Решение. Для решения воспользуемся формулой (56):

|
Ответ: Fh = 314000 Н.
Пример 6. Определить:
1) электродинамическую силу, возникающую между двумя витками цилиндрического однослойного реактора, имеющего радиус R = 1 м;
2) силу в витках реактора
3) силу, разрывающую виток, изготовленный из круглого провода радиусом r = 10 мм. Шаг витков реактора h = 20 мм. По реактору протекает ток короткого замыкания Iкз = 50 кА.
Решение. Для решения задачи можно воспользоваться формулами энергетического баланса F = 𝜕 W / 𝜕 x, определения энергии 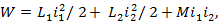 взаимной индуктивности
взаимной индуктивности 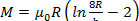 и индуктивности
и индуктивности 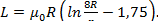
Электродинамическая сила, действующая между витками реактора, определяется по формуле

|
Тогда
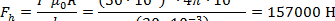
|
Электродинамическая сила в витке, обусловленная собственной индуктивностью, определяется по формуле
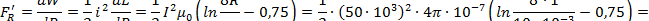
|
| = 9317 Н. |
Электродинамическая сила в витке, обусловленная взаимодействием тока витка с продольной составляющей тока другого витка, определяется по формуле
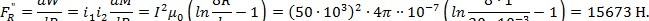
|
Сила в витке реактора
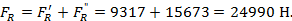
|
Эта сила равномерно распределена по дуге окружности витка.
Сила, разрывающая виток,
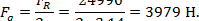
|
Ответ: Fh =157000 Н; FR = 24990 Н; Fq = 3979 Н.
Пример 7. Проверить, удовлетворяют ли условиям прочности и жесткости ножи трехполюсного разъединителя (рис. 26), по которым протекает предельный ток трехфазного короткого замыкания. Амплитуда установившегося тока короткого замыкания Iкз = 50 кА, частота тока f = 50 Гц.
Ножи разъединителя выполнены из меди, поперечное сечение их имеет прямоугольную форму с размерами h х b =100 х 10 мм. Ножи расположены широкими сторонами друг к другу, жестко закреплены в нижней части разъединителя и свободно опираются в верхней части.
Длина ножей l = 600 мм, расстояние между ними a = 300 мм.
| |
| Рис. 26. Эскиз разъединителя |
Решение. С электрической точки зрения ножи разъединителя представляют собой токоведущие прямолинейные проводники, с механической точки зрения – балку на двух опорах.
Максимальная сила возникает в средней фазе. При наличии апериодической составляющей тока эта сила определяется по формуле
|
| |
| где | 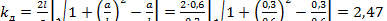 ‒ геометрический фактор, k ф ~ 1 при ‒ геометрический фактор, k ф ~ 1 при 
|
Нож разъединителя можно рассчитать как балку на двух опорах, при этом напряжение на изгиб
|
| |
| где | 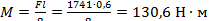 ‒ максимальное значение изгибающего момента; ‒ максимальное значение изгибающего момента;
|
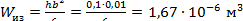 ‒ момент сопротивления. ‒ момент сопротивления.
| |
Напряжение на изгиб меньше допустимого напряжения для меди (σиз = 78,2 ∙106 Н/м2 <= σдоп =137 ∙106 Н/м2), следовательно, ножи рубильника удовлетворяют условиям прочности.
Во избежание появления механического резонанса необходимо, чтобы частота собственных колебаний механической системы не была равна частоте силы.
Для параллельных шин частота собственных колебаний
|
| |
| где | k – коэффициент, учитывающий жесткость заделки ножа. При жестко заделанном одном конце и свободном закреплении другого конца k = 4,8; |
| E = 10,8 ∙1010 Н / м2 – модуль упругости меди; | |
| γ = 85,3 ∙ 103 Н / м3 – удельный вес меди; | |
| S = h ∙ b =0,1 ∙ 0,01=10-3 м2 ‒ площадь поперечного сечения; | |
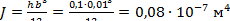 ‒ момент инерции поперечного сечения. ‒ момент инерции поперечного сечения.
| |
Так как собственная частота меньше вынужденной (fсоб = 42,43 Гц < fд =100 Гц), механический резонанс не будет иметь места, а ножи удовлетворяют условиям жесткости.
Ответ: Ножи разъединителя удовлетворяют условиям прочности и жесткости.
Дата: 2019-02-25, просмотров: 557.