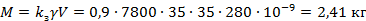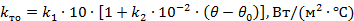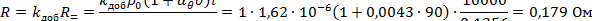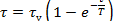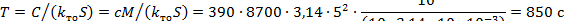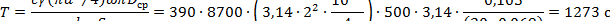Так как время действия токов короткого замыкания значительно меньше постоянной времени нагрева токоведущих частей (tкз < 0,05T), процесс нагрева является адиабатическим (тепло не отдается в окружающую среду, а все идет на нагрев).
Уравнение теплового баланса преобразуется к виду
|
| (46) | |||
| где | j | ‒ | плотность тока; | |
| c | ‒ | удельная теплоемкость; | ||
| γ | ‒ | плотность материала проводника; | ||
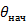
| ‒ | начальная температура; | ||
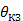
| ‒ | температура в конце короткого замыкания. | ||
По известной зависимости удельной теплоемкости, плотности и удельного сопротивления от температуры для некоторых широко распространенных материалов (сталь, алюминий, медь) построены графики B(Θкз), которые позволяют определить температуру в конце процесса короткого замыкания. При этом значение интеграла
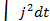
|
может быть определено по кривой изменения тока короткого замыкания во времени либо другими методами (например, заменой реального процесса короткого замыкания некоторым фиктивным, эквивалентным реальному по тепловому действию). С помощью кривых B(Θкз) можно определить допустимую плотность тока в проводнике либо длительность процесса короткого замыкания при известной допустимой температуре. Допустимые температуры в конце короткого замыкания: для медных неизолированных проводников или проводников с изоляцией органического происхождения – 250 °С, для медных проводников с неорганической изоляцией – 350 °С, для алюминиевых проводников – 200 °С.
Токоведущие элементы аппарата, рассчитанные для длительного режима, должны быть проверены на термическую стойкость при коротком замыкании.
Термической стойкостью электрического аппарата называют его способность выдерживать кратковременное тепловое действие токов короткого замыкания без повреждений. Термическая стойкость количественно оценивается током термической стойкости.
При расчете берется наиболее тяжелый случай – к моменту начала короткого замыкания элемент нагрет длительным током до предельно допустимой температуры номинального режима.
Термическая стойкость аппарата и его токоведущих частей определяется действующим значением тока термической стойкости, протекание которого в течение времени термической стойкости (1, 3, 5 и 10 секунд) не вызывает нагрева выше допустимых температур. Связь между токами термической стойкости для различных времен выражается равенством
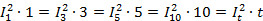
| (47) |
Примеры решения задач
Пример 1. Определить коэффициент поверхностного эффекта для алюминиевого шинопровода, нагретого протекающим по нему переменным током промышленной частоты до температуры Θ = 95 °С, для следующих случаев:
а) шинопровод круглый d = 80 мм;
б) шинопровод трубчатый с наружным диаметром нар d = 80 мм, внутренним диаметром d вн = 50 мм;
в) шинопровод трубчатый с наружным диаметром нар d = 80 мм, внутренним диаметром d вн = 74 мм.
Решение. Коэффициент поверхностного эффекта можно определить по графикам, изображенным на рис. П.1 и П.2. Для этого вычисляется величина f / R 100, где f – частота переменного тока, Гц; R 100 – активное сопротивление постоянному току проводника длиной l =100 м, Ом.
Для условия (а) рассматриваемой задачи
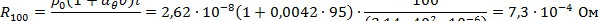
|
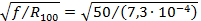 = 262 Гц0,5/Ом0,5 = 262 Гц0,5/Ом0,5
|
Коэффициент поверхностного эффекта kп = 1,8 (рис. П.1).
Для условия (б) задачи
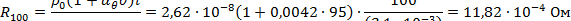
|
где 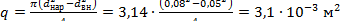 ‒ сечение трубчатого шинопровода;
‒ сечение трубчатого шинопровода;
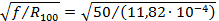 = 205,7 Гц0,5/Ом0,5 = 205,7 Гц0,5/Ом0,5
|
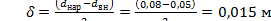 ‒ толщина стенки трубы;
‒ толщина стенки трубы;
D = d нар; δ/ D = 0,015 / 0,08 = 0,1875.
Коэффициент поверхностного эффекта kп = 1,1 (рис. П.2).
Для условия (в) задачи
|
| |
| где | 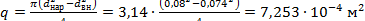 ‒ сечение трубчатого шинопровода; ‒ сечение трубчатого шинопровода;
|
|
| |
|
| |
| D = d нар; δ/ D = 0,003 / 0,08 = 0,0375. | |
Коэффициент поверхностного эффекта k п = 1,02 (рис. П.2).
Ответ: а) k п = 1,75; б) k п = 1,1; в) k п = 1,02.
Пример 2. Определить мощность потерь в магнитопроводе, выполненном из трансформаторной листовой стали марки 1511 с толщиной листа Δ = 0,35 мм, если по катушке, имеющей число витков ω =1250, протекает переменный ток I = 0,6 А частотой f = 50 Гц. Размеры магнитопровода приведены на рис. 20.
Решение. Определим массу стали магнитопровода с учетом коэффициента заполнения поперечного сечения сталью kз = 0,9:
|
| |
| где | γ = 7800 кг/м3 ‒ плотность стали (табл. П.4); |
| V ‒ объем стали. | |
Напряженность магнитного поля
|
| |
| где | l ср = 280 ∙ 10-3 м ‒ средняя длина магнитной силовой линии (рис. 20). |
| |
| Рис. 20. Эскиз магнитопровода с катушкой |
Значение индукции B =1,46 Тл для H = 2700 А/м; удельные тепловые потери pуд = 3 Вт/кг (табл. П.4).
Потери в сердечнике
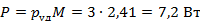
|
Ответ: P = 7,2 Вт.
Пример 3. Рассчитать значение установившейся температуры медного круглого окрашенного краской проводника диаметром d = 25 мм, по которому протекает постоянный ток I =1000 А. Температура окружающего воздуха Θо = 35 °С.
Решение. Исходным уравнением для решения задачи является уравнение (41):
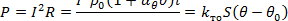
|
Коэффициент теплоотдачи (табл. 6)
|
| |
| где | 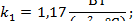
|
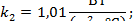
| |
Принимаем расчетную длину шины равной 1 метру и подставляем числовые значения в исходное уравнение:
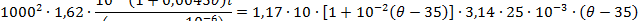
|
Решая последнее (квадратное) уравнение, находим Θ = 70 oС.
Ответ: Θ = 70 oС.
Пример 4. Определить длительно допустимую величину плотности переменного тока частотой 50 Гц катушки электромагнита. Катушка намотана медным круглым проводом, диаметр которого d = 4 мм; изоляция хлопчатобумажная, без пропитки. Число витков катушки ω = 250, высота катушки H =170 мм, внутренний и наружный диаметры катушки D вн =100 мм и D нар =155 мм соответственно (рис. 21). Катушка находится в спокойном воздухе при Θо = 35 oC.
| |
| Рис. 21. Эскиз катушки |
Решение. Для решения задачи воспользуемся формулами Ньютона P = k то S(Θ - Θ 0), расчета мощности потерь – P = I 2 R, сопротивления на переменном токе – R ∼ = k п R = и сопротивления на постоянном токе – R = = rl / q.
Коэффициент теплоотдачи для цилиндрических катушек при площади поверхности охлаждения 100 < S < 5000 cм2 [2].
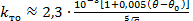 = 2,3 ∙ 10-3 ∙ = 2,3 ∙ 10-3 ∙ 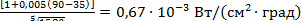
|
где площадь поверхности охлаждения
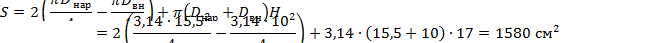
|
допустимая температура для данного класса изоляции Θдоп = 90 oС (табл. П.2).
Допустимый длительный ток определяется из равенства выделяемой и отводимой с поверхности мощности потерь P = k то S (Θ – Θ0) = I 2 R:
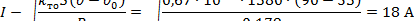
|
Здесь активное сопротивление
|
| |
| где | 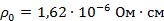 ‒ удельное сопротивление проводника при 0 oС; ‒ удельное сопротивление проводника при 0 oС;
|
 ‒ температурный коэффициент сопротивления; ‒ температурный коэффициент сопротивления;
| |
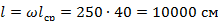 ‒ длина проводников катушки; ‒ длина проводников катушки;
| |
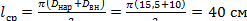 ‒ средняя длина витка катушки; ‒ средняя длина витка катушки;
| |
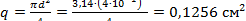 ‒ площадь поперечного сечения провода. ‒ площадь поперечного сечения провода.
| |
Допустимая плотность тока в катушке
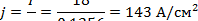
|
Ответ: j =143 А/см2.
Пример 5. Написать уравнение кривой нагрева круглого медного проводника диаметром d =10 мм, по которому протекает постоянный ток I = 400 А, если коэффициент отдачи с поверхности проводника kто =10 Вт/(м2×oС), температура окружающей среды, которой является спокойный воздух, Θо = 35 oС. Значение удельного сопротивления меди за время нарастания температуры ρ = 1,75 ∙ 10-8 Ом ∙ м.
Решение. Уравнение кривой нагрева
|
| |
| где | 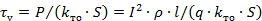 ‒ установившееся превышение температуры. ‒ установившееся превышение температуры.
|
Расчет проведем для проводника длиной l = 1 м:
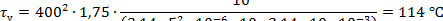
|
Постоянная времени нагрева
|
| |||
| где | c | ‒ | удельная теплоемкость меди; |
| M = γV | ‒ | масса проводника длиной в 1 м; | |
| γ | – | плотность меди; | |
| V | – | объем проводника. | |
Уравнение кривой нагрева
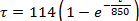
|
Ответ: τ = 114(1 ‒ e(-t/850) )
Пример 6. Определить допустимое число включений n в час катушки постоянного тока в повторно-кратковременном режиме нагрева, если время работы катушки раб t =150 с и по ней протекает допустимый ток повторно-кратковременного режима работы Iп.кр =12 А.
Цилиндрическая катушка, намотана круглым проводником, диаметр которого d = 2 мм, число витков катушки ω = 500, внутренний диаметр катушки Dвн = 70 мм, наружный диаметр катушки Dнар =140 мм, высота катушки равна H = 70 мм. Катушка находится в спокойном воздухе, температура которого Θо = 35 oС. Коэффициент теплоотдачи kто = 20 Вт/(м2 ∙ oС). Изоляция проводника – хлопчатобумажная, без пропитки.
Решение. Длительно допустимая величина тока определяется из равенства
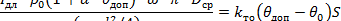
|
Для хлопчатобумажной изоляции допустимая температура Θ доп = 90 oС.
Ток длительного режима
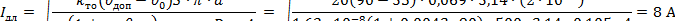
|
где средний диаметр катушки
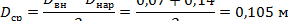
|
площадь поверхности охлаждения
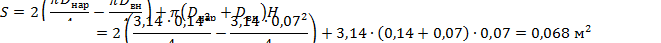
|
Коэффициент перегрузки по току
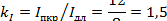
|
Постоянную времени нагрева катушки определим из условия, что способностью воспринимать теплоту обладают только токопроводящие элементы:
|
| |||
| где | c | ‒ | удельная теплоемкость меди; |
| γ | ‒ | плотность меди. | |
Подставив в равенство
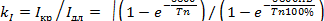
|
выражение для 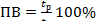 и
и 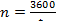 , получим
, получим
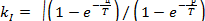
|
Из последнего уравнения определим время цикла
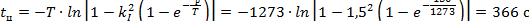
|
Допустимое число включений катушки в час n = 3600/tц = 3600/366 = 9,8 ~ 9.
Ответ: n = 9.
Электродинамические силы
Дата: 2019-02-25, просмотров: 544.
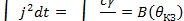
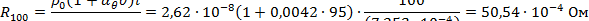
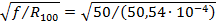 = 99,5 Гц0,5/Ом0,5
= 99,5 Гц0,5/Ом0,5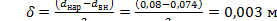 ‒ толщина стенки трубы;
‒ толщина стенки трубы;