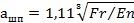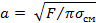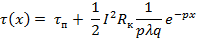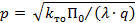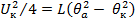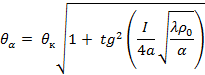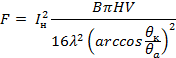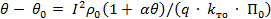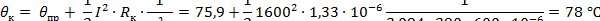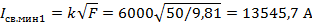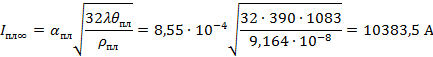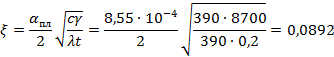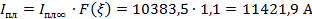Для удобства чтения схем вводятся условные графические обозначения аппаратов и их элементов.
Существуют также сокращенные условные обозначения аппаратов, например, ВЭ-10-1250-20-У3 (выключатель электромагнитный, напряжение 10 кВ, номинальный ток 1250 А, номинальный ток отключения 20 кА, предназначен для эксплуатации в зоне умеренного климата в закрытых помещениях).
ОСНОВЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ АППАРАТОВ
Контакты электрических аппаратов
Понятие контакт
Электрические контакты предназначены для соединения элементов электрической цепи.
Электрический контакт можно рассматривать как место перехода тока из одного токоведущего элемента в другой. Соприкасающиеся (контактирующие) проводники называют контактами, или контакт ‒ деталями.
В замкнутом положении контакты электрических аппаратов сжаты с определенной силой, создаваемой контактными пружинами.
По назначению контакты делятся на соединительные (неразмыкаемые), которые служат только для проведения тока и всегда замкнуты, и коммутирующие, которые дополнительно служат для включения, отключения и переключения электрических цепей.
Коммутирующие контакты в сильноточных аппаратах можно разделить на главные (токоведущие) и дугогасительные. Главные шунтируются дугогасительными, поэтому образование дуги происходит на дугогасительных контактах и главные оказываются защищенными от воздействия дуги. Часто одни и те же контакты выполняют роль и главных, и дугогасительных.
Слаботочные контакты используются в реле защиты и автоматики и комму-тируют токи до 5 А при напряжении в десятки и сотни вольт. Контакты аппаратов управления коммутируют токи в нормальном режиме до 1 кВ. Сильноточные контакты используются для коммутации токов в десятки тысяч ампер при напряжении до сотен тысяч вольт.
Конструкции контактов
По конструктивному исполнению соединительные контакты могут быть неподвижными и подвижными.
Неподвижные контакты могут быть неразъемными, например, сварными (рис. 1) и разъемными, например, болтовыми (рис. 2).
| | |
| Рис. 1. Сварной контакт | Рис. 2. Болтовой контакт |
Различают следующие типы подвижных контактов: скользящие щеточные, роликовые, жидкометаллические.
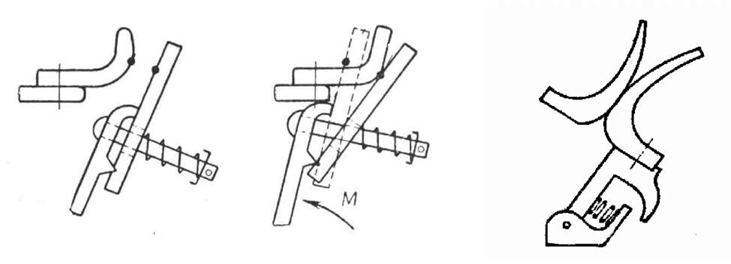
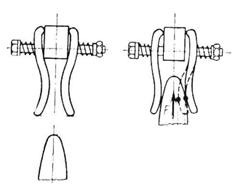
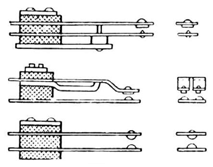
Коммутирующие контакты могут быть рычажными (рис. 3), рубящими, торцовыми, щеточными, пальцевыми (рис. 4), розеточными, с плоскими пружинами для реле (рис. 5) и т.д.
|
| Рис. 3. Рычажные контакты |
| 
|
| Рис. 4. Пальцевые контакты | Рис. 5. Контакты с плоскими пружинами |
2.1.3 Сопротивление контакта
Сопротивление контакта (переходное сопротивление) R к складывается из сопротивления стягивания R с и сопротивления пленок R пл:
| R к = R с + Rпл | (1) |
Сопротивление стягивания обусловлено стягиванием линий тока к местам истинного касания контактирующих проводников (рис. 6) и зависит от материала и обработки контактирующих проводников, числа площадок касания, силы сжатия.
Сопротивление пленок обусловлено загрязнением или окислением поверхностей контактирующих проводников и может меняться в процессе эксплуатации. Возникновение пленок на поверхности контактов зависит от материала контактов, температуры среды, в которой находятся контакты.
Борьба с пленками ведется конструктивными мерами. Конструкции контактов выполняют таким образом, чтобы при размыкании или замыкании они разрушали пленку. В соединительных контактах защита от образования оксидных пленок осуществляется с помощью специальных смазок.
Пленки особенно опасны при малых токах, так как в этом случае сопротивления Rс и Rпл соизмеримы. В связи с этим контакты на малые токи изготовляются из благородных материалов (золото, платина и др.), менее подверженных образованию пленок.
Положительная роль оксидных пленок заключается в том, что они не дают возможности развиваться чрезмерно большим силам межмолекулярного сцепления на поверхности касания контактов.
Для расчета сопротивления стягивания разработаны различные упрощающие модели контактировния. В одной из простейших моделей Хольма площадка касания представляет собой круг радиуса а.
Сопротивление стягивания при этом определяется выражением
| R с = ρ / (2nа) | (2) | |||
| где | ρ | ‒ | удельное электрическое сопротивление материала контактов; | |
| n | ‒ | число одинаковых площадок касания. | ||
Радиус площадки касания в случае упругой деформации:
• при сжатии контактов силой F гладких поверхностей шар ‒ плоскость из одинаковых материалов определяется формулой Герца
|
| (3) | |||
| где | r | ‒ | радиус шара; | |
| E | ‒ | модуль упругости; | ||
• при сжатии двух одинаковых шаровых поверхностей ‒ выражением
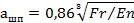
| (4) |
Если деформация при сжатии контактов носит пластический характер, то радиус площадки касания определяется как
|
| (5) | |||
| где | σсм | ‒ | временное сопротивление смятия материала контактов | |
Для практических расчетов сопротивления контакта часто используют эмпирическую формулу
| Rк = Kо / F m | (6) |
Значения коэффициента K0 приводятся в справочных таблицах (табл. 3). Показатель степени m принимается равным:
для точечного контакта (n = 1) ‒ 0,5;
для линейного (n = 2) ‒ 0,5-0,8;
для плоскостного (n > 3) ‒ 1.
Таблица 3 ‒ Коэффициент K0 для расчета сопротивления контакта
| Материал контактов | Тип контакта | Условия | Значения K0 , мкОм • Н m |
| Медь - медь | Сильноточные | 400 | |
| Латунь - сталь | Сильноточные | 3 ∙ 103 | |
| Медь - медь | Плоскостной | Слаботочные | (90 - 280) ∙ 103 |
| Медь - медь | Точечный | Слаботочные | (140 -170) ∙ 103 |
| Медь - медь | Щеточный | Слаботочные | 100 ∙ 103 |
С ростом силы сжатия F сопротивление контакта уменьшается (кривая 1, рис. 7). При уменьшении силы сжатия (кривая 2) зависимость Rc ( F ) идет ниже из-за наличия остаточных деформаций контактирующих выступов.
| |
| Рис. 6. Стягивание линий тока в контакте | Рис. 7. Характеристика переходного сопротивления |
Сопротивление контакта не остается постоянным в эксплуатации из-за действия электрического поля и температуры. Обычно экспериментальные исследования и расчет переходного сопротивления ведутся для свеже зачищенных контактов.
Нагрев контакта
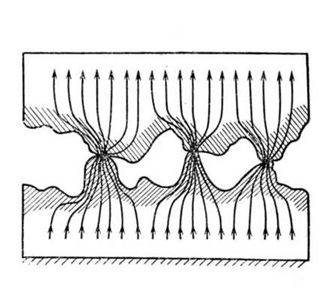
В контактном соединении можно выделить зону стягивания, протяженность которой невелика и в которой сосредоточено переходное сопротивление. Теплота, генерируемая в этой зоне, распространяется от площадки касания в части проводников, прилегающие к ней, только за счет теплопроводности, а затем ‒ в окружающую среду. На рис. 8 изображена картина распространения теплоты в симметричном контактном соединении.
Кривая распределения превышения температуры вдоль проводника с контактом изображена на рис. 9. Наибольшую температуру имеет площадка касания. По мере удаления от нее температура быстро падает.
| | |
| Рис. 8. Распространение теплоты в контактном соединении | Рис. 9. Распределение температуры в контакте |
Уравнение распределения превышения температуры вдоль проводника выглядит следующим образом.
|
| (7) | |||
| где | τn | ‒ | превышение температуры проводника над температурой окружающей среды при x → ∞; | |
|
| ||||
| k то | ‒ | коэффициент теплоотдачи с боковой поверхности проводника; | ||
| П0 | ‒ | периметр боковой поверхности проводника; | ||
| λ | ‒ | теплопроводность проводника; | ||
| q | ‒ | площадь поперечного сечения проводника. | ||
Превышение температуры тела контакта (превышение температуры границы области стягивания x = 0).
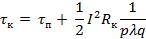
| (8) |
Если расстояние между двумя соседними контактами удовлетворяет условию 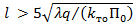 , то взаимным тепловым влиянием контактов можно пренебречь.
, то взаимным тепловым влиянием контактов можно пренебречь.
На основании теоремы Кольрауша и Диссельхорста для идеализированной модели контактирования (в симметричной области стягивания все эквипотенциальные поверхности являются изотермическими) выводится уравнение, связывающее падение напряжения на контакте U к с температурой площадки касания Θа
|
| (9) | |||
| где | Θк | ‒ | температура на границе зоны стягивания (x = 0); | |
| L | ‒ | постоянная, для большинства металлов близкая к L = 24 ∙ 10-8, В2К-2 | ||
Температура площадки касания связана с температурой тела контакта:
|
| (10) | |||
| где | a | ‒ | температурный коэффициент сопротивления | |
Из уравнения (9) следует, что для данного материала существуют определенные падения напряжения на контакте, при которых температура площадки касания достигает значений, определяющих фазовое состояние материала (размягчения, плавления, кипения, табл. 4).
Таблица 4 ‒ Напряжения размягчения и плавления
| Материал | Напряжение размягчения, В | Напряжение плавления, В |
| Серебро | 0,09 | 0,37 |
| Медь | 0,12 | 0,43 |
| Никель | 0,22 | 0,65 |
| Платина | 0,25 | 0,65 |
| Вольфрам | 0,40 | 1,10 |
Для слаботочных контактов принимают, что допустимое падение напряжения не должно превосходить напряжения размягчения 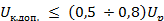 .
.
Если известен ток I, который должны пропускать контакты, то можно найти допустимое сопротивление контакта
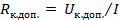
| (11) |
При выбранном материале контактов знание сопротивления контактов позволяет отыскать необходимую силу сжатия контактов.
Расчет одноточечных контактов на большие токи ведется по выражению
|
| (12) | |||
| где | I н | ‒ | номинальный ток; | |
| F | ‒ | сила контактного нажатия; | ||
| HV | ‒ | твердость по Виккерсу; | ||
| B | ‒ | число Лоренца. | ||
Токи короткого замыкания и длительные токи перегрузки могут привести к расплавлению материала контактов и их свариванию.
Минимальный плавящий ток определяется выражением.
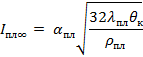
| (13) |
В этом выражении все величины должны быть взяты при температуре плавления. Размеры площадки касания при температуре плавления a пл = 1,5a.
Минимальный плавящий ток, с учетом изменения температуры во времени,
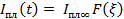
| (14) |
где функция F(ξ) выбирается в зависимости от 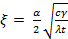 (рис. 10), c ‒ удельная теплоемкость материала; γ ‒ плотность материала.
(рис. 10), c ‒ удельная теплоемкость материала; γ ‒ плотность материала.
|
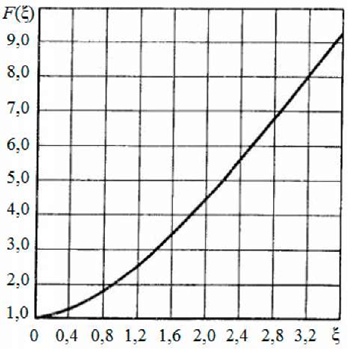
| Рис. 10. График функции F(ξ) |
При практических расчетах используют эмпирическую зависимость между минимальным током сваривания I св мин и силой сжатия контактов
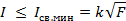
| (15) |
Коэффициент k зависит от свойств материала и конструкции контактов (табл. 5).
Таблица 5 ‒ Коэффициент k для расчета тока сваривания
| Тип контакта | Материал | k , А/кг0,5 |
| Щеточный | Медь - латунь | 3000-4000 |
| Пальцевый несамоустанавливающийся | Медь - медь. | 4100 |
| Латунь - латунь | 5050 | |
| Пальцевый самоустанавливающийся | Медь - латунь | 5750 |
| Розеточный (на 1 элемент розетки) | Медь - латунь. | 5500 |
| Медь - медь | 6000 |
Для медных и латунных контактов по опытным данным величина k = 1000 - 2000 А/Н1/2.
2.1.5 Режимы работы контактов
Условия работы контактов определяются их возможными состояниями (контакты замкнуты или разомкнуты).
Замкнутое состояние характеризуется протеканием номинальных и аварийных токов, а также процессами нагрева контактов.
Разомкнутое состояние характеризуется максимальным напряжением, которое выдерживает изоляционный межконтактный промежуток без пробоя. Напряжение пробоя межконтактного промежутка в целях надежности должно быть выше максимального напряжения при разомкнутых контактах. Расстояние между ближайшими точками контакт-деталей в разомкнутом состоянии называется раствором контактов. Раствор контактов выбирается из условий электрической прочности межконтактного промежутка и гашения дуги. Установлены соответствующие испытательные напряжения, воздействие которых должны выдерживать межконтактные промежутки.
Работоспособность коммутирующих контактов характеризуется также процессами замыкания (включения) и размыкания (отключения) цепи.
Включение цепи. При включении электрических аппаратов в их контактах могут иметь место следующие процессы: вибрации, эрозия на поверхности контактов в результате образования электрического разряда между ними. При достижении некоторого расстояния между контактами создаются условия для электрического пробоя, в результате которого между электродами загорается дуга замыкания. При соприкосновении контактов дуга гаснет. Если соприкосновение контактов носит ударный характер, то возможен неоднократный отброс подвижного контакта (вибрация). Не исключено повторное возникновение дуги или искры, которые ведут к износу контактов.
Отключение цепи. В процессе размыкания сила сжатия контактов уменьшается, переходное сопротивление увеличивается, за счет чего растет температура площадок касания. В момент разъединения контакты нагреваются до температуры плавления и между ними возникает мостик из жидкого металла. При дальнейшем движении контактов мостик обрывается и, в зависимости от параметров отключаемой цепи, возникает дуговой или тлеющий разряд. Разрыв жидкометаллического мостика, проскакивание искры или горение дуги являются причинами износа контактов (электрической эрозии). Высокая температура приводит к интенсивному окислению и распылению материала контактов в окружающем пространстве, переносу материала с одного электрода на другой и образованию пленок. Перенос материала с одного контакта на другой наиболее вреден при постоянном токе, так как направление переноса в этом случае постоянно. Эрозия контактов под действием малых токов определяется мостиковой стадией и стадией искрового разряда. Для уменьшения эрозии применяются искрогасительные схемы. Для борьбы с эрозией контактов сокращают длительность горения дуги с помощью дугогасительных устройств, устраняют вибрации контактов при включении, применяют дугостойкие материалы контактов.
2.1.6 Материалы контактов
Материалы контактов должны иметь высокие электрическую проводимость и теплопроводность, стойкость против образования пленок и коррозии, малую твердость для уменьшения силы сжатия, высокую твердость для уменьшения механического износа, малую эрозию, высокую дугостойкость, простоту обработки, низкую стоимость.
В качестве материалов контактов используют: чистые металлы (медь, алюминий, серебро, вольфрам и др.), сплавы (латунь, бронза и др.), неметаллы (углерод), композиции взаимно не сплавляемых металлов (вольфрам-серебро, вольфрам-медь), композиции металлов с оксидами металлов (серебро ‒ оксид кадмия, серебро ‒ оксид меди, медь ‒ оксид меди), композиции металлов с карбидами (вольфрам ‒ карбид вольфрама), композиции металлов с углеродом (серебро ‒ графит, медь ‒ графит) и многочисленные тройные композиции. Выбор материала контактов определяется условиями их работы.
2.1.7 Примеры решения задач
Пример 1. Два круглых медных стержня на торцах обработаны под сферу г = 40 мм и стянуты силой F = 100 Н. Определить сопротивление стягивания R.
Решение. Найдём радиус площади касания при условии, что имеет место упругая деформация [выражение (4)]
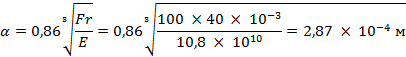
где E = 10,8 ∙ 1010 H/м - модуль упругости меди (табл. П.1).
Механическое напряжение в контактной площадке
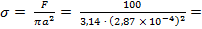 38,7 ∙ 107 Н/м2.
38,7 ∙ 107 Н/м2.
Это напряжение больше, чем напряжение смятия меди 7 2 σсм = 38,3 ∙ 107 Н/м2, и, следовательно, будет иметь место пластическая деформация.
Радиус площадки касания при пластической деформации определим по формуле (5)
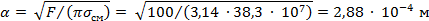
|
Сопротивление стягивания будет равно
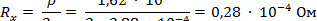
|
где ρ= 1,62 ∙ 10-8 Ом ∙ м ‒ удельное сопротивление меди (табл. П.1).
Ответ: R = 0,28 10-4 Ом.
Пример 2. Определить величину F контактного нажатия мостикового контакта, если через контакт протекает ток I = 5 А, а контакты изготовлены из серебряных накладок полусферической формы радиуса г = 1 см.
Решение. Для надежной работы контактов необходимо, чтобы падение напряжения на них было меньше напряжения размягчения U к.доп < (0,5 ‒ 0,8)U разм .
Примем, что U к.доп = 0,5U разм (по табл. 4 для серебра U разм = 0,09 В).
Допустимое сопротивление контактов
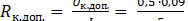 =9 ∙ 10-3 Ом =9 ∙ 10-3 Ом
|
Определим радиус площадки касания по формуле (2)
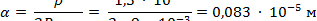
|
где ρ = 1,5 ∙ 10-8 Ом ∙ м ‒ удельное сопротивление серебра.
В случае упругой деформации при контактировании двух сферических поверхностей радиус площади касания [выражение (4)]
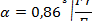
|
откуда сила нажатия на один контакт
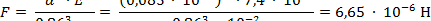
|
где E = 7,4 ∙ 1010 H/м2 ‒ модуль упругости серебра.
Так как мостик имеет два контакта, суммарная сила контактов
F = 2 ∙ F = 2 ∙ 6,65 10-6 = 13,3 ∙ 10-6 Н.
Ответ: Fк = 13,3 ∙ 10-6 Н.
Пример 3. Определить температуру контакта, выполненного в виде двух плоских медных шин размером 60х10 мм, составленных встык и сжатых силой F = 300 Н. Через контакт протекает ток I = 1600 А, шины находятся в воздухе, температура которого Θ0 = 35 оC, коэффициент теплоотдачи с поверхностей шин k то = 16 Вт/(м2 ∙ °C). Шины бесконечно длинные.
Решение. Определим установившееся значение температуры шины в точках, удаленных от места контактирования, по закону Ньютона (разд. 2.3.4):
|
| |||
| где | 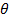
| ‒ | температура тела, °С; |
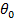
| – | температура окружающей среды, °С; | |
| a | ‒ | температурный коэффициент меди, a = 0,0043 1/°С; | |
| q | – | сечение проводника, q = 600 мм2; | |
| П0 | – | периметр проводника, П0 = 2 ∙ (60 +10) =140 мм. | |
Получим температуру проводника
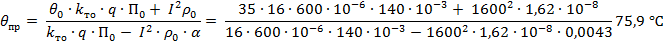
|
Температура контакта, в соответствии с уравнением (7),
|
| |
| где | 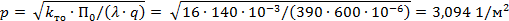
|
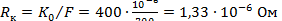 ‒ сопротивление плоскостного контакта, рассчитанное по эмпирической формуле (6); ‒ сопротивление плоскостного контакта, рассчитанное по эмпирической формуле (6);
| |
| λ = 390 Вт/(м ∙ oC) ‒ теплопроводность меди. | |
Ответ: Θк = 78 °С.
Пример 4. Определить минимальный сваривающий ток розеточного контакта из меди, если сила F = 50 Н на одну ламель, всего ламелей 6 штук.
Решение. В практических расчетах можно воспользоваться формулой Буткевича, которая непосредственно связывает минимальный сваривающий ток и силу контактного нажатия. Для одной ламели по выражению (15)
|
| |||
| где | k | ‒ | коэффициент, выбираемый из справочника по типу контакта и материалу, из которого сделан контакт (табл. 5), k = 6000 А/кг0,5. |
Для всего контакта
I св.мин6 = 6 ∙ 13545,7 = 81274 А.
Ответ: I св.мин6 = 81274 А
Пример 5. Два медных стержня диаметром d = 20 мм сжаты силой F = 390 Н. Торцы обработаны под сферу r = 10 мм. Определить, какой постоянный ток в течение времени t = 0,2 с контакты выдержат без сваривания.
Решение. Минимальный плавящий ток можно определить по формуле (13):
|
| |||
| где | θпл | ‒ | температура плавления меди, oC, 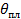 = 1083 oC; = 1083 oC;
|
| ρпл | ‒ | удельное сопротивление меди при температуре плавления, Ом·м, | |
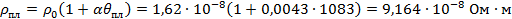 ; ;
| |||
| α | ‒ | радиус площадки касания (при температуре плавления радиус площадки касания | |
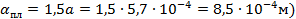 , ,
| |||
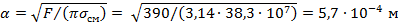 . .
| |||
Изменение температуры во времени определяется безразмерным комплексом ξ:
|
| |||
| где | c | ‒ | удельная теплоемкость меди, Дж/(кг ∙ оС), c = 390 Дж/(кг ∙ оС); |
| g | ‒ | плотность меди, g = 8700 кг/м3. | |
Ток, плавящий площадку за время t по формуле (14),
|
| |||
| где | F(ξ) | ‒ | функция, определяемая по графику (рис. 10), F ( ξ ) = 1,1. |
Ответ: I пл = 11421,9 А.
2.2 Электрическая дуга и дугогашение
2.2.1 Понятие электрическая дуга
Электрическая дуга является одним из видов газового разряда (явление прохождения тока через газ).
Дуга (дуговой разряд) возникает при размыкании (замыкании) электрических цепей с помощью контактов электрических аппаратов (выключателей, автоматов, контакторов, пускателей, рубильников, реле), если величины токов и напряжений превосходят некоторые критические значения. Эти значения зависят от материала контактов, пара метров цепи, свойств среды и т.д. Дуговой разряд имеет место при относительно больших токах (для металлов ‒ примерно 0,5 А) и при напряжении в цепи не менее 15 В. При меньших значениях тока и напряжения размыкание контактов сопровождается образованием искр.
Дуговой разряд в газовой среде относительно высокой плотности характеризуется ясно очерченной границей между столбом дуги и окружающей средой, высокой плотностью тока в столбе дуги (десятки-сотни ампер на миллиметр), высокой температурой газа внутри столба дуги (5000-25000 К), высокой плотностью тока на катоде и малым напряжением у катода (10-20 В).
Дуга приводит к значительному износу аппарата, но, с другой стороны, играет положительную роль. При отключении постоянного тока значительная часть электромагнитной энергии, запасенной в цепи, преобразуется в тепловую энергию дуги, которая отводится в окружающую среду. Это ведет к снижению перенапряжений, опасных для изоляции оборудования. При переменном токе процесс гашения дуги проходит вблизи нулевой паузы тока, когда электромагнитная энергия цепи близка к нулю. В результате этого вероятность появления опасных перенапряжений резко уменьшается.
Дата: 2019-02-25, просмотров: 862.