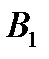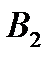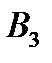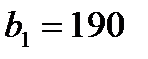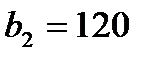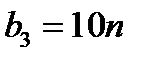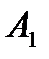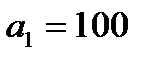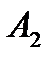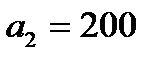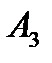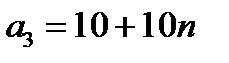Задание 1. Задача оптимального производства продукции.

Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В и С. Потребность 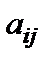 на каждую единицу 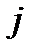-го вида продукции 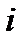-го вида сырья, запас  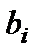соответствующего вида сырья и прибыль 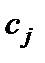, от реализации единицы  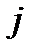-го вида продукции заданы таблицей:

Виды	Виды продукции		Запасы
сырья	I	II	сырья
А		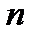2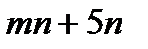
В	1	1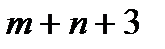
С	2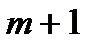
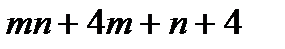
Прибыль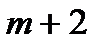
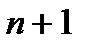
План (ед.)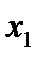

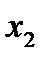
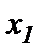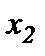1.1 Для производства двух видов продукции I и II с планом  и  единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее  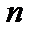единиц обоих видов продукции.

1.2 Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим (графическим) методом. Определить соответствующую прибыль .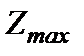

1.3 В условиях задачи симплекс - методом найти оптимальный план 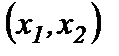производства продукции, обеспечивающий максимальную прибыль 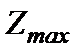. Определить остатки каждого вида сырья.

Задание 2. Транспортная задача.

На трех складах 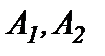 и 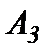 хранится 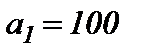, 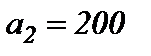и 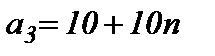единиц одного и того же груза. Этот груз требуется доставить трем потребителям 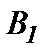, 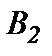и 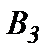, заказы которых составляют 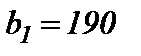,  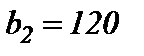и 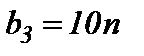единиц груза соответственно.

Стоимости перевозок 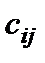 единицы груза с  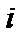- го склада  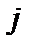- му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:

Потребности Запасы
			4		2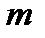
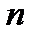
					5		3
			1		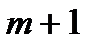		6

2.1. Сравнивая суммарный запас 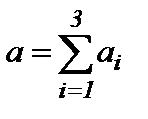 и суммарную потребность  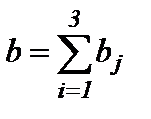в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой.

2.2. Составить первоначальный план перевозок. (Рекомендуется воспользоваться методом наименьшей стоимости или северо-западного угла).

2.3. Проверить, является ли первоначальный план оптимальным в смысле суммарной стоимости перевозок, и если это не так, то провести оптимизационные итерации и получить оптимальный план, обеспечивающий минимальную стоимость перевозок .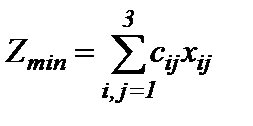

Найти эту стоимость. (Рекомендуется пользоваться методом потенциалов).

Раздел 3. Принятие решений в условиях неопределённости и риска

Задание 1. Принятия решений с помощью дерева решений

Предприятие покупает программный продукт и ему предлагают оплатить обслуживание в течение срока эксплуатации (3 года) в размере 800 рублей, известно, что сбои в работе программы происходят не более 3 раз за срок эксплуатации, отладка работы программного продукта за один вызов оценивается в 80 рублей, если имеется оплаченное обслуживание, и в 450, если нет. Вероятность того, что сбоев не будет равна 0,4, что сбой будет 1 раз – 0,35, 2 раза – 0,15. Определить вероятность того, что будет 3 сбоя, построить дерево решений и определить, как должен поступить пессимист, оптимист и рациональный человек.

Задание 2. Выполнить следующее задание, пройдя все этапы метода анализа иерархий и выбрав наилучший вариант:

Определить город (или район в Вашем городе), наилучшим образом приспособленный к проживанию (у каждого человека могут быть свои предпочтения). Для решения задачи создать полную трёхуровневую иерархию, содержащую не менее трёх критериев, по которым идёт оценка (например, качество инфраструктуры, экология и т.д.), и не менее трёх вариантов для выбора.

Задание 3. Составить игровую матрицу для первого задания и определить оптимальную стратегию поведения, воспользовавшись различными подходами.