Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

       Если тонкая и высокая балка прямоугольного сечения изгибается в главной плоскости с наибольшей жесткостью, то плоская форма изгиба за критическим

и нагрузками становится неустойчивой и происходит выпучивание балки.

       Рассмотрим тонкую высокую балку, загруженную посредине пролета силой Р

 

а)                                                                            в)    y       y₁

         Z                                                                      U

                               P

 

                                                                   Z h     M_1(X)                

                                                                                                       M_X  V

                                                                                            d     b

                   l/2               l/2                                                               x₁

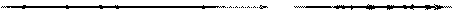                                                                                           b

 

 

б)

 

 

                                 P

 

       В самый начальный момент потери устойчивости некоторое сечение на расстоянии Z от левой опоры повернулось на малый угол b, т.е. его новая ось у₁ наклонена к вертикали под этим углом. Горизонтальное смещение средней линии сечения = U, вертикальное = V.

       Т.е. в момент потери устойчивости, наряду с вертикальным изгибом, появляется изгиб балки в боковом направлении, а также ее кручение.

       Определим дополнительную потенциальную энергию накапливаемую полосой в момент потери устойчивости, учитывая боковой изгиб и кручение полосы.

       Момент, изгибающий полосу в боковом направлении

                        

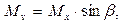
учитывая, что угол b бесконечно мал sin b = b

                              

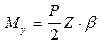
       Потенциальная энергия, накапливаемая в результате бокового изгиба

       ,

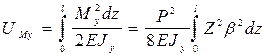где J_у - момент инерции сечения относительно оси У.

 

       Учитывая, что сила приложена посредине длины балки, возьмем интеграл на половине ее длины и результат удвоим

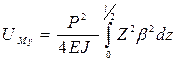                   (1)

       Определим потенциальную энергию, накапливаемую в полосе за счет ее кручения

,

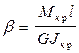или

,

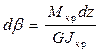отсюда

.

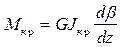Потенциальная энергия в элементе бесконечно малой длины

,

 

.

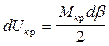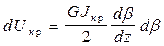Умножим это выражение и разделим на dz

.

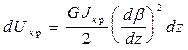Потенциальная энергия в полосе кручения

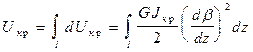
или

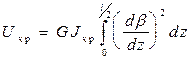                                                         (2)

 

       Полная потенциальная энергия внутренних сил, накапливаемая полосой после потери устойчивости

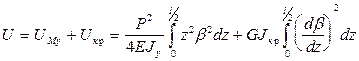           (3)

 

 

Определим работу внешних сил в момент потери устойчивости полосой

        P

                                                                   Ввиду малости перемещений, работа внешних

                    P    d                           сил при повороте сечения = 0

 

Работа Р на перемещении d равна

А = Р×d ,

без коэффициента 1/2 т.к. в момент потери устойчивости сила имеет свою постоянную величину.

       Перемещение d определим оп интегралу Мора:

 

 ,

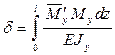где М_у - момент, вызывающий боковой изгиб силой Р :      ;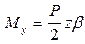

- то же единичной силой :      .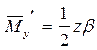

 

Тогда:

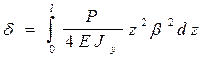
или:

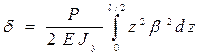           (4)

 

       Приравнивая потенциальную энергию внутренних сил работе внешних сил:

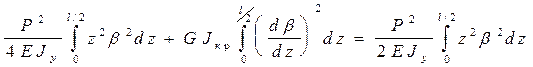
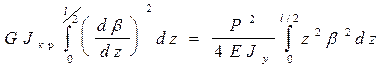
или

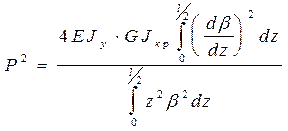                (5)

 

       Задаемся выражением для углов закручивания сечений, удовлетворяющих граничным условиям задачи:

        ,                 ;

 

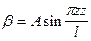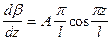1) при z = 0                                   b = 0

       2) при z = l                                    b = 0

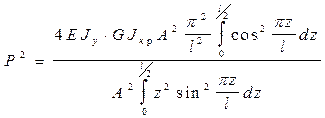
       Вычислив интегралы:

 

                                                   (6)

 

 

       Точное решение

 

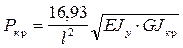
       Для двутаврового сечения:

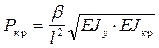                                              (7)

 

где b - коэффициент, определяемый по таблицам справочников.