Матрица жесткости КЭ в местной системе осей координат [r]j’ устанавливает связь между единичными перемещениями и усилиями в узловых точках, для горизонтально расположенного элемента.
Как уже отмечалось, основная система МКЭ представляет собой совокупность отдельных стержней, которые соединяются между собой жестко или с помощью шарнира.
Следовательно, все многообразие КЭ можно свести к трем типам элементов:
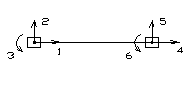 |
а) элемент с двух сторон ограниченный жесткими узлами, такой элемент имеет шесть степеней свободы, т.е. неизвестными являются шесть возможных перемещений узловых точек элемента
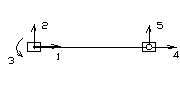 |
б) элемент с одной стороны ограниченный жестким узлом, а с другой шарнирным, такой элемент имеет пять степеней свободы
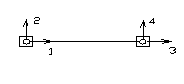 |
г) элемент с двух сторон ограниченный шарнирными узлами, такой элемент имеет четыре степени свободы
Рассмотрим формирование матриц жесткости для показанных выше трех типов КЭ, в местной системе осей координат.
Для элемента с шестью степенями свободы (тип а) матрица жесткости будет иметь вид
[r]j’= 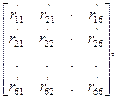
где r12’ - реактивное усилие в связи 1 от единичного перемещения связи 2 и т.д.
В блочном виде матрица [r]jэ будет иметь вид
[r]j’= 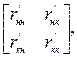

где rнк’ - блок реакций в связях, наложенных на начальный узел, от единичных перемещений связей, наложенных на конечный узел КЭ и т.д.
Численные значения реакций будем определять используя таблицы метода перемещений. Знак реакций будет положительным, если направление реакций совпадает с положительным направлением перемещений Vj.
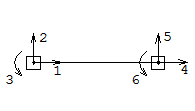 |
1.Формирование матрицы жесткости для элемента с шестью степенями свободы (тип а)
Зададим последовательно единичные перемещения связям V1=1, V2=1...V6=1.
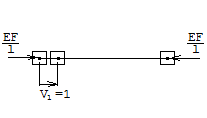 |
1) V1=1
В соответствие с законом Гука
Dl = 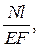
 Dl = V1 = 1, N =
Dl = V1 = 1, N = 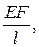
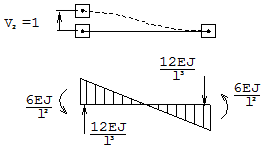 |
2) V2=1
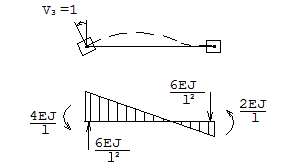 |
3) V3=1
и т.д. задаем V4 = 1, V5 = 1, V6 = 1
Расставляя реакции в соответствующие ячейки, получим матрицу жесткости для элемента с шестью степенями свободы
[r]j’ = 
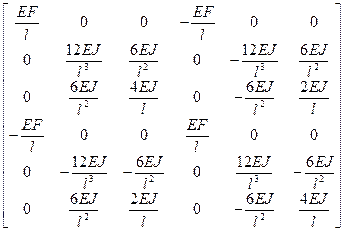


Запишем матрицы жесткости для двух других типов элементов, формируя их аналогично предыдущей.
2. Матрица жесткости для элемента с пятью степенями свободы (тип б) будет иметь вид
[r]j’ = 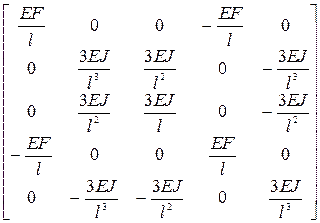

3. Матрица жесткости для элемента с четырьмя степенями свободы (тип в) запишется
[r]j’ = 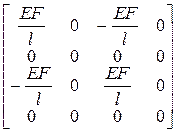
Лекция 3. Матрица преобразований (направляющих косинусов)
Рассмотрим теперь КЭ в составе рамы, расположенный под углом  a к оси Х в общей системе осей координат.
a к оси Х в общей системе осей координат.
Необходимо перейти от матрицы реакций [r]’j в местной системе осей координат к матрице [r] в общей системе координат.
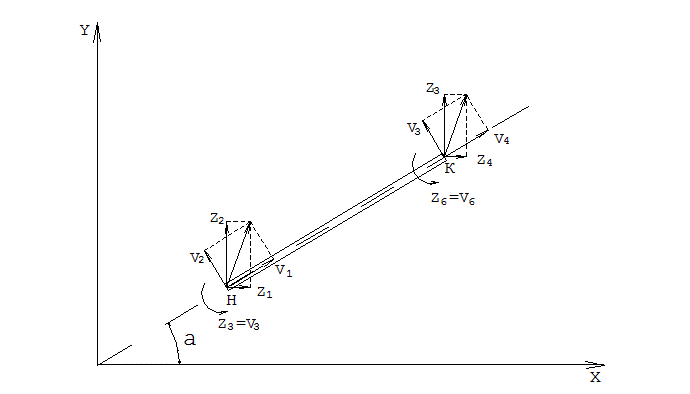
Задачу решаем следующим образом. В начале построим матрицу [c]j, которая преобразует перемещения КЭ {z}j в общей системе осей координат в перемещения {v}j, по выражению
{v}j = [c]j {z}j
V1 = Z1 cosa + Z2 sina
V2 = -Z1 sina + Z2 cosa
V3 = Z3
V6 = Z6
V4 = Z4 cosa + Z5 sina
V5 = -Z4 sina + Z5 cosa
В матричной форме приведенная выше запись будет иметь вид


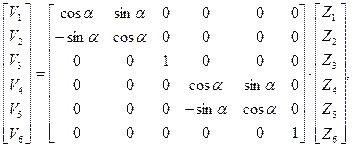

или в блочной форме
[c]j = 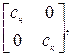
где для жесткого узла
[c]н,к = 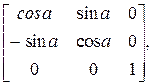
для шарнирного узла
[c]н,к = 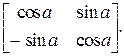
Так как мы рассматриваем плоские упругие системы, то векторы узловых усилий и узловых перемещений, как для отдельного элемента, так и для сооружения в целом, связаны между собой линейно
{S}j’ = [r]j’{V}j - в местной системе осей координат.
{S}j = [r]j {Z}j - в общей системе осей координат
Кроме того
{V}j = [c]j{Z}j,
Аналогично
{S}j’ = [c]j{S}j,
где {S}’,{S}-узловые усилия КЭ соответственно, в местной и общей системах осей координат.
Тогда
{S}j = [c]j-1 {S}j’ = [c]j-1[r]j’{V}j = [c]j-1[r]j’[c]j{Z}j.
Для матрицы направляющих косинусов выполняется равенство
[c]j-1 = [c]jT,
Тогда
{S}j = [c]jT [r]j’ [c]j{Z}.
Обозначим
[r]j = [c]jT [r]j’ [c]j - это выражение и является формулой для вычисления матрицы жесткости КЭ в общей системе осей координат.
При формировании матриц жесткости отдельных элементов [r]j’ должны быть зафиксированы начало и конец каждого стержня, так как от этого зависит знак угла a, определяющего ориентацию стержня в общей системе осей координат ХОY.
Дата: 2019-02-19, просмотров: 335.