Рассмотрим раму, нагруженную силами, приложенными в узлах.


 Р Р
Р Р
 |

 Пренебрегая изменением длин стержней и их весом, можно считать, что при достаточно малых значениях сил все стержни остаются прямыми и в них возникают только продольные усилия. При достижении нагрузкой критического значения наряду с исходным появляется смежное, деформированное состояние равновесия.
Пренебрегая изменением длин стержней и их весом, можно считать, что при достаточно малых значениях сил все стержни остаются прямыми и в них возникают только продольные усилия. При достижении нагрузкой критического значения наряду с исходным появляется смежное, деформированное состояние равновесия.
Такой подход является идеализированным (как и при расчете центрально сжатых стержней), т.к реальные нагрузки имеют эксцентриситет приложения, а также имеется начальный прогиб элементов от их собственной массы.
Для расчета рам на устойчивость можно использовать те же методы, что и для расчета на прочность: метод сил, метод перемещений, смешанный метод и т.др.
Смысл расчета рам на устойчивость заключается в определении для всех сжатых элементов критических сил Ркр и их расчетных длин 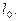
Расчету на устойчивость предшествует расчет рамы на прочность любым из известных методов. Затем рама рассчитывается на устойчивость под действием только узловых сжимающих нагрузок, которые берут из эпюры N расчета на прочность.
Порядок расчета рам на устойчивость методом перемещений
Порядок расчета рам на устойчивость аналогичен расчету на прочность.
1. Определяют степень кинематической неопределимости рамы
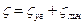 ,
,
где  степень угловой подвижности рамы, равна числу жестких узлов;
степень угловой подвижности рамы, равна числу жестких узлов; 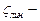 степень линейной подвижности, равна числу возможных независимых перемещений узлов рамы.
степень линейной подвижности, равна числу возможных независимых перемещений узлов рамы.
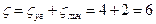

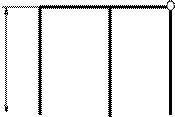
2. Выбирают основную систему метода перемещения, для чего в каждый жесткий узел вводят упругоподатливые защемления (связи 1го рода), а по направлению возможных перемещений - дополнительные опорные стерженьки (связи 2го рода).
Например:

 P1 P2 P1 P2
P1 P2 P1 P2
 | |||
 | |||
1 2 3
h
 |  | ||||||||||||
 |  | ||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 l1 l2
l1 l2
 |
Заданная система Основная система
3. Составляют систему канонических уравнений. В отличие от аналогичных уравнений расчета на прочность (поперечный изгиб) грузовые коэффициенты Rip равны нулю, т.к. узловые нагрузки не вызывают реактивных усилий в дополнительных связях. Система канонических уравнений записывается :
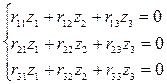
Действие внешней нагрузки в данном случае учитывается при вычислении единичных коэффициентов rik = rki , т.к. при единичных смещениях дополнительных связей деформируемые элементы, в пределах которых действуют сжимающие усилия, находятся в условиях продольно-поперечного изгиба.
4. Порядок определения опорных реакций с учетом сжимающих сил покажем на примере балки, у которой один конец жестко защемлен, другой шарнирно оперт.



 MA jA=1 N
MA jA=1 N 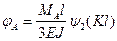





 N
N

 A RA B
A RA B
i RB где


N N




 MA
MA
 |  | ||
RA RB Для того, чтобы основная система и


 заданная были равноценны необходимо чтобы МА имел такую
заданная были равноценны необходимо чтобы МА имел такую 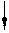 величину, при которой jА=1.
величину, при которой jА=1.

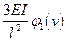


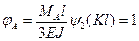 ,
,
отсюда
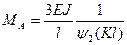 .
.
 Обозначим:
Обозначим:
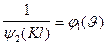 , где
, где 
т.е. 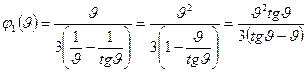
 |
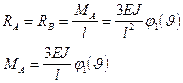
Аналогично получают реакции опор и в других случаях.
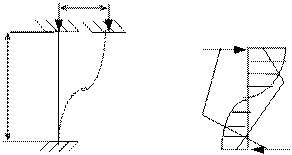
| Схемы и эпюры | Коэффициенты |
 Z=1 P
Z=1 P
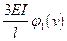 i EI
i EI
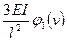
|
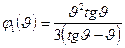
|
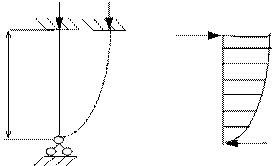 P P P P 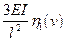 l
l 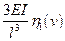
|
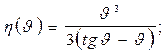
|
 P
Z=1
P
Z=1 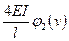 l
l
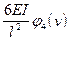
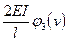
|
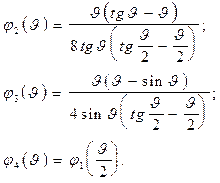
|
 Z=1
P P
l
Z=1
P P
l 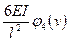 
|
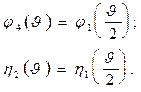
|
Z=1
P
 l
l 
|
5. Строят эпюры от единичных смещений наложенных связей. В пределах элементов, которые сжаты внешней нагрузкой, эпюры криволинейны и строятся в соответствии с приведенной выше таблицей. В пределах элементов не подверженных сжатию, эпюры прямолинейны и строятся по таблицам обычного метода перемещений (как при расчете на прочность) .
 P1 P2 P1 P2
P1 P2 P1 P2
 1 2 3
1 2 3

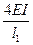
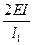
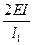
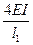
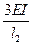


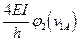
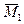

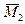
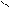 A B C
A B C
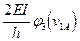
Z3=1
P1 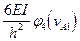 P2
P2 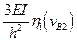
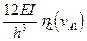
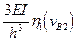
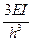

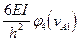
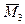
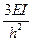
6. Коэффициенты системы канонических уравнений определяют как и в обычном методе перемещений.
r11
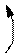




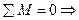
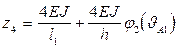
 |
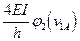
и т.д.
 | |||||
 |  | ||||




 r33
r33
 | |||||
 |  | ||||

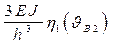
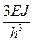
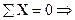
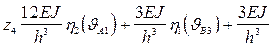
7. Для заданной системы уравнений (без свободных членов), возможны два решения: первое, когда все zi = 0, такое решение нас не устраивает, т.е не соответствует условиям задачи; и второе решение, когда детерминант системы, составленный из единичных коэффициентов = 0.

Раскрывая этот определитель, получаем сложное трансцендентное уравнение, для решения которого необходимо вначале выразить все параметры vi через один. Затем уравнение решается:
1) методом подстановки;
2) графическим методом.
Метод подстановки самый примитивный способ решения. Применяется для простейших характеристических уравнений.
Сущность графического способа заключается в следующем:
- выбираем произвольное значение параметра vi и находим det1 = f (v)
v1 => det1
v2 => det2
v3 => det3
и т.д.
На основании полученных значений строим график функции det = f (v).
det
 det = f (v)
det = f (v)
v1 v2 v3 v4 v5 v
vкр
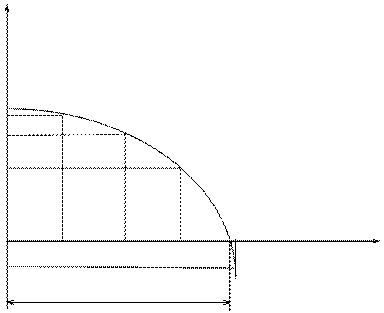
Наименьшее значение параметра v, при котором det = 0 называется vкр.
8. Для стойки, параметры которой мы принимаем за исходные определяем критическую силу:

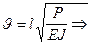
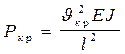
и расчетную длину стержня:

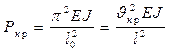 , отсюда
, отсюда
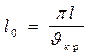 где: l0 - расчетная длина стержня;
где: l0 - расчетная длина стержня;
l - геометрическая длина стержня
или коэффициент приведения геометрической длины к расчетной:
 |
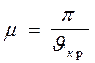
9. Зная соотношение между параметрами остальных элементов и исходным элементом, определяют vкр для всех остальных сжатых стержней.
10. Затем для всех сжатых стержней определяют Ркр и l0..
Дата: 2019-02-19, просмотров: 362.