1. Вывод дифференциального уравнения кругового бруса
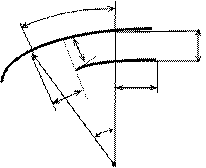dS dS - длина элемента mn до деформации,
n R - радиус кривизны
m W+dW m1n2 положение элемента mn после
W деформации.
V+dV
V
R dQ
O
Обозначим проекции перемещения точек m и n через: V - проекцию перемещения на касательную и W - проекцию перемещения на радиус.
Определим относительную деформацию элемента dS. Для этого воспользуемся принципом наложения и будем определять отдельно деформацию элемента от перемещений W и V.
1) W = 0
V+dV
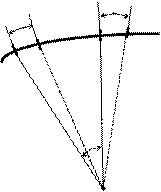V
m m1 n n1
dQ
O
Абсолютная деформация элемента dS равна dV, а относительная деформация
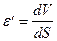(1)
2) V = 0. Бесконечно малой величиной dW пренебрегаем
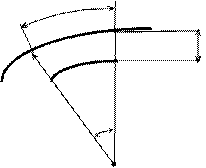dS до деформации
n dS = Rdq
m W после деформации
n1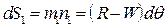 
m1
R dQ
O
Абсолютная деформация элемента dS
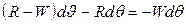
Относительная деформация:
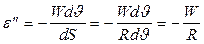, (2)
т.к. dS = RdJ.
Полная относительная деформация элемента:
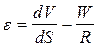(3)
Кривизна элемента до деформации
dS = Rdq Þ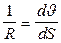 
Определим изменение элемента за счет его деформации. Углы поворота касательных, проведенных к точке m:
1) W = 0
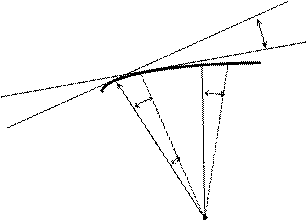a
m m1 n n1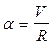 
V V+dV
R
 |
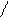a
O
2) V = 0
в этом случае пренебречь
величиной dW нельзя
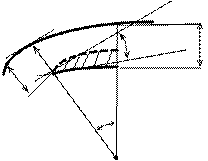n
m
W b W+dW
m1 n1 Заштрихованный треугольник ввиду
малых величин можно считать
прямолинейным, тогда:
R
O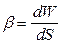 
Суммарный угол поворота касательной
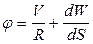(4)
Изменения кривизны деформированного элемента:
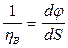
Продифференцируем выражение (4):
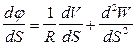(5)
Пренебрегая удлинением элемента dS, т.е. e = 0, из уравнения (3) имеем:
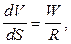
подставляя это значение в (5) и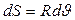 
.
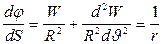(6)
Из сопротивления материалов известно дифференциальное уравнение изогнутой оси бруса:
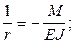(7)
подставив (7) в (6) получим дифференциальное уравнение кривого бруса:
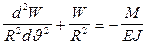
или
 |
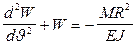(8)
2. Устойчивость кругового кольца при радиальной нагрузке
 |
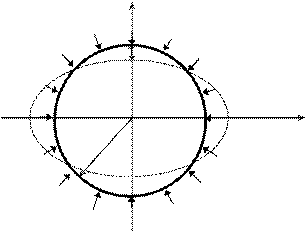y q - интенсивность равномерно
K распределенной радиальной
нагрузки.
W K1
q
x
R
При q < qкр кольцо сохраняет первоначальную форму равновесия и в нем возникают только продольные усилия сжатия.
При q ³ qкр кольцо теряет устойчивую форму равновесия, приобретая овальную форму и в нем, наряду с продольными усилиями появляются изгибающие моменты.
Рассмотрим элемент dS до потери устойчивости:
y
q dS
N N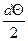 
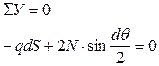
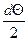ввиду малости угла q
dQ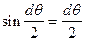 
О
тогда
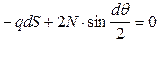, dS = Rdq
;
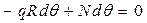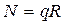(а)
После потери устойчивости точка К переместится в точку К1, прогиб стенки кольца составляет W. В деформированном состоянии продольная сила вызывает в кольце изгибающий момент:
Подставим это значение момента в дифференциальное уравнение бруса (8):
,
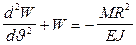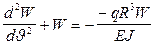
или
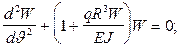(б)
Обозначим
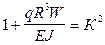(с)
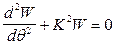(d)
Решение этого однородного дифференциального уравнения запишется:
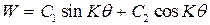(е)
Значение коэффициентов С1 и С2 найдем из граничных условий:
учитывая, что на осях симметрии W’=0
1) при q= 0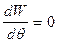 
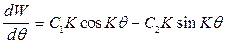
0 = С1К; С1 = 0
2) при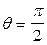 
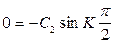
С2 = 0; К = 0
Следовательно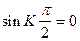 
, а это возможно при :
1) К = 0 - противоречит условию задачи (см. выше)
2) К=2, sin p = 0.
Из выражения (с) получаем
,
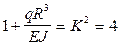отсюда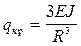 
(f)
3. Устойчивость двухшарнирной круговой арки
Рассмотрим круговую арку загруженную равномерно распределенной радиальной нагрузкой q.
q
A B
Q
a R
O
Дифференциальное уравнение кривого бруса по аналогии с кольцом
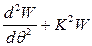, где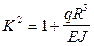 
Решение его:
,
где q - угол изменяющийся от 0 до a.
Граничные условия задачи:
1) при q = 0 W = 0;
0 = С2
2) при q = a W = 0;
0 = C1 sin Ka; C1 ¹ 0
Следовательно sin Ka =0
; 
; 
;
; 
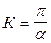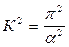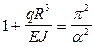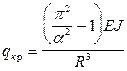
Дата: 2019-02-19, просмотров: 203.
