Учет погрешностей квадратурных формул методом двойного пересчета (методом Рунге).

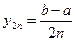Выбираем некоторое натуральное число n и проводим вычисления по одной из квадратурных формул дважды: при разбиении отрезка на n и на 2n частей (с шагом  и  соответственно). Обозначим полученные результаты через I_n и I_{2 n}. Лучшим приближением будет I_{2 n}, которое и считаем приближенным значением интеграла. Приближенные оценки погрешности числа I_{2 n} в случае квадратурных формул следующие:

для формул прямоугольников с левыми и правыми ординатами ;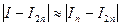

для формулы прямоугольников с центральными ординатами и для формулы трапеций

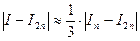; для формулы Симпсона .

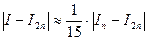Пример. Вычислить значение определенного интеграла 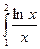, используя квадратурные формулы. Оценить погрешность методом двойного пересчета ( ).

Решение. Составим таблицы значений подынтегральной функции пр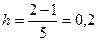и  и .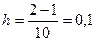

	1	1,2	1,4	1,6	1,8	2
	0	0,152	0,240	0,294	0,327	0,347

	1	1,1	1,2	1,3	1,4	1,5	1,6	1,9	1,8	1,9	2
	0	0,087	0,152	0,202	0,240	0,270	0,294	0,312	0,327	0,338	0,347

Воспользуемся квадратурными формулами:

1. Формула прямоугольников с левыми ординатами: ;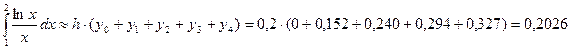

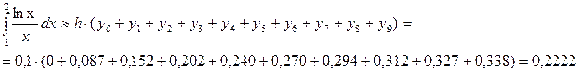
2.   Формула прямоугольников с правыми ординатами:

;

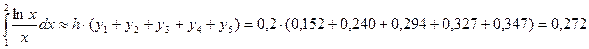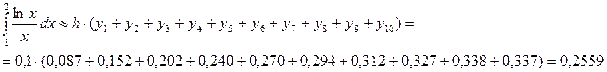
3.  Формула трапеций:

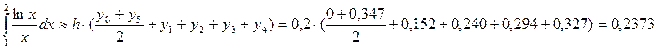
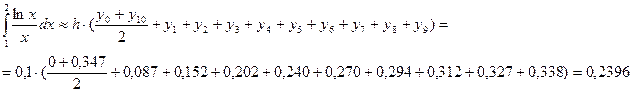
4. Формула Симпсона:

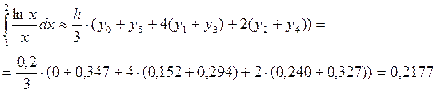
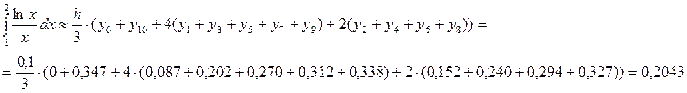5. Формула прямоугольников с центральными ординатами: .

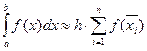Составим таблицы значений данной функции для середин отрезков:

	1,1	1,3	1,5	1,7	1,9
	0,087	0,202	0,270	0,312	0,338

	1,05	1,15	1,25	1,35	1,45	1,55	1,65	1,75	1,85	1,95
	0,046	0,122	0,179	0,222	0,256	0,283	0,304	0,320	0,333	0,342

;

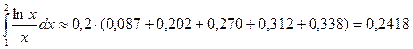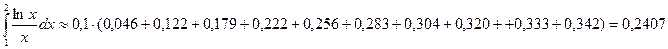
Оценим погрешности каждой формулы:

1. Для формулы прямоугольников с левыми ординатами: ;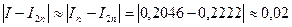

2. Для формулы прямоугольников с правыми ординатами: ;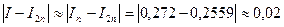

3. Для формулы трапеций ;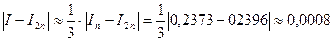

4. Для формулы Симпсона ;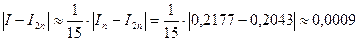

5.Для формулы прямоугольников с центральными ординатами .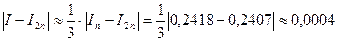

Задание

Вариант 1

Вычислить интеграл 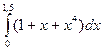 по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 3. Оценить погрешность приближения методом двойного пересчета.

Вариант 2

Вычислить интеграл 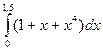 по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 6. Оценить погрешность приближения методом двойного пересчета.

Вариант 3

Вычислить интеграл 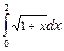 по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 4 . Оценить погрешность приближения методом двойного пересчета.

Вариант 4

 Вычислить интеграл 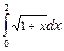 по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 8. Оценить погрешность приближения методом двойного пересчета.

Вариант 5

Вычислить по формулам прямоугольников, формуле трапеций и формуле Симпсона приближенное значение определенного интеграла 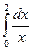 при n = 10 с тремя десятичными знаками.

Вариант 6

Вычислить по формулам прямоугольников, формуле трапеций и формуле Симпсона приближенное значение определенного интеграла 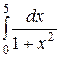 при n = 5 с тремя десятичными знаками.

Содержание отчёта

 Отчёт о проделанной работе должен содержать:

- название темы практического занятия;

- цели практического занятия;

- условие задачи;

- подробное решение задачи;

- ответ.

Контрольные вопросы

1. Как найти узлы квадратуры?

2. На чем основываются численные методы вычисления определенного интеграла?

3. Как можно получить формулы прямоугольников с левыми, правыми и центральными ординатами?

4. Как можно получить формулу трапеций?

5. Чем отличается формула Симпсона от формулы трапеций?

6. Какая из формул дает лучший результат?

7. В чем суть метода двойного пересчета?

Литература:

   1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов

Н/Д: Феникс 2014. – 380с.

     2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.

     3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,

         2000 – 560с.

   4. Методическая копилка учителя математики www.metod-kopilka.ru