Ряд, членами которого являются функции от х, называют функциональным рядом:

.

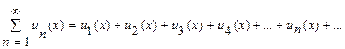Совокупность числовых значений аргумента 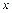, при которых функциональный ряд сходится, называют его областью сходимости.

Среди функциональных рядов в математике и ее приложениях особую роль играют ряды, членами которых являются степенные функции аргумента 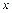. Такие ряды называют степенными рядами:

.

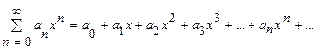Числа 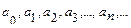 называют коэффициентами ряда.

Об области сходимости степенного ряда можно судить, исходя из теоремы Абеля:

 Если степенной ряд сходится при 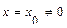, то он абсолютно сходится при всех значениях 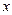, удовлетворяющих неравенству 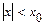. Если ряд расходится при 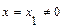, то он расходится и при всех 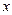, удовлетворяющих неравенству .

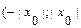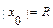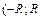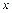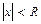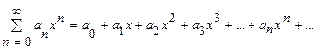Интервал ) называют интервалом сходимости степенного ряда. Положив , интервал сходимости можно записать в виде ). Число R называют радиусом сходимости степенного ряда, т. е. это такое число, что при всех , для которых , ряд  абсолютно сходится, а при  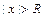ряд расходится.

Когда степенной ряд сходится только в одной точке 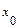, то 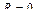. Если же степенной ряд сходится при всех значениях  (т. е. во всех точках числовой оси), то .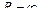

Радиус сходимости степенного ряда находить так: .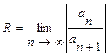

Найти интервал сходимости степенного ряда.

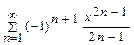. Решение. Найдем радиус сходимости: , ,

.

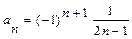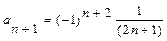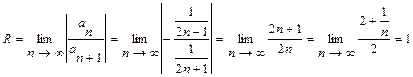Значит, ряд абсолютно сходится на интервале .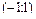

Задание

Вариант 1

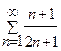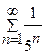Задача 1. Определите сходимость ряда: а) ; б) ; в) .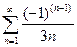

Задача 2. Найдите радиус и интервал сходимости ряда .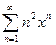

Вариант 2

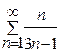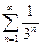Задача 1. Определите сходимость ряда: а) ; б) ; в) .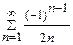

Задача 2. Найдите радиус и интервал сходимости ряда .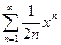

Вариант 3

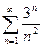Задача 1. Определите сходимость ряда: а) ; б) ; в) .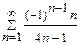

Задача 2. Найдите радиус и интервал сходимости ряда .

Вариант 4

Задача 1. Определите сходимость ряда: а) 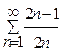; б) ; в) .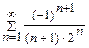

Задача 2. Найдите радиус и интервал сходимости ряда .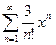

Вариант 5

Задача 1. Определите сходимость ряда: а) 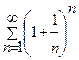; б) ; в) .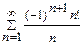

Задача 2. Найдите радиус и интервал сходимости ряда .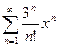

Вариант 6

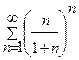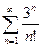Задача 1. Определите сходимость ряда: а) ; б) ; в) .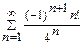

Задача 2. Найдите радиус и интервал сходимости ряда .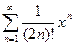

Содержание отчёта

 Отчёт о проделанной работе должен содержать:

- название темы практического занятия;

- цели практического занятия;

- условие задачи;

- подробное решение задачи;

- ответ.

Контрольные вопросы

Контрольные вопросы.

1. В чем разница между сходящимся рядом и расходящимся?

2. Как применяют  необходимый признак сходимости числовых рядов?

3. Как применяют признак Даламбера?

4. Как применяют признак Лейбница?

5. Какой ряд называется условно сходящимся?

6. Как найти радиус сходимости степенного ряда?

7. Какова связь между радиусом сходимости степенного ряда и его интервалом сходимости?

Литература:

1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов

Н/Д: Феникс 2014. – 380с.

     2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.

     3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,

         2000 – 560с.

    4. Методическая копилка учителя математики www.metod-kopilka.ru

Практическое занятие № 15