Цель: в результате выполнения практической работы, обучающиеся должны уметь вычислять пределы функций, раскрывая неопределенности , , 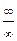 и используя замечательные пределы.

Пояснения к работе

Пусть функция определена в некоторой окрестности точки 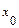, кроме, быть может, самой точки . Число А называется пределом функции ƒ(x) при 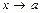, если для любого сколь угодно малого ε > 0 найдется такое δ > 0, что при 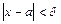. Запись .

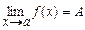Если предел функции 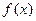в точке  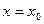существует, то он единственный.

Аналогично, 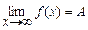, если  при .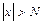

Функцию 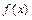 называют бесконечно большой при 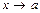, если .

Функцию называют бесконечно малой при 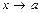, если .

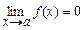Если функция ƒ(x) – бесконечно малая, то функция 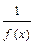есть бесконечно большая функция и наоборот: если функция ƒ(x) – бесконечно большая, то  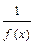- бесконечно малая.

Теоремы о пределах.

Теорема 1. Пусть существуют, тогда ;

; .

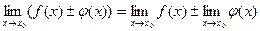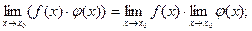
Теорема 2. Предел многочлена 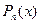 в точке  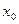равен значению этого многочлена в точке 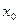, т. е. .

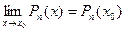Вычислить пределы:

1. .

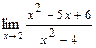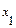2. . Здесь пределы числителя и знаменателя равны 0, т. е. мы получили неопределенность . Разложим на множители числитель и знаменатель дроби. Числитель разложим на множители по формуле , где  и 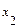 корни уравнения 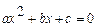. Знаменатель разложим на множители по формуле . .              

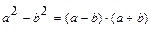3. 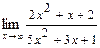. При  числитель и знаменатель дроби – бесконечно большие функции, т. е. дана неопределенность 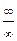. Раскрывают такую неопределенность делением числителя и знаменателя дроби на наибольшую степень переменной знаменателя, в данном случае на . .

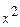Замечательные пределы позволяют раскрыть неопределенности  и .

Первый замечательный предел: 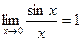 или .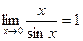

Второй замечательный предел: 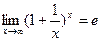 или .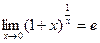

Вычислить пределы функций:

1. .

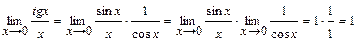2. 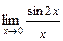. Решение. Обозначим 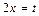, тогда 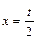. Если 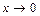, то 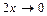, а значит .

.

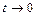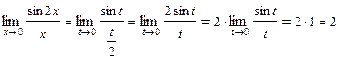3. 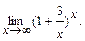 Решение. Сделаем замену переменной, полагая 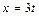, тогда при  и 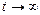. Следовательно, .

4. 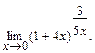  Решение. Обозначим 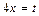, тогда 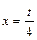. Если 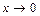, то 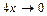, а значит .

.

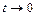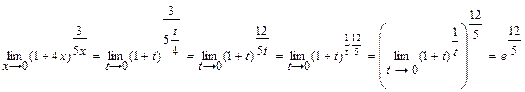Здесь использовали свойство предела. «Пусть дана функция ƒ(φ(х)), причем функция ƒ - непрерывная на множестве значений функции  у = φ(х), тогда ».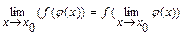

Задание.

Вариант 1.

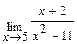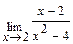Задача 1. Найдите пределы функций: а) ; б) ;  в) .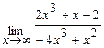

 Задача 2. Примените замечательные пределы для нахождения пределов функций: а) ;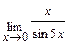

б) .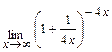

Вариант 2.

Задача 1. Найдите пределы функций: а) 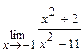; б) ;  в) .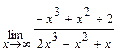

Задача 2. Примените замечательные пределы для нахождения пределов функций: а) ;                                       б) .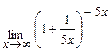

Вариант 3.

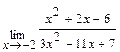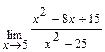Задача 1. Найдите пределы функций: а) ; б) ;  в) .

Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 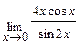;                                б) .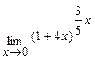

Вариант 4.

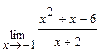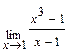Задача 1. Найдите пределы функций: а) ; б) ;  в) .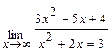

Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 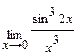;                                   б) .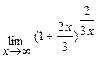

Вариант 5.

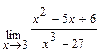Задача 1. Найдите пределы функций: а) ; б) ;  в) .

Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 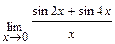;                        б ) .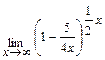

Вариант 6.

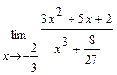Задача 1. Найдите пределы функций: а) ; б) ;  в) .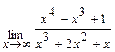

Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 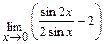; б) .

Содержание отчёта

 Отчёт о проделанной работе должен содержать:

- название темы практического занятия;

- цели практического занятия;

- условие задачи;

- подробное решение задачи;

- ответ.

Контрольные вопросы

1.    Какая существует связь между бесконечно большой и бесконечно малой функциями?

2.    Как раскрывают неопределенности ?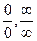

3.    Какими теоремами о пределах вы пользовались при вычислении пределов?

4.    Какие неопределенности помогают раскрыть замечательные пределы?

Литература:

1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов

Н/Д: Феникс 2014. – 380с.

     2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.

     3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,

         2000 – 560с.

    4. Методическая копилка учителя математики www.metod-kopilka.ru

Практическое занятие № 8