Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называют промежутками выпуклости графика функции.

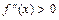Выпуклость вверх или вниз кривой, являющейся графиком функции , характеризуется знаком ее второй производной: если в некотором промежутке , то кривая выпукла вниз на этом промежутке, если же 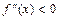, то кривая выпукла вверх на этом промежутке.

Точку графика функции , разделяющую промежутки выпуклости противоположных направлений, называют точкой перегиба. Если при переходе через критическую точку вторая производная меняет знак, то график функции имеет точку перегиба.

Правило нахождения промежутков выпуклости и точек перегиба графика функции .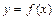

1. Найти вторую производную .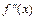

2. Найти критические точки функции 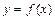 по второй производной, т. е. точки в которых вторая производная 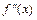обращается в нуль или не существует (терпит разрыв).

3. Определить знак второй производной 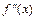 в каждом промежутке, на которые найденные критические точки делят область определения функции . При этом, если на промежутке 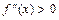 ( ), то на этом промежутке график функции направлен выпуклостью вниз (вверх). Точка 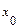является точкой перегиба графика функции, если она разделяет промежутки выпуклости противоположных направлений.

4. Вычислить значение функции в точках перегиба.

Пример. Найти точки перегиба кривой и промежутки выпуклости графика функции .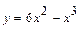

Решение. Область определения этой функции – все множество действительных чисел, т. к. функция задана многочленом. Найдем вторую производную данной функции , .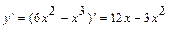

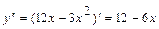Найдем критические точки по второй производной. Втора производная определена на всем множестве действительных чисел. Найдем нули второй производной. , .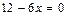

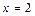Определим знак второй производной на каждом промежутке, результаты внесем в таблицу.

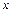
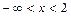
		2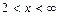
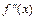
	+	0	–
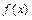
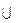	График функции выпуклый вниз	16 Точка перегиба	График функции выпуклый вверх

Пример. Построить график функции: ;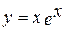

D(y)=R

Функция не является четной и нечетной, не периодична.

у = 0 при х = 0. Два промежутка знакопостоянства (-∞;0) и (+∞;0). Для  x 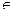(-∞;0) y<0, для x 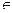(+∞;0) y>0. Рассмотрим поведение функции на концах промежутков: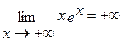    

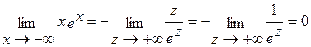 (по правилу Лопиталя).

Найдем производную данной функции:

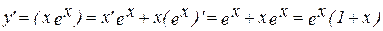
y′=0 при х = - 1, эта точка делит область определения функции на два промежутка (-∞;-1) и (-1;+∞)

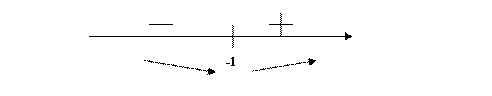
Исследуемая функция в промежутке xЄ(-∞;-1) убывает, а для xЄ(-1;+∞) - возрастает точка х = - 1 – точка минимума .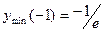

Найдем вторую производную функции:

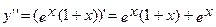
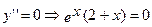 при х=-2

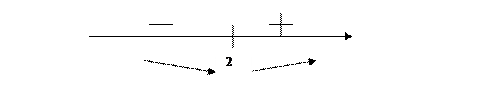
для 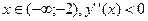, следовательно, график функции на этом интервале выпуклый вверх.

Для  следовательно, график функции на данном интервале выпуклый вниз.

По полученным данным строим график функции:

Задание

Вариант 1

Задача. Исследовать функцию  на монотонность и экстремумы, построить график.

Вариант 2

Задача. Исследовать функцию 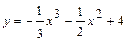 на монотонность и экстремумы,  построить график.

Вариант 3

Задача. Исследовать функцию 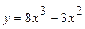 на монотонность и экстремумы, построить график.

Вариант 4

Задача. Исследовать функцию 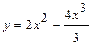 на монотонность и экстремумы, построить график

Вариант 5

Задача. Исследовать функцию 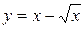  на монотонность и экстремумы, построить график.

Вариант 6

Задача. К источнику постоянного тока с электродвижущейся силой Е  и внутренним сопротивлением 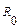подключено внешнее сопротивление 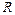. При каком  мощность, выделяемая во внешней цепи, будет максимальной, есл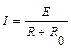и    и 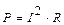? Построить график мощности.

Содержание отчёта

 Отчёт о проделанной работе должен содержать:

- название темы практического занятия;

- цели практического занятия;

- условие задачи;

- подробное решение задачи;

- ответ.

Контрольные вопросы

1. Что можно сказать о движении, если тело движется прямолинейно по закону S=S(t) и  а) S’(t)=1; б)S’(t)=2t?

2. В чём заключается физический и геометрический смысл производной?

3. Как выяснить монотонность функции?

4. Как найти экстремумы функции?

5. Как связана сила тока с величиной заряда, протекающего по проводнику?

Литература:

1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов

Н/Д: Феникс 2014. – 380с.

     2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.

     3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,

         2000 – 560с.

    4. Методическая копилка учителя математики www.metod-kopilka.ru

Практическое занятие № 10