Определенный интеграл численно равен площади криволинейной трапеции, ограниченной сверху кривой y= f( x), 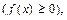 с боков прямыми: x= a и x= b и снизу отрезком [a; b] оси Ox.
с боков прямыми: x= a и x= b и снизу отрезком [a; b] оси Ox.
Значит, площадь криволинейной трапеции, ограниченной кривой y= f( x), 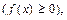 прямыми: x= a и x= b и отрезком [a; b] оси Ox, вычисляется по формуле
прямыми: x= a и x= b и отрезком [a; b] оси Ox, вычисляется по формуле 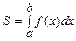 .
.
Площадь фигуры, ограниченной кривыми 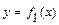 и
и 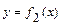
 и прямыми
и прямыми 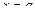 и
и 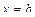 , находится по формуле
, находится по формуле 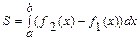 .
.
План вычисления площади плоской фигуры:
1. Построить графики линий, ограничивающих фигуру.
2. Найти пределы интегрирования.
3. Вычислить соответствующий определенный интеграл.
Найти площадь фигуры, ограниченной линиями  и
и 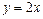 .
.
Решение. Данная фигура ограничена параболой  и прямой
и прямой 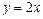 .Найдем точки пересечения заданных линий, решив уравнение
.Найдем точки пересечения заданных линий, решив уравнение 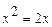 . Корки уравнения
. Корки уравнения 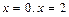 . Используя определенный интеграл, вычислим площадь фигуры
. Используя определенный интеграл, вычислим площадь фигуры 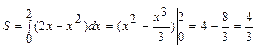 (кв. ед.)
(кв. ед.)
Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью 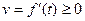 на промежутке от
на промежутке от 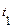 до
до 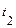 вычисляется по формуле
вычисляется по формуле  .
.
Скорость точки  м/с. Найти путь пройденный точкой за 4-ю секунду.
м/с. Найти путь пройденный точкой за 4-ю секунду.
Решение. По условию 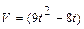 ,
, 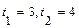 . Следовательно,
. Следовательно, 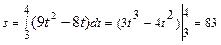 (м).
(м).
Задание
Вариант 1
Задача 1. Скорость прямолинейного движения точки задана формулой 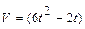 м/с. Найдите закон движения точки, если в момент времени
м/с. Найдите закон движения точки, если в момент времени 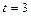 с она находилась на расстоянии 33м от начала движения.
с она находилась на расстоянии 33м от начала движения.
Задача 2. а).Вычислите путь, пройденный телом за три секунды, за вторую секунду, если скорость тела выражается формулой 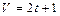 ;
;
б). Вычислите площадь фигуры, ограниченной линиями: 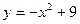 ,
, 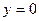 .
.
Вариант 2
Задача 1. Скорость прямолинейного движения точки задана формулой 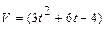 м/с. Найдите закон движения точки, если в момент времени
м/с. Найдите закон движения точки, если в момент времени 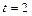 с она находилась на расстоянии 8м от начала движения.
с она находилась на расстоянии 8м от начала движения.
Задача 2. а). Вычислите путь, пройденный телом за три секунды, за вторую секунду, если скорость тела выражается формулой 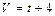 ;
;
б). Вычислите площадь фигуры, ограниченной линиями: 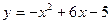 ,
, 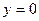 .
.
Вариант 3
Задача 1. Точка движется прямолинейно с ускорением 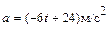 . В момент времени
. В момент времени 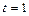 ее скорость равнялась 15 м/с. Найдите закон изменения скорости точки.
ее скорость равнялась 15 м/с. Найдите закон изменения скорости точки.
Задача 2. а). Вычислите путь, пройденный телом за три секунды, за вторую секунду, если скорость тела выражается формулой 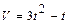 ;
;
б). Вычислите площадь фигуры, ограниченной линиями:  ,
, 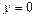 .
.
Вариант 4
Задача 1. Точка движется прямолинейно с ускорением 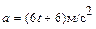 . В момент времени
. В момент времени 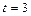 ее скорость равнялась 40 м/с. Найдите закон изменения скорости точки.
ее скорость равнялась 40 м/с. Найдите закон изменения скорости точки.
Задача 2. а). Вычислите путь, пройденный телом за три секунды, за вторую секунду, если скорость тела выражается формулой 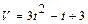 ;
;
б). Вычислите площадь фигуры, ограниченной линиями: 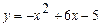 ,
, 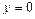 .
.
Вариант 5
Задача 1. Точка движется прямолинейно с ускорением 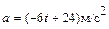 . В момент времени
. В момент времени 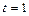 ее скорость равнялась 15 м/с, а пройденный путь 20м. Найдите закон движения точки.
ее скорость равнялась 15 м/с, а пройденный путь 20м. Найдите закон движения точки.
Задача 2. а) Вычислите путь, пройденный телом за три секунды, за вторую секунду, если скорость тела выражается формулой 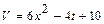 ;
;
б) Вычислите площадь фигуры, ограниченной линиями: 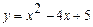 ,
, 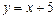 .
.
Вариант 6
Задача 1. Точка движется прямолинейно с ускорением 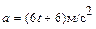 . В момент времени
. В момент времени 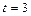 ее скорость равнялась 40 м/с, а при
ее скорость равнялась 40 м/с, а при 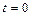 путь
путь 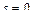 . Найдите закон движении точки.
. Найдите закон движении точки.
Задача 2. а) Вычислите путь, пройденный телом за три секунды, за вторую секунду, если скорость тела выражается формулой 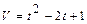 ;
;
б) Вычислите площадь фигуры, ограниченной линиями: 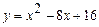 ,
, 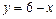 .
.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
6. Как вычислить площадь плоской фигуры?
7. Как по известной скорости находить пройденный путь?
8. Как находить закон движения точки, если известна скорость или ускорение?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 12
Дата: 2019-02-19, просмотров: 340.