Цели: в результате выполнения практической работы, обучающиеся должны уметь разделять переменные, сводить однородное дифференциальное уравнение первого порядка к уравнению с разделяющимися переменными; находить частное решение дифференциального уравнения.

Пояснения к работе

Дифференциальным уравнением с разделяющимися переменными называют дифференциальное уравнение первого порядка вида .

Если перейти к дифференциалам ( 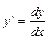), то это уравнение примет вид 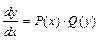. Умножив обе части уравнения на dx, получим уравнение 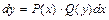. Если разделить последнее уравнение на 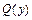, то получим уравнение с разделенными переменными 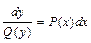, проинтегрировав которое получим общий интеграл .

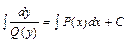Найти общее решение дифференциального уравнения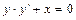

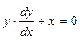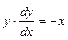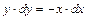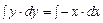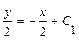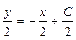Решение: перейдем в данном уравнении к дифференциалам . Перенесем слагаемое х в правую часть уравнения . Умножим обе части уравнения на dx, получим уравнение с разделенными переменными . Проинтегрируем обе части уравнения . Найдем интегралы: . Если обозначить  , то получим уравнение . Умножив обе части на 2, получим общее решение 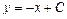. Ответ: .

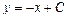Однородным дифференциальным уравнением первого порядка называют дифференциальное уравнение (ДУ) вида .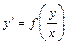

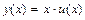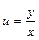Это уравнение приводят к уравнению с разделяющимися переменными относительно новой функции, выполнив следующую замену  или . Тогда  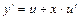и, после подстановки в исходное уравнение полученных выражений, уравнение примет вид 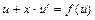. Это уравнение с разделяющимися переменными, разделим переменные 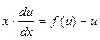; 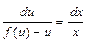. Интегрируя, получим общий интеграл относительно переменных  и . Затем необходимо вернуться к прежним переменным.

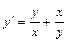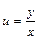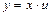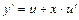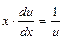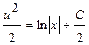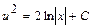Например, найти общее решение ДУ: . Обозначим  или . Тогда  и уравнение примет вид ; ; . Интегрируя, получим ; ; . Вернёмся к прежним переменным 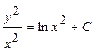. Ответ: .

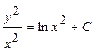Задание

Вариант 1

Задача 1. Найдите общее решение дифференциального уравнения: .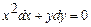

Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 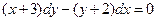, если y = 3 при x = 2.

Вариант 2

Задача 1. Найдите общее решение дифференциального уравнения: .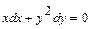

Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 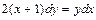, если y = 2 при х =1.

Вариант 3

Задача 1. Найдите общее решение дифференциального уравнения: .

Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 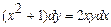, если y = 2 при х = 1.

Вариант 4

Задача 1. Найдите общее решение дифференциального уравнения: .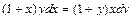

Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 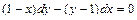, если y = 3 при x = 2.

Вариант 5

Задача 1. Найдите общее решение дифференциального уравнения: .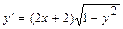

Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 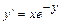, если y = 0 при x = 1.

Вариант 6

Задача 1. Найдите общее решение дифференциального уравнения: .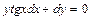

Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 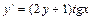, если y = 0 при x = 0.

Содержание отчёта

 Отчёт о проделанной работе должен содержать:

- название темы практического занятия;

- цели практического занятия;

- условие задачи;

- подробное решение задачи;

- ответ.

Контрольные вопросы

1.    Каков алгоритм решения дифференциальных уравнений с разделяющимися переменными?

2.       Что является решением дифференциального решения?

3.    Как находят частное решение дифференциального уравнения с разделяющимися переменными и однородного дифференциального уравнения первого порядка?

Литература:

1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов

Н/Д: Феникс 2014. – 380с.

     2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.

     3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,

         2000 – 560с.

    4. Методическая копилка учителя математики www.metod-kopilka.ru

Практическое занятие № 13