Цели: в результате выполнения практической работы, обучающиеся должны уметь составлять и решать характеристическое уравнение линейного дифференциального уравнения второго порядка с постоянными коэффициентами и применять соответствующую формулу для нахождения общего решения дифференциального уравнения; находить частное решение.
Пояснения к работе
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называют уравнение вида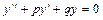 
или 
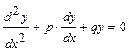, где p и q – постоянные величины.
Для отыскания общего решения данного уравнения составляют характеристическое уравнение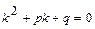 
, которое получается из данного уравнения замено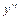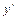й 
, 
и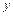 
на соответствующую степень переменной 
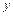, причем сама функция заменяется единицей.
Общее решение данного уравнения строится в зависимости от корней характеристического уравнения. Возможны три случая:
1). Дискриминант уравнения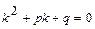 
положительный, т. е. характеристическое уравнение имеет два различных действительных корня 
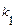и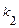 
. В этом случае общее решение уравнения имеет вид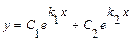 
2). Дискриминант уравнения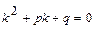 
равен нулю, т. е. характеристическое уравнение имеет два равных действительных корня = = 
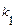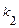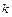. В этом случае общее решение уравнения имеет вид 
.
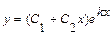3). Дискриминант уравнения 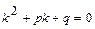отрицательный, т. е. характеристическое уравнение имеет два комплексно-сопряженных корня 
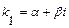и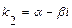 
. В этом случае общее решение уравнения имеет вид 
.
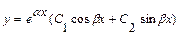Найти частное решение уравнения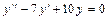 
, если 
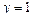и 
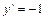при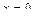 
.
Решение. Составим характеристическое уравнение и найдем его корни 
, 
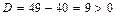, значит, характеристическое уравнение имеет два различных действительных корня: 
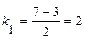и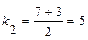 
. Общее решение уравнения имеет вид 
.
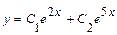Для нахождения искомого частного решения нужно определить значения постоянных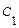 
и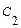 
. Найдем производную общего решения 
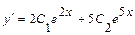. Подставим начальные условия в общее решение и в его производную, получим систему уравнений: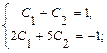 
, 
, 
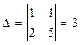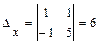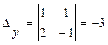. Значит, по формулам Крамера 
, 
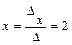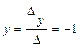. Следовательно, частное решение имеет вид – 
.
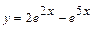Задание
Вариант 1
Задача 1. Найдите общее решение дифференциального уравнения: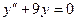 
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 
, если y = 3, y′ = 0 при х = 0.
Вариант 2
Задача 1. Найдите общее решение дифференциального уравнения: 
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: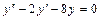 
, если y = 4, y′ = 10 при х = 0.
Вариант 3
Задача 1. Найдите общее решение дифференциального уравнения: 
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: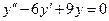 
, если y= 1 и y΄= 1 при х = 0.
Вариант 4
Задача 1. Найдите общее решение дифференциального уравнения: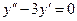 
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: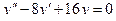 
, если y= 2 и y΄= 9 при х = 0.
Вариант 5
Задача 1. Найдите общее решение дифференциального уравнения: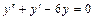 
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: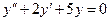 
, если y = 1 и y΄= 1 при х = 0.
Вариант 6
Задача 1. Найдите общее решение дифференциального уравнения: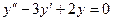 
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 
, если y= 1 и y΄= 5 при х = 0.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Каков алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами?
2. Что является решением дифференциального решения?
3. Как находят частное решение дифференциального уравнения?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 14
Дата: 2019-02-19, просмотров: 203.
