Цель: в результате выполнения практической работы, обучающиеся должны уметь составлять закон распределения случайной величины по условию задачи и находить математическое ожидание случайной величины, дисперсию и среднее квадратическое отклонение.
Пояснения к работе
| Случайными называют величины, которые в результате испытания могут принимать одно и только одно возможное значение, заранее неизвестное и зависящее от случайных причин, которые учесть нельзя. Обозначают СВ – Х, Y , Z . |
| Дискретной называют случайную величину, которая может принимать конечное или бесконечное, но счетное, число значений. Закон распределения СВ – это соответствие между возможными значениями СВ и их вероятностями. |
| Способы задания закона распределения СВ |
| Табличный Таблица, первая строка которой содержит возможные значения СВ, а вторая – их вероятности. | Графический
Линия, координаты точек которой соответственно равны значениям СВ и их вероятностям. Для ДСВ – ломаная, отрезки которой соединяют точки с координатами  .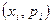
|
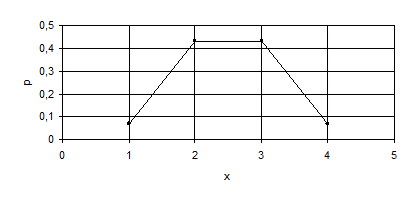
Пример. В партии из 8 деталей 5 стандартных. Наудачу взяты 4 детали. Построить ряд распределения числа стандартных деталей среди отобранных, построить многоугольник распределения вероятностей, задать функцию распределения, построить ее график.
Решение.
| Х | 1 | 2 | 3 | 4 |
| Р |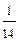 
| 
|
|
|
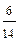
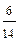
Математическим ожиданием М(х) ДСВХ называют сумму произведений всех ее возможных значений
на их вероятности:  .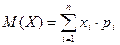
Вероятностный смысл математического ожидания - математическое ожидание – центр распределения.
|
Дисперсией 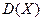 ДСВХ называют математическое ожидание квадрата отклонения СВ от ее математического ожидания М(х)  .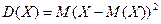
Вероятностный смысл дисперсии: дисперсия СВ – характеристика отклонения (рассеяния) значений данной величины от центра.
|
Средним квадратическим отклонением 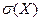 СВХ называют квадратный корень из ее дисперсии
 .
Среднее квадратическое отклонение СВ – характеристика рассеяния значений данной величины от центра.
|
Пример. ДСВХ задана законом распределения:
Х 2 3 5
Р 0,1 0,4 0,5
Найти математическое ожидание случайной величины Х.
Решение. М(Х) =2∙0,1 + 3∙0,4 + 5∙0,5 = 3,9.
Ответ: 3,9.
Пример. Найти дисперсию и среднее квадратическое отклонение ДСВ Х, которая задана законом распределения:
Х 2 3 5
Р 0,1 0,6 0,3
Решение. М(Х) = 2∙0,1 + 3∙0,6 + 5∙0,3 = 3,5. М(Х2) = 4∙0,1 + 9∙0,6 + 25∙0,3 = 13,3. D ( X ) = 13,3 – (3,5)2 = 1,05.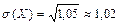 
Ответ: 1,05; 1,02.
Задание
Вариант 1
1. ДСВ задана законом распределения
Х 6 3 1
Р 0,2 0,3 0,5.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Вероятность отказа детали за время испытания на надежность равна 0,3. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 3 деталей.
Вариант 2
1. ДСВ задана законом распределения
Х 2 3 5
Р 0,1 0,4 0,5.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 3 деталей.
Вариант 3
1. ДСВ задана законом распределения
Х 1 2 4
Р 0,1 0,3 0,6.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Вероятность отказа детали за время испытания на надежность равна 0,1. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 4 деталей.
Вариант 4
1. ДСВ задана законом распределения
Х 2 4 8
Р 0,1 0,5 0,4.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Вероятность отказа детали за время испытания на надежность равна 0,1. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 4 деталей.
Вариант 5.
1. ДСВ задана законом распределения
Х 2 10 20 30
Р 0,2 0,3 0,3 0,2 .
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
1. В партии из 6 деталей имеется 3 окрашеных. Наудачу отобраны 3 детали. Найти числовые характеристики дискретной случайной величины Х – числа окрашенных деталей среди отобранных.
Вариант 6.
1. ДСВ задана законом распределения
Х 2 4 8 10
Р 0,1 0,3 0,4 0,2.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. 2. В партии из 10 деталей содержится 3 нестандартных. Наудачу отобраны 2 детали. Найти числовые характеристики дискретной случайной величины
Х – числа нестандартных деталей среди отобранных.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Как вычисляют математическое ожидание случайной величины?
2. В чем заключается вероятностный смысл математического ожидания?
3. Как вычисляют дисперсию случайной величины?
4. В чем заключается вероятностный смысл дисперсии?
5. Как вычисляют среднее квадратическое отклонение случайной величины?
6. В чем заключается вероятностный смысл среднего квадратического отклонения?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 7
Дата: 2019-02-19, просмотров: 284.
