Цели: в результате выполнения практической работы, обучающиеся должны уметь решать задачи на вычисление размещений, сочетаний, перестановок.
Пояснения к работе
Комбинаторика
| - раздел математики, изучающий количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества. | |
|
| |
| Правило суммы Если объект А можно выбрать m способами, а объект В – k способами (не такими как А), то выбрать либо А, либо В можно m + k способами. | Правило произведения Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора А) k способами, то пары объектов А и В можно выбрать mk способами. |
|
| |
| Конечное множество различных элементов – генеральная совокупность без повторений. | |
|
| |
| Произвольная группа элементов данной генеральной совокупности – выборка без повторений. | |
| Виды выборок |
Размещения– выборки,
составленные из n различных элементов генеральной совокупности по m элементов, которые отличаются либо составом элементов, либо их порядком.
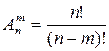
| Перестановки-выборки,
составленные из одних и
тех же n элементов
генеральной совокупности
и отличающиеся
только порядком
их расположения.
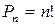
| Сочетания – выборки, составленные из n
различных элементов
генеральной совокупности
по m элементов,
которые отличаются
хотя бы одним элементом.
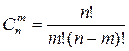
|
| Множество, которое содержит набор n различных классов одинаковых элементов – генеральная совокупность с повторениями. |
| Виды выборок |
Размещения с повторениями – выборки,
составленные из m элементов, выбранных из числа элементов данных n классов генеральной совокупности с повторениями, которые отличаются либо составом элементов, либо их порядком.
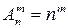
| Размещения с заданным количеством повторений каждого элемента (перестановки) – выборки, которые
отличаются только порядком расположения элементов, когда от i-го класса в каждой выборке участвует 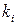 элементов. элементов.
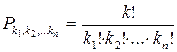 , где , где 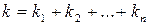
| Сочетания с повторениями – выборки, составленные из m элементов, выбранных из числа элементов данных n классов генеральной совокупности с повторениями,
которые отличаются
хотя бы одним элементом.
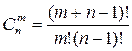
|
Размещения и перестановки – упорядоченные выборки, а сочетания – неупорядоченные выборки.
Символ n! (читается: «эн факториал») есть сокращенное обозначение произведения 1·2·3·…·(n -1)·n.
Принято считать 0! = 1 и 1! = 1.
Примеры.
1. На тренировках занимаются 12 баскетболистов. Сколько может быть образовано тренером разных стартовых пятерок?
Решение. Так как при составлении стартовой пятерки тренера интересует только состав пятерки, то достаточно определить число сочетаний из 12 элементов по 5:
С 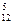 =
= 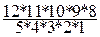 = 792.
= 792.
2. Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг друга?
Решение. Ясно, что в этом случае на каждой горизонтали и каждой вертикали шахматной доски может быть расположено только по одной ладье. Число возможных позиций – число перестановок из 8 элементов:
Р8 = 8! = 8*7*6*5*4*3*2*1 = 40 320.
3. Для полета на Марс необходимо укомплектовать следующий экипаж космического корабля: командир корабля, первый его помощник, второй помощник, два бортинженера и один врач. Командующая тройка может быть отобрана из числа 25 готовящихся к полету летчиков, два борт инженера – из числа20 специалистов, в совершенстве знающих устройство космического корабля, и врач – из числа 8 медиков. Сколькими способами можно укомплектовать экипаж исследователей космоса?
Решение. При выборе командира и его помощников важно определить, какой из военных летчиков лучше других справляется с теми или иными функциями в управлении кораблем. Значит, здесь важен не только персональный состав командующей тройки, но и соответствующая расстановка подобранных людей. Поэтому ясно, что командующая тройка может быть укомплектована А 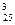 способами.
способами.
Обязанности у обоих бортинженеров примерно одинаковые. Они могут выполнять их по очереди. Следовательно, пара бортинженеров может быть укомплектована С 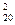 способами. Аналогичное положение и с врачом – его можно подобрать С
способами. Аналогичное положение и с врачом – его можно подобрать С 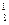 способами.
способами.
В силу правила произведения весь экипаж может быть укомплектован
А 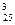 *С
*С 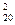 *С
*С 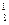 =20976000 способами.
=20976000 способами. 
Задание
Вариант1
1. Профсоюзная организация техникума насчитывает 150 членов. Сколькими способами можно выбрать 6 делегатов на городскую конференцию?
2. Из цифр 1,2,3,4 составлены все возможные двузначные числа, при условии, что: в каждом числе нет одинаковых цифр; цифры в числе могут быть одинаковыми. Сколько получилось чисел?
3. Сколько разных слов можно образовать при перестановке слова «комбинаторика»?
Вариант 2
1. Группа студентов изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть четыре различных урока?
2. Сколькими способами можно выбрать гласную и согласную буквы из слова «полка»?
3. В гастрономе имеются конфеты четырех наименований. Конфеты упакованы в коробки четырех видов – для каждого наименования своя коробка. Сколькими способами можно заказать набор из 6 коробок.
Вариант 3
1. Из цифр 0, 1, 2, 3 составлены все возможные трехзначные числа так, что в каждом числе нет одинаковых цифр; цифры могут быть одинаковые. Сколько получилось чисел?
2. Во взводе 3 сержанта и 30 солдат. Сколькими способами можно выделить одного сержанта и трех солдат для патрулирования?
3. Сколько разных слов можно образовать при перестановке букв слова «соединение»?
Вариант 4
1. Сколько чисел, меньших миллиона, можно записать с помощью цифр 8 и 9?
2. На 5 сотрудников выделено 3 путевки. Сколькими способами их можно распределить, если: все путевки различные; все путевки одинаковые?
3. Для несения почетного караула из 10 человек могут быть приглашены офицеры пехотных войск, авиации, пограничных войск, артиллерии, офицеры морского флота и ракетных войск. Сколькими способами можно избрать состав почетного караула?
Вариант 5
1. Пусть из пункта A в пункт B имеется 5 дорог, а из пункта B в пункт C – 6 дорог. Сколько существует различных вариантов проезда из пункта A в пункт C?
2. В коробке находятся 50 деталей, из которых 10 бракованных. Из коробки наудачу берутся 5 деталей. Найти число различных способов взятия 5-ти деталей, среди которых ровно 3 бракованных.
3. На полке наудачу располагаются 10 книг. Сколько существует различных способов расположения 10-ти книг? Сколько существует различных способов расположения 10-ти книг, при которых 2 заранее помеченные книги окажутся рядом?
Вариант 6
1. Сколько разных четырехзначных чисел можно составить из цифр 0, 1,2,если та же самая цифра может повторяться несколько раз?
2. Сколько можно изготовить трехцветных флажков, если для этого использовать следующие цвета: белый, синий, красный, желтый, зеленый, черный?
3. На студенческий вечер собрались ребята 1, 2, 3 курсов. Вести вечер приглашаются 10 студентов. Сколькими способами можно выбрать ведущих при условии участия в нем хотя бы одного третьекурсника?
Контрольные вопросы.
1. Что изучает комбинаторика?
2. Сформулируйте правило суммы и правило произведения.
3. Чему равен факториал n?
4. Чем отличаются упорядоченные выборки от неупорядоченных выборок?
5. По каким формулам рассчитывают размещения?
6. По каким формулам рассчитывают сочетания?
7. По каким формулам рассчитывают перестановки?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 5
Дата: 2019-02-19, просмотров: 931.