С использованием теорем сложения и умножения вероятностей
Цель: в результате выполнения практической работы, обучающиеся должны уметь применять теоремы умножения и сложения вероятностей для вычисления вероятности сложных событий.
Пояснения к работе
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.
А + В = С ( 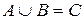 ). ).
| Произведением (или пересечением) нескольких событий называют событие, состоящее в одновременном наступлении всех этих событий в результате испытания.
А·В = С ( 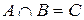 ) )
| Противоположными называют два единственно возможных события, образующих полную группу.
А и 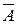 - противоположные события. - противоположные события.
|
Пусть А, В и С – случайные события, выраженные элементарными событиями одного и того же пространства элементарных событий. Тогда следующие события можно записать формулами:
а) событие «произошло только А» записывается формулой 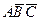 ;
;
б) событие «произошло одно и только одно из данных событий» записывается формулой  +
+ 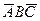 +
+  ;
;
в) событие «произошли два и только два из данных событий» записывается формулой 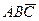 +
+ 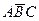 +
+ 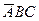 ;
;
г) событие «произошли все три события» записывается формулой 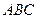 ;
;
д) событие «произошло хотя бы одно из данных событий» записывается формулой А + В + С;
е) событие «произошло не боле двух событий» записывается формулой 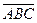 .
.
| Теоремы сложения вероятностей |
Вероятность появления хотя бы одного из двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления. 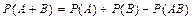
|
Р(АВ) = 0, если события несовместны.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
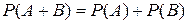
|
Сумма вероятностей противоположных событий равна единице.
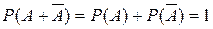
|
Вероятность появления хотя бы одного из событий А1, А2, …, А n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий. 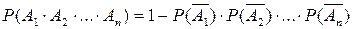
|
| Теоремы умножения вероятностей |
Условной вероятностью события В при условии А называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
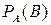 или или 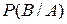
|
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое уже произошло.
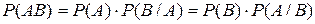
|
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий. 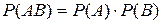 . .
|
| Событие В называют независимым от события А, если появление события А не изменяет вероятности появления события В. |
Пример 1. Вероятность того, что день будет дождливым, р = 0,7. Найти вероятность того, что день будет ясным.
Решение. События «день дождливый» и «день ясный» - противоположные, поэтому искомая вероятность q = 1 – p = 1 – 0,7 =0,3.
Ответ: 0,3.
Пример 2. Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны: 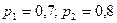 . Найти вероятность попадания при одном залпе (из двух орудий) хотя бы одним из орудий.
. Найти вероятность попадания при одном залпе (из двух орудий) хотя бы одним из орудий.
Решение. Попадание в цель одним из орудий не исключает возможности попадания в цель другим орудием. Значит, события А – «попадание первого орудия» и В – «попадание второго орудия» совместны. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А и В независимы. А поэтому Р(А+В) = Р(А) + Р(В) – Р(А)·Р(В) = 0,7 + 0,8 – 0,7·0,8 = 0,94.
Ответ: 0,94.
Пример 3. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными. 
Решение. Вероятность того, что из первого ящика вынута стандартная деталь (событие А), Р(А) = 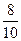 = 0,8. Вероятность того, что из второго ящика вынута стандартная деталь (событие В), Р(В) =
= 0,8. Вероятность того, что из второго ящика вынута стандартная деталь (событие В), Р(В) =  = 0,7. Вероятность того, что из третьего ящика вынута стандартная деталь (событие С), Р(С) =
= 0,7. Вероятность того, что из третьего ящика вынута стандартная деталь (событие С), Р(С) = 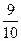 = 0,9. Так как события А, В и С независимы в совокупности, то искомая вероятность (по теореме умножения) равна Р(АВС) = Р(А)Р(В)Р(С) = 0,8∙0,7∙0,9 =0,504.
= 0,9. Так как события А, В и С независимы в совокупности, то искомая вероятность (по теореме умножения) равна Р(АВС) = Р(А)Р(В)Р(С) = 0,8∙0,7∙0,9 =0,504.
Ответ: 0,504.
Задание
Вариант 1
1. Для сигнализации об аварии установлены 2 независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найдите вероятность того, что при аварии:
а) ни один не сработает;
б) сработает хотя бы один;
в) оба сработают.
2. Вероятность того, что Таня на экзамене получит «5», равна 0,6. Найдите вероятность того, что Таня ответит меньше «5».
Вариант 2
1. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго 0,8. Найдите вероятность того, что при одном залпе в мишень:
а) ни один не попал;
б) хотя бы один попал;
в) оба попали.
2. В экзаменационном билете 3 вопроса. Вероятность того, что студент знает все три вопроса билета, равна 0,4. Найдите вероятность того, что студент знает менее трех вопросов билета.
Вариант 3
1. В двух ящиках находятся детали: в первом – 10 (из них 3 стандартных), во втором – 15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найдите вероятность того, что:
а) обе детали окажутся нестандартными;
б) хотя бы одна деталь стандартная;
в) обе детали стандартные.
2. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенный ему экзаменатором вопрос.
Вариант 4
1. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены два независимых измерения. Найдите вероятность того, что:
а) в двух из них допущена ошибка, превысит заданную точность;
б) хотя бы в одном превысит заданную точность;
в) ни в одном превысит заданную точность.
2. В цехе работают 7 мужчин и три женщины. По табельным номером наудачу отобраны 2 человека. Найти вероятность того, что отобраны мужчина и женщина.
Вариант 5
1. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найдите вероятность того, что из двух проверенных изделий:
а) ни одно не оказалось высшего сорта;
б) хотя бы одно высшего сорта;
в) оба высшего сорта.
2. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что наудачу выбранный билет окажется выигрышным.
Вариант 6
1. Рабочий обслуживает 2 станка, каждый из которых работает независимо один от другого. Вероятность того, что за смену станки не потребуют вмешательства рабочего равны соответственно р1 = 0,3, р2 = 0,2. Найдите вероятность того, что за смену:
а) ни один не потребует вмешательства;
б) хотя бы один станок потребует вмешательства рабочего;
в) оба потребуют вмешательства.
2. В читальном зале имеется шесть учебников по теории вероятности, из которых три в переплете. Библиотекарь берет наудачу учебник. Найдите вероятность того, что он окажется в переплете.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы.
1. Как находить вероятность суммы, произведения событий?
2. Чему равна вероятность достоверного события, невозможного события, случайного события?
3. Какие события называют несовместными, независимыми?
4. Как определяется произведение событий? Какие теоремы умножения вероятностей вы знаете?
5. Как определяются противоположные события? Как вычислить вероятности противоположных событий?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 6
Дата: 2019-02-19, просмотров: 412.