Цели: в результате выполнения практической работы, обучающиеся должны уметь строить графы, записывать матрицы, решать задачи.
Пояснения к работе
Определение. Если на плоскости задать конечное множество V точек и конечный набор линий Х, соединяющих некоторые пары из точек V, то полученная совокупность точек и линий будет называться графом.
При этом элементы множества V называются вершинами графа, а элементы множества Х – ребрами.
В множестве V могут встречаться одинаковые элементы, ребра, соединяющие одинаковые элементы называются петлями. Одинаковые пары в множестве Х называются кратными (или параллельными) ребрами. Количество одинаковых пар
(v, w) в Х называется кратностью ребра (v, w).
Множество V и набор Х определяют граф с кратными ребрами – псевдограф.
G = ( V, X)
Псевдограф без петель называется мультиграфом.
Если в наборе Х ни одна пара не встречается более одного раза, то мультиграф называется графом.
Если пары в наборе Х являются упорядочными, то граф называется ориентированным или орграфом.
Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины.
Определение. Если х = {v, w} – ребро графа, то вершины v, w называются концами ребра х.
Если х = ( v, w) – дуга орграфа, то вершина v – начало, а вершина w – конец дуги х.
Определение. Вершины v, w графа G = (V, X) называются смежными, если {v, w}ÎX. Два ребра называются смежными, если они имеют общюю вершину.
Определение. Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется изолированной, если ее степень равна единице и висячей, если ее степень равна нулю.
Определение. Графы G1(V1, X1) и G2(V2, X2) называются изоморфмными, если существует взаимно однозначное отображение j: V1 ® V2, сохраняющее смежность.
Определение. Маршрутом (путем) для графа G(V, X) называется последовательность v1x1v2x2v3…xkvk+1. Маршрут называется замкнутым, если его начальная и конечная точки совпадают. Число ребер (дуг) маршрута (пути) графа называется длиной маршрута (пути).
Определение. Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.
Определение. Замкнутый маршрут (путь) называется циклом (контуром). Цикл, в котором все вершины попарно различны, называется простым циклом.
Матрицы графов.
Пусть D = (V, X) – орграф, где V = {v1, …, vn}, X = {x1, … , xm}.
Определение. Матрицей смежности орграфа D называется квадратичная матрица A(D) = [aij] порядка п, у которой
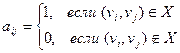
Определение. Если вершина v является концом ребра х, то говорят, что v и х – инциндентны.
Определение. Матрицей инциндентности оргафа D называется матрица размерности п´т B(D) = [bij], у которой
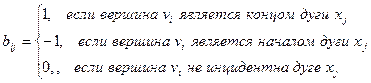
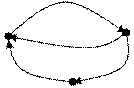
Пример. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.
x1
v1 x4 v2
x2
x3
v3
Составим матрицу смежности:
| v1 | v2 | v3 | |
| v1 | 0 | 1 | 0 |
| v2 | 1 | 0 | 1 |
| v3 | 1 | 0 | 0 |
Т.е.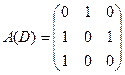 
- матрица смежности.
Матрица инциндентности:
| x1 | x2 | x3 | x4 | |
| v1 | -1 | 0 | 1 | 1 |
| v2 | 1 | -1 | 0 | -1 |
| v3 | 0 | 1 | -1 | 0 |
Т.е. 
Если граф имеет кратные дуги (ребра), то в матрице смежности принимается aij= k, где k – кратность дуги (ребра).
С помощью матриц смежности и инциндентности всегда можно полностью определить граф и все его компоненты. Такой метод задания графов очень удобен для обработки данных на ЭВМ.
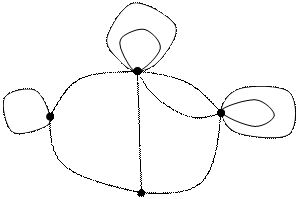
Пример. Задана симметрическая матрица Q неотрицательных чисел. Нарисовать на плоскости граф G(V, X), имеющий заданную матицу Q своей матрицей смежности. Найти матрицу инциндентности R графа G. Нарисовать также орграф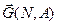 
, имеющий матрицу смежности Q, определить его матрицу инциндентности С.
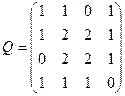
x4
x3
v2
x2 x5
x6
x1 v1 v3 x7 x8
x10
x11 x9
v4
Составим матрицу инциндентности:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | |
| v1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| v2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| v3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| v4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Итого: 
Построим теперь ориентированный граф с заданной матрицей смежности.
x4
x5
 |
v2
x2 x7
х3 x6
x1 v1 х8 v3 x10 x11
х9
х17 х15 x14
x16 х13 x12
v4
Составим матрицу инциндентности для ориетированного графа.
Элемент матрицы равен 1, если точка является концом дуги, -1 – если началом дуги, если дуга является петлей, элемент матрицы запишем как ±1.
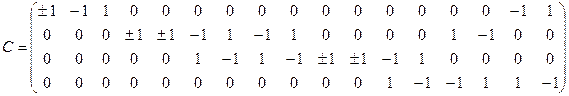
Таким образом, операции с графами можно свести к операциям с их матрицами.
Задание
Вариант 1.
Задача1.Ориентированный граф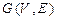 
с множеством вершин 
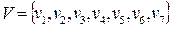задан списком дуг 
.
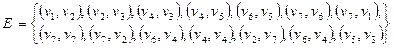Построить реализацию графа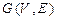 
. Построить матрицу смежности и матрицу инцидентности графа 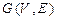. Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 9 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 2.
Задача1.Ориентированный граф 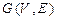с множеством вершин 
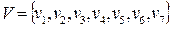задан списком дуг 
.
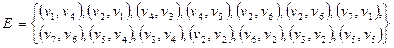Построить реализацию графа 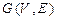. Построить матрицу смежности и матрицу инцидентности графа 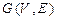. Укажите степени вершин графа.
Задача2. Решите задачу, решение представьте в виде графа: из 27 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 3.
Задача1.Ориентированный граф 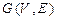с множеством вершин 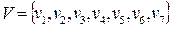задан списком дуг 
.
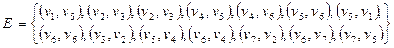Построить реализацию графа 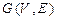. Построить матрицу смежности и матрицу инцидентности графа 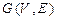. Укажите степени вершин графа.
Задача 3. Решите задачу, решение представьте в виде графа: из 18 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 4.
Задача1.Ориентированный граф 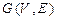с множеством вершин 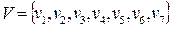задан списком дуг 
.
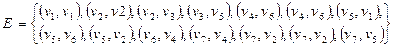Построить реализацию графа 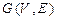. Построить матрицу смежности и матрицу инцидентности графа 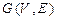. Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 12 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 5.
Задача1.Ориентированный граф 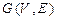с множеством вершин 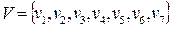задан списком дуг 
.
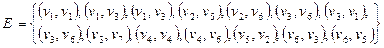Построить реализацию графа 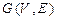. Построить матрицу смежности и матрицу инцидентности графа 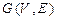. Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 15 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 6.
Задача1.Ориентированный граф 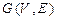с множеством вершин 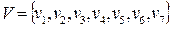задан списком дуг 
.
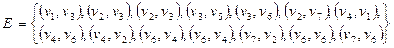Построить реализацию графа 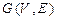. Построить матрицу смежности и матрицу инцидентности графа 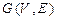. Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 21 монеты одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Графы являются «топологическими» или «геометрическими» объектом.
2. Каково соотношение между количествами вершин, рёбер и граней в плоском графе.
3. Приведите простейшие примеры неплоских графов.
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 4
Дата: 2019-02-19, просмотров: 493.
