Цели: в результате выполнения практической работы, обучающиеся должны уметь решать системы линейных алгебраических уравнений по формулам Крамера.
Пояснения к работе
Системой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида
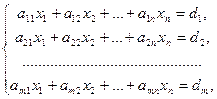
где числа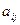 
, 
, 
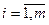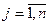называют коэффициентами системы, числа 
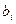- свободными членами,
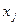- неизвестные.
Такую систему принято записывать в компактной матричной форме А∙Х=В.
А- матрица коэффициентов системы, называемая основной матрицей:
А =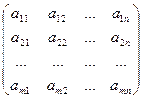 
, Х = 
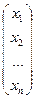- вектор-столбец из неизвестных ,
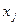В =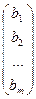 
- вектор-столбец из свободных чисел .
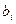Произведение матриц А∙Х определено, т. к. в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
Решением системы называется n значений неизвестных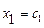 
, 
, …, 
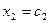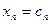, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде вектор-столбца С = 
.
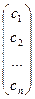Пусть дана система n линейных уравнений с n неизвестными
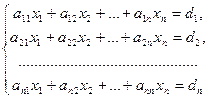
или в матричной форме А∙Х=В.
Основная матрица такой системы квадратная. Определитель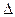 
такой матрицы называется определителем системы. Если определитель системы отличен от нуля 
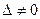, то система имеет единственное решение.
Найдем решение данной системы в случае .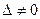
Умножив обе части уравнения А∙Х=В слева на матрицу 
(матрица обратная матрице А), получим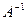 
∙ А∙Х = 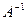∙В. Поскольку
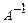∙ А = Е и Е∙Х = Х, то Х = 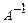∙В. (1)
Отыскание решения системы по формуле (1) называется матричным способом решения системы.
Формулы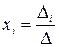 
, 
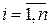или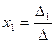 
, 
, …, 
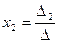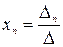называются формулами Крамера, где
, 
,
,…, 
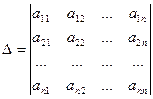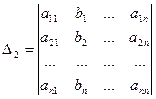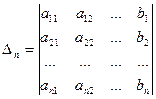
Примеры:.
1. Решить по формулам Крамера систему уравнений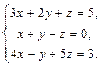 
Для того, чтобы решить систему уравнений по формулам Крамера вычислим определитель системы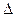 
и определители 
, 
, 
.
, 
, 
, 
.
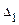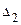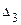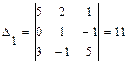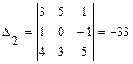По формулам Крамера найдем значения переменных.
, 
, 
.
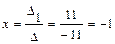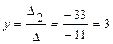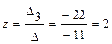Ответ: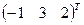 
.
Задание
Вариант 1
Задача . Решить систему по формулам Крамера а)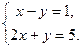 
б)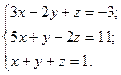 
Вариант 2
Задача . Решить систему по формулам Крамера а)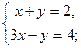 
б)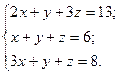 
Вариант 3
Задача. Решить систему по формулам Крамера а)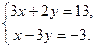 
б) 
Вариант 4
Задача . Решить систему по формулам Крамера а)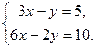 
б) 
Вариант 5
Задача . Решить систему по формулам Крамера а)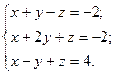 
б) 
Вариант 6
Задача . Решить систему по формулам Крамера а)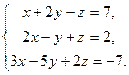 
б)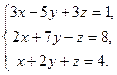 
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. При каком условии однородная система имеет нулевые решения?
2. Для каких систем применимо правило Крамера?
3. Как составляют определители при решении систем линейных алгебраических уравнений по формулам Крамера?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 3
Дата: 2019-02-19, просмотров: 203.
