МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ ОБУЧАЮЩИХСЯ ПО ПРОВЕДЕНИЮ
ПРАКТИЧЕСКИХ ЗАНЯТИЙ
для специальности
13.02.11 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)»
Учебная дисциплина
«МАТЕМАТИКА»
Смоленск
Г.
Рассмотрено и одобрено
ЦМК общеобразовательных дисциплин
Предс. ЦМК
____________ /Гмырикова С.В./
Протокол №______
«___»___________20__г.
Составитель: Абрамова Г.М., преподаватель ОГБПОУ «Смоленский политехнический техникум»
Рецензент: Филипенко И.В., преподаватель ОГБПОУ «Смоленский политехнический техникум»
Методические указания для обучающихся по проведению практических занятий являются частью основной профессиональной образовательной программы ОГБПОУ «Смоленский политехнический техникум» по специальности 13.02.11 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)» в соответствии с требованиями федеральных государственных образовательных стандартов третьего поколения (далее – ФГОС).
Методические указания для обучающихся по проведению практических занятий включают в себя предисловие, цели работы, пояснения к работе, задание, порядок и образец отчёта, контрольные вопросы, литературу, приложения.
СОДЕРЖАНИЕ
| Номер, название практических занятий | Страницы |
| Практическое занятие №1 «Действия с матрицами» | 5 |
| Практическое занятие №2 «Решение системы линейных уравнений по формулам Крамера » | 8 |
| Практическое занятие №3 «Построение графов. Решение задач c использованием графов.» | 11 |
| Практическое занятие №4 «Решение задач на вычисление размещений, сочетаний, перестановок » | 16 |
| Практическое занятие №5 «Решение простейших задач на определение вероятности с использованием теоремы сложения и умножения вероятностей » | 18 |
| Практическое занятие №6 «Построение распределения дискретной случайной величины по заданному условию.» | 21 |
| Практическое занятие №7 «Вычисление пределов функций различными методами.» | 24 |
| Практическое занятие №8 «Дифференцирование функций. Вычисление производной сложных функций.» | 27 |
| Практическое занятие №9 «Исследование функций с помощью первой и второй производных и построение графиков функций. » | 29 |
| Практическое занятие №10 «Вычисление определенного интеграла » | 32 |
| Практическое занятие №11 «Вычисление площадей фигур, решение задач физического содержания с помощью определённого интеграла.» | 36 |
| Практическое занятие №12 «Решение дифференциальных уравнений с разделяющимися переменными.» | 38 |
| Практическое занятие№13 «Решение линейных однородных уравнений второго порядка с постоянными коэффициентами.» | 39 |
| Практическое занятие №14 «Исследование числовых рядов на сходимость. Определение сходимости рядов по признаку Даламбера.» | 41 |
| Практическое занятие №15 «Численное интегрирование. Формулы прямоугольников, формула Симпсона. Формула трапеций.» | 45 |
ПРЕДИСЛОВИЕ
УВАЖАЕМЫЕ СТУДЕНТЫ!
Методические указания для обучающихся по проведению практических занятий по учебной дисциплине «Математика» созданы вам в помощь для работы на занятиях, правильного составления отчётов. Приступая к выполнению задания, вы должны внимательно прочитать цели, ознакомиться с пояснениями к работе, содержащими краткие теоретические сведения по теме работы и методические рекомендации, ответить на контрольные вопросы.
Практическое занятие содержит задание, состоящее из шести вариантов, включающих задачи, соответствующие указанным в ФГОС требованиям к уровню вашей подготовки. Выполнять задание, делать выводы по проделанной работе вы должны согласно инструкции преподавателя.
Отчёт о работе вы должны оформить по приведённому образцу.
Наличие положительных оценок по практическим занятиям необходимо для допуска к дифференцированному зачету по учебной дисциплине «Математика». В случае отсутствия на учебном занятии по любой причине или получения неудовлетворительной оценки за практическое занятие вы должны выполнить работу или пересдать.
ВНИМАНИЕ! В результате выполнения заданий практических занятий по УД «Математика» вы освоите умения
- решать прикладные задачи в области профессиональной деятельности,
на основе знаний:
– значения математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
- основных математических методов решения прикладных задач в области профессиональной деятельности;
- основных понятий и методов математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
- основ интегрального и дифференциального исчисления.
Желаем вам успехов!
Практическое занятие № 1
Действия с матрицами
Цели: в результате выполнения практической работы, обучающиеся должны уметь выполнять действия с матрицами.
Пояснения к работе
Теоретические сведения:
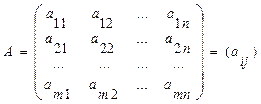 - матрица размера m × n ( i = 1, m, j = 1, n).
- матрица размера m × n ( i = 1, m, j = 1, n).
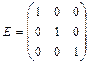 - единичная матрица,
- единичная матрица, 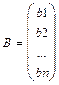 - вектор-столбец,
- вектор-столбец,
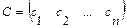 -вектор-строка.
-вектор-строка.
Каждой квадратной матрице (размера n × m) можно поставить в соответствие определённое число, которое называют определителем матрицы.
Ат = 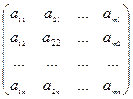 -транспонированная матрица.
-транспонированная матрица.
Матрица А называется невырожденной, если определитель ∆А ≠ 0, в противном случае матрица А называется вырожденной.
А*= 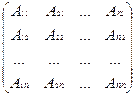 - союзная матрица, А ij – алгебраическое дополнение элемента aij.
- союзная матрица, А ij – алгебраическое дополнение элемента aij.
А-1 называется матрицей обратной матрице А, если выполняется условие
А∙А-1 = А∙А-1 = Е.
Всякая невырожденная матрица имеет себе обратную: А-1= 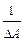 А*.
А*.
Рассмотрим матрицу А m× n.  .
.
Выделим в ней k строк и столбцов k столбцов. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы, обозначают r( A).
Примеры: 1.Найдите значение матричного многочлена 2А2 + 4АВ - 3Е, если Е единичная матрица второго порядка и 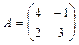 ,
, 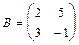 .
.
Решение:
Найдем 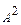 :
: 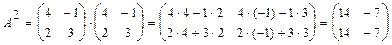 .
.
Умножим 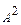 на 2:
на 2:  .
.
Найдем произведение матриц  :
: 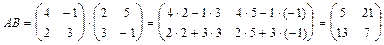 .
.
Найдем значение выражения 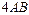 :
: 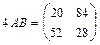 .
.
Найдем произведение единичной матрицы на 3: 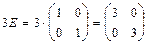 .
.
Найдем значение выражения 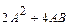 :
: 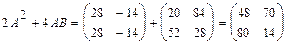 .
.
Найдем значение выражения 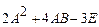 :
: 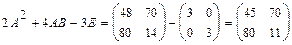 .
.
Ответ: 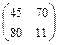 .
.
2. Найти матрицу обратную данной, сделать проверку:
Найти 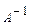 , если
, если 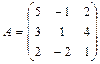 .
.
Решение:
Найдем  :
: 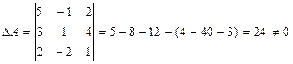 . Матрица невырожденная.
. Матрица невырожденная.
Найдем  :
:
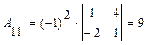 ;
; 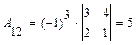 ;
; 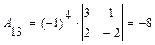 ;
;
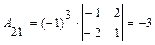 ;
; 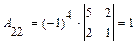 ;
; 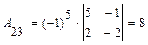 ;
;
 ;
; 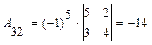 ;
; 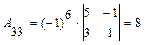 ,
,
поэтому 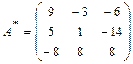 .
.
Найдем 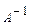 :
: 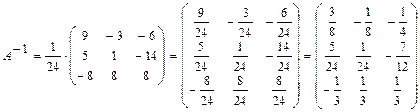 .
.
Проверка: А  .
.
3. Определить ранг матрицы:  .
.
Решение:
Приведем данную матрицу к каноническому виду, для чего выполним три действия: умножим первую строку на -4 и сложим с второй строкой; умножим первую строку на -2 и сложим с третьей строкой; умножим первую строку на 5 и сложим с четвертой строкой. 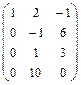 Выполним два действия: умножим первый столбец на -2 и сложим со вторым, а затем сложим первый и третий столбцы.
Выполним два действия: умножим первый столбец на -2 и сложим со вторым, а затем сложим первый и третий столбцы. 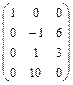 . Поменяем местами вторую и третью строки.
. Поменяем местами вторую и третью строки. 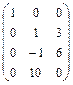 . Умножим второй столбец на -3 и сложим с третьим столбцом.
. Умножим второй столбец на -3 и сложим с третьим столбцом. 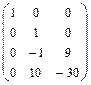 Выполним два действия: сложим вторую и третью строки; умножим вторую строку на -10 и сложим с четвертой строкой.
Выполним два действия: сложим вторую и третью строки; умножим вторую строку на -10 и сложим с четвертой строкой. 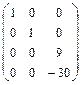 .Разделим 3, 4 строки соответственно на 9, 30.
.Разделим 3, 4 строки соответственно на 9, 30. 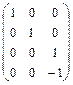 . Сложим третью и четвертую строки.
. Сложим третью и четвертую строки. 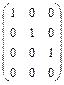 . Значит,
. Значит, 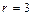 .
.
Задание
Найдите значение матричного многочлена 2А2 + 3В + 5Е, если Е единичная матрица третьего порядка.
1в 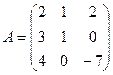 ,
,  . 2в
. 2в 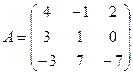 ,
, 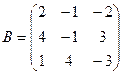 .
.
3в 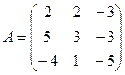 ,
, 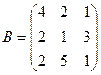 . 4в
. 4в 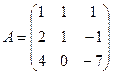 ,
, 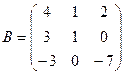 .
.
5в 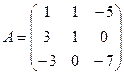 ,
, 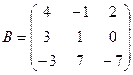 . 6в
. 6в 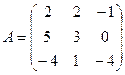 ,
, 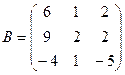 .
.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Что называют матрицей? Нулевой матрицей?
2. Какие матрицы называют равными?
3. Какую матрицу называют квадратной? Единичной?
4. Какую матрицу называют вектором?
5. Что является суммой двух матриц? Произведением матрицы на число?
6. Какую матрицу называют противоположной?
7. Сформулировать свойства операций сложения матриц, умножения матрицы на число.
8. Что называют произведением двух матриц? Всегда ли можно найти произведение двух матриц?
9. Сформулировать свойства умножения матриц.
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 2
Пояснения к работе
Системой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида
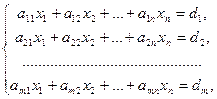
где числа 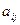 ,
, 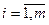 ,
, 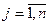 называют коэффициентами системы, числа
называют коэффициентами системы, числа 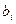 - свободными членами,
- свободными членами,
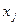 - неизвестные.
- неизвестные.
Такую систему принято записывать в компактной матричной форме А∙Х=В.
А- матрица коэффициентов системы, называемая основной матрицей:
А = 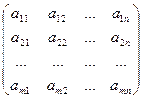 , Х =
, Х = 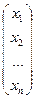 - вектор-столбец из неизвестных
- вектор-столбец из неизвестных 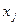 ,
,
В = 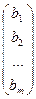 - вектор-столбец из свободных чисел
- вектор-столбец из свободных чисел 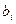 .
.
Произведение матриц А∙Х определено, т. к. в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
Решением системы называется n значений неизвестных 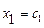 ,
, 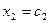 , …,
, …, 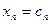 , при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде вектор-столбца С =
, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде вектор-столбца С = 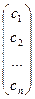 .
.
Пусть дана система n линейных уравнений с n неизвестными
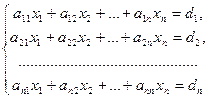
или в матричной форме А∙Х=В.
Основная матрица такой системы квадратная. Определитель 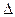 такой матрицы называется определителем системы. Если определитель системы отличен от нуля
такой матрицы называется определителем системы. Если определитель системы отличен от нуля 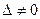 , то система имеет единственное решение.
, то система имеет единственное решение.
Найдем решение данной системы в случае 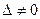 .
.
Умножив обе части уравнения А∙Х=В слева на матрицу  (матрица обратная матрице А), получим
(матрица обратная матрице А), получим 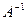 ∙ А∙Х =
∙ А∙Х = 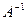 ∙В. Поскольку
∙В. Поскольку
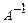 ∙ А = Е и Е∙Х = Х, то Х =
∙ А = Е и Е∙Х = Х, то Х = 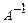 ∙В. (1)
∙В. (1)
Отыскание решения системы по формуле (1) называется матричным способом решения системы.
Формулы 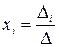 ,
, 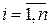 или
или 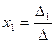 ,
, 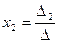 , …,
, …, 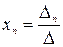 называются формулами Крамера, где
называются формулами Крамера, где
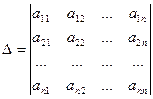 ,
,  ,
,
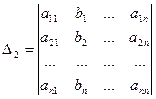 ,…,
,…, 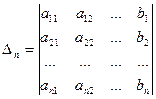
Примеры:.
1. Решить по формулам Крамера систему уравнений 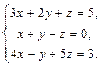
Для того, чтобы решить систему уравнений по формулам Крамера вычислим определитель системы 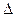 и определители
и определители 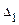 ,
, 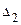 ,
, 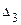 .
.
 ,
, 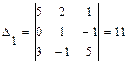 ,
, 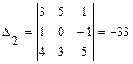 ,
,  .
.
По формулам Крамера найдем значения переменных.
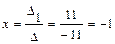 ,
, 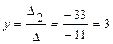 ,
, 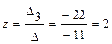 .
.
Ответ: 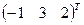 .
.
Задание
Вариант 1
Задача . Решить систему по формулам Крамера а) 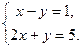 б)
б) 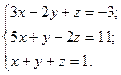
Вариант 2
Задача . Решить систему по формулам Крамера а) 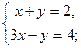 б)
б) 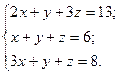
Вариант 3
Задача. Решить систему по формулам Крамера а) 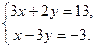 б)
б) 
Вариант 4
Задача . Решить систему по формулам Крамера а) 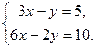 б)
б) 
Вариант 5
Задача . Решить систему по формулам Крамера а) 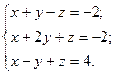 б)
б) 
Вариант 6
Задача . Решить систему по формулам Крамера а) 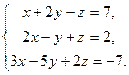 б)
б) 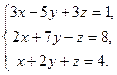
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. При каком условии однородная система имеет нулевые решения?
2. Для каких систем применимо правило Крамера?
3. Как составляют определители при решении систем линейных алгебраических уравнений по формулам Крамера?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 3
Пояснения к работе
Определение. Если на плоскости задать конечное множество V точек и конечный набор линий Х, соединяющих некоторые пары из точек V, то полученная совокупность точек и линий будет называться графом.
При этом элементы множества V называются вершинами графа, а элементы множества Х – ребрами.
В множестве V могут встречаться одинаковые элементы, ребра, соединяющие одинаковые элементы называются петлями. Одинаковые пары в множестве Х называются кратными (или параллельными) ребрами. Количество одинаковых пар
(v, w) в Х называется кратностью ребра (v, w).
Множество V и набор Х определяют граф с кратными ребрами – псевдограф.
G = ( V, X)
Псевдограф без петель называется мультиграфом.
Если в наборе Х ни одна пара не встречается более одного раза, то мультиграф называется графом.
Если пары в наборе Х являются упорядочными, то граф называется ориентированным или орграфом.
Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины.
Определение. Если х = {v, w} – ребро графа, то вершины v, w называются концами ребра х.
Если х = ( v, w) – дуга орграфа, то вершина v – начало, а вершина w – конец дуги х.
Определение. Вершины v, w графа G = (V, X) называются смежными, если {v, w}ÎX. Два ребра называются смежными, если они имеют общюю вершину.
Определение. Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется изолированной, если ее степень равна единице и висячей, если ее степень равна нулю.
Определение. Графы G1(V1, X1) и G2(V2, X2) называются изоморфмными, если существует взаимно однозначное отображение j: V1 ® V2, сохраняющее смежность.
Определение. Маршрутом (путем) для графа G(V, X) называется последовательность v1x1v2x2v3…xkvk+1. Маршрут называется замкнутым, если его начальная и конечная точки совпадают. Число ребер (дуг) маршрута (пути) графа называется длиной маршрута (пути).
Определение. Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.
Определение. Замкнутый маршрут (путь) называется циклом (контуром). Цикл, в котором все вершины попарно различны, называется простым циклом.
Матрицы графов.
Пусть D = (V, X) – орграф, где V = {v1, …, vn}, X = {x1, … , xm}.
Определение. Матрицей смежности орграфа D называется квадратичная матрица A(D) = [aij] порядка п, у которой
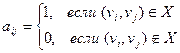
Определение. Если вершина v является концом ребра х, то говорят, что v и х – инциндентны.
Определение. Матрицей инциндентности оргафа D называется матрица размерности п´т B(D) = [bij], у которой
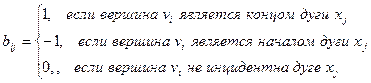
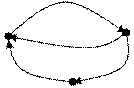
Пример. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.
x1
v1 x4 v2
x2
x3
v3
Составим матрицу смежности:
| v1 | v2 | v3 | |
| v1 | 0 | 1 | 0 |
| v2 | 1 | 0 | 1 |
| v3 | 1 | 0 | 0 |
Т.е. 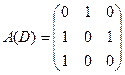 - матрица смежности.
- матрица смежности.
Матрица инциндентности:
| x1 | x2 | x3 | x4 | |
| v1 | -1 | 0 | 1 | 1 |
| v2 | 1 | -1 | 0 | -1 |
| v3 | 0 | 1 | -1 | 0 |
Т.е. 
Если граф имеет кратные дуги (ребра), то в матрице смежности принимается aij= k, где k – кратность дуги (ребра).
С помощью матриц смежности и инциндентности всегда можно полностью определить граф и все его компоненты. Такой метод задания графов очень удобен для обработки данных на ЭВМ.
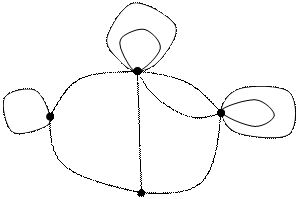
Пример. Задана симметрическая матрица Q неотрицательных чисел. Нарисовать на плоскости граф G(V, X), имеющий заданную матицу Q своей матрицей смежности. Найти матрицу инциндентности R графа G. Нарисовать также орграф 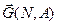 , имеющий матрицу смежности Q, определить его матрицу инциндентности С.
, имеющий матрицу смежности Q, определить его матрицу инциндентности С.
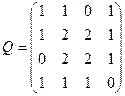
 x4
x4
x3
v2
x2 x5
x6
x1 v1 v3 x7 x8
x10
x11 x9
v4
Составим матрицу инциндентности:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | |
| v1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| v2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| v3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| v4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Итого: 
Построим теперь ориентированный граф с заданной матрицей смежности.





 x4
x4
x5
 |

 v2
v2

 x2 x7
x2 x7

 х3 x6
х3 x6

 x1 v1 х8 v3 x10 x11
x1 v1 х8 v3 x10 x11
х9
х17 х15 x14
x16 х13 x12
v4
Составим матрицу инциндентности для ориетированного графа.
Элемент матрицы равен 1, если точка является концом дуги, -1 – если началом дуги, если дуга является петлей, элемент матрицы запишем как ±1.
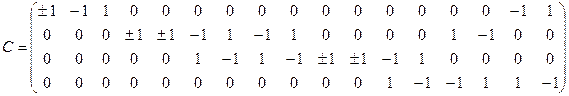
Таким образом, операции с графами можно свести к операциям с их матрицами.
Задание
Вариант 1.
Задача1.Ориентированный граф 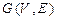 с множеством вершин
с множеством вершин 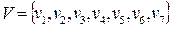 задан списком дуг
задан списком дуг 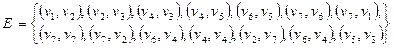 .
.
Построить реализацию графа 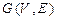 . Построить матрицу смежности и матрицу инцидентности графа
. Построить матрицу смежности и матрицу инцидентности графа 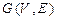 . Укажите степени вершин графа.
. Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 9 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 2.
Задача1.Ориентированный граф 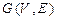 с множеством вершин
с множеством вершин 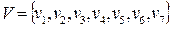 задан списком дуг
задан списком дуг 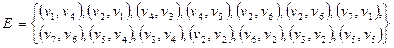 .
.
Построить реализацию графа 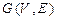 . Построить матрицу смежности и матрицу инцидентности графа
. Построить матрицу смежности и матрицу инцидентности графа 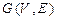 . Укажите степени вершин графа.
. Укажите степени вершин графа.
Задача2. Решите задачу, решение представьте в виде графа: из 27 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 3.
Задача1.Ориентированный граф 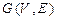 с множеством вершин
с множеством вершин 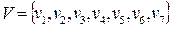 задан списком дуг
задан списком дуг 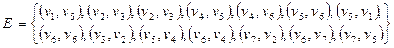 .
.
Построить реализацию графа 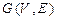 . Построить матрицу смежности и матрицу инцидентности графа
. Построить матрицу смежности и матрицу инцидентности графа 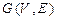 . Укажите степени вершин графа.
. Укажите степени вершин графа.
Задача 3. Решите задачу, решение представьте в виде графа: из 18 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 4.
Задача1.Ориентированный граф 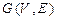 с множеством вершин
с множеством вершин 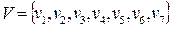 задан списком дуг
задан списком дуг 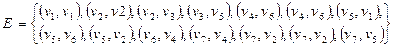 .
.
Построить реализацию графа 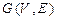 . Построить матрицу смежности и матрицу инцидентности графа
. Построить матрицу смежности и матрицу инцидентности графа 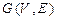 . Укажите степени вершин графа.
. Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 12 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 5.
Задача1.Ориентированный граф 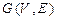 с множеством вершин
с множеством вершин 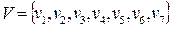 задан списком дуг
задан списком дуг 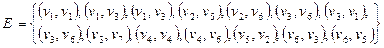 .
.
Построить реализацию графа 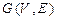 . Построить матрицу смежности и матрицу инцидентности графа
. Построить матрицу смежности и матрицу инцидентности графа 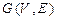 . Укажите степени вершин графа.
. Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 15 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 6.
Задача1.Ориентированный граф 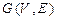 с множеством вершин
с множеством вершин 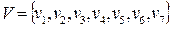 задан списком дуг
задан списком дуг 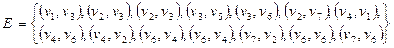 .
.
Построить реализацию графа 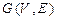 . Построить матрицу смежности и матрицу инцидентности графа
. Построить матрицу смежности и матрицу инцидентности графа 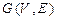 . Укажите степени вершин графа.
. Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 21 монеты одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Графы являются «топологическими» или «геометрическими» объектом.
2. Каково соотношение между количествами вершин, рёбер и граней в плоском графе.
3. Приведите простейшие примеры неплоских графов.
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 4
Пояснения к работе
Комбинаторика
| - раздел математики, изучающий количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества. | |
|
| |
| Правило суммы Если объект А можно выбрать m способами, а объект В – k способами (не такими как А), то выбрать либо А, либо В можно m + k способами. | Правило произведения Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора А) k способами, то пары объектов А и В можно выбрать mk способами. |
|
| |
| Конечное множество различных элементов – генеральная совокупность без повторений. | |
|
| |
| Произвольная группа элементов данной генеральной совокупности – выборка без повторений. | |
| Виды выборок |
Размещения– выборки,
составленные из n различных элементов генеральной совокупности по m элементов, которые отличаются либо составом элементов, либо их порядком.
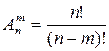
| Перестановки-выборки,
составленные из одних и
тех же n элементов
генеральной совокупности
и отличающиеся
только порядком
их расположения.
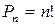
| Сочетания – выборки, составленные из n
различных элементов
генеральной совокупности
по m элементов,
которые отличаются
хотя бы одним элементом.
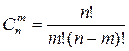
|
| Множество, которое содержит набор n различных классов одинаковых элементов – генеральная совокупность с повторениями. |
| Виды выборок |
Размещения с повторениями – выборки,
составленные из m элементов, выбранных из числа элементов данных n классов генеральной совокупности с повторениями, которые отличаются либо составом элементов, либо их порядком.
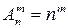
| Размещения с заданным количеством повторений каждого элемента (перестановки) – выборки, которые
отличаются только порядком расположения элементов, когда от i-го класса в каждой выборке участвует 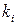 элементов. элементов.
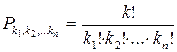 , где , где 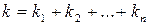
| Сочетания с повторениями – выборки, составленные из m элементов, выбранных из числа элементов данных n классов генеральной совокупности с повторениями,
которые отличаются
хотя бы одним элементом.
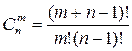
|
Размещения и перестановки – упорядоченные выборки, а сочетания – неупорядоченные выборки.
Символ n! (читается: «эн факториал») есть сокращенное обозначение произведения 1·2·3·…·(n -1)·n.
Принято считать 0! = 1 и 1! = 1.
Примеры.
1. На тренировках занимаются 12 баскетболистов. Сколько может быть образовано тренером разных стартовых пятерок?
Решение. Так как при составлении стартовой пятерки тренера интересует только состав пятерки, то достаточно определить число сочетаний из 12 элементов по 5:
С 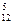 =
= 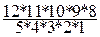 = 792.
= 792.
2. Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг друга?
Решение. Ясно, что в этом случае на каждой горизонтали и каждой вертикали шахматной доски может быть расположено только по одной ладье. Число возможных позиций – число перестановок из 8 элементов:
Р8 = 8! = 8*7*6*5*4*3*2*1 = 40 320.
3. Для полета на Марс необходимо укомплектовать следующий экипаж космического корабля: командир корабля, первый его помощник, второй помощник, два бортинженера и один врач. Командующая тройка может быть отобрана из числа 25 готовящихся к полету летчиков, два борт инженера – из числа20 специалистов, в совершенстве знающих устройство космического корабля, и врач – из числа 8 медиков. Сколькими способами можно укомплектовать экипаж исследователей космоса?
Решение. При выборе командира и его помощников важно определить, какой из военных летчиков лучше других справляется с теми или иными функциями в управлении кораблем. Значит, здесь важен не только персональный состав командующей тройки, но и соответствующая расстановка подобранных людей. Поэтому ясно, что командующая тройка может быть укомплектована А 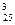 способами.
способами.
Обязанности у обоих бортинженеров примерно одинаковые. Они могут выполнять их по очереди. Следовательно, пара бортинженеров может быть укомплектована С 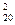 способами. Аналогичное положение и с врачом – его можно подобрать С
способами. Аналогичное положение и с врачом – его можно подобрать С 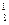 способами.
способами.
В силу правила произведения весь экипаж может быть укомплектован
А 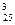 *С
*С 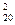 *С
*С 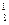 =20976000 способами.
=20976000 способами. 
Задание
Вариант1
1. Профсоюзная организация техникума насчитывает 150 членов. Сколькими способами можно выбрать 6 делегатов на городскую конференцию?
2. Из цифр 1,2,3,4 составлены все возможные двузначные числа, при условии, что: в каждом числе нет одинаковых цифр; цифры в числе могут быть одинаковыми. Сколько получилось чисел?
3. Сколько разных слов можно образовать при перестановке слова «комбинаторика»?
Вариант 2
1. Группа студентов изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть четыре различных урока?
2. Сколькими способами можно выбрать гласную и согласную буквы из слова «полка»?
3. В гастрономе имеются конфеты четырех наименований. Конфеты упакованы в коробки четырех видов – для каждого наименования своя коробка. Сколькими способами можно заказать набор из 6 коробок.
Вариант 3
1. Из цифр 0, 1, 2, 3 составлены все возможные трехзначные числа так, что в каждом числе нет одинаковых цифр; цифры могут быть одинаковые. Сколько получилось чисел?
2. Во взводе 3 сержанта и 30 солдат. Сколькими способами можно выделить одного сержанта и трех солдат для патрулирования?
3. Сколько разных слов можно образовать при перестановке букв слова «соединение»?
Вариант 4
1. Сколько чисел, меньших миллиона, можно записать с помощью цифр 8 и 9?
2. На 5 сотрудников выделено 3 путевки. Сколькими способами их можно распределить, если: все путевки различные; все путевки одинаковые?
3. Для несения почетного караула из 10 человек могут быть приглашены офицеры пехотных войск, авиации, пограничных войск, артиллерии, офицеры морского флота и ракетных войск. Сколькими способами можно избрать состав почетного караула?
Вариант 5
1. Пусть из пункта A в пункт B имеется 5 дорог, а из пункта B в пункт C – 6 дорог. Сколько существует различных вариантов проезда из пункта A в пункт C?
2. В коробке находятся 50 деталей, из которых 10 бракованных. Из коробки наудачу берутся 5 деталей. Найти число различных способов взятия 5-ти деталей, среди которых ровно 3 бракованных.
3. На полке наудачу располагаются 10 книг. Сколько существует различных способов расположения 10-ти книг? Сколько существует различных способов расположения 10-ти книг, при которых 2 заранее помеченные книги окажутся рядом?
Вариант 6
1. Сколько разных четырехзначных чисел можно составить из цифр 0, 1,2,если та же самая цифра может повторяться несколько раз?
2. Сколько можно изготовить трехцветных флажков, если для этого использовать следующие цвета: белый, синий, красный, желтый, зеленый, черный?
3. На студенческий вечер собрались ребята 1, 2, 3 курсов. Вести вечер приглашаются 10 студентов. Сколькими способами можно выбрать ведущих при условии участия в нем хотя бы одного третьекурсника?
Контрольные вопросы.
1. Что изучает комбинаторика?
2. Сформулируйте правило суммы и правило произведения.
3. Чему равен факториал n?
4. Чем отличаются упорядоченные выборки от неупорядоченных выборок?
5. По каким формулам рассчитывают размещения?
6. По каким формулам рассчитывают сочетания?
7. По каким формулам рассчитывают перестановки?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 5
Пояснения к работе
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.
А + В = С ( 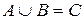 ). ).
| Произведением (или пересечением) нескольких событий называют событие, состоящее в одновременном наступлении всех этих событий в результате испытания.
А·В = С ( 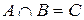 ) )
| Противоположными называют два единственно возможных события, образующих полную группу.
А и 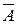 - противоположные события. - противоположные события.
|
Пусть А, В и С – случайные события, выраженные элементарными событиями одного и того же пространства элементарных событий. Тогда следующие события можно записать формулами:
а) событие «произошло только А» записывается формулой 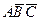 ;
;
б) событие «произошло одно и только одно из данных событий» записывается формулой  +
+ 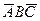 +
+  ;
;
в) событие «произошли два и только два из данных событий» записывается формулой 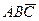 +
+ 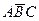 +
+ 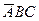 ;
;
г) событие «произошли все три события» записывается формулой 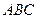 ;
;
д) событие «произошло хотя бы одно из данных событий» записывается формулой А + В + С;
е) событие «произошло не боле двух событий» записывается формулой 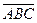 .
.
| Теоремы сложения вероятностей |
Вероятность появления хотя бы одного из двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления. 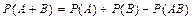
|
Р(АВ) = 0, если события несовместны.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
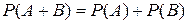
|
Сумма вероятностей противоположных событий равна единице.
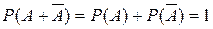
|
Вероятность появления хотя бы одного из событий А1, А2, …, А n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий. 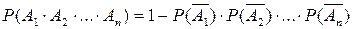
|
| Теоремы умножения вероятностей |
Условной вероятностью события В при условии А называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
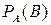 или или 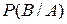
|
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое уже произошло.
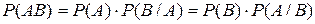
|
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий. 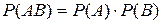 . .
|
| Событие В называют независимым от события А, если появление события А не изменяет вероятности появления события В. |
Пример 1. Вероятность того, что день будет дождливым, р = 0,7. Найти вероятность того, что день будет ясным.
Решение. События «день дождливый» и «день ясный» - противоположные, поэтому искомая вероятность q = 1 – p = 1 – 0,7 =0,3.
Ответ: 0,3.
Пример 2. Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны: 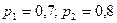 . Найти вероятность попадания при одном залпе (из двух орудий) хотя бы одним из орудий.
. Найти вероятность попадания при одном залпе (из двух орудий) хотя бы одним из орудий.
Решение. Попадание в цель одним из орудий не исключает возможности попадания в цель другим орудием. Значит, события А – «попадание первого орудия» и В – «попадание второго орудия» совместны. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А и В независимы. А поэтому Р(А+В) = Р(А) + Р(В) – Р(А)·Р(В) = 0,7 + 0,8 – 0,7·0,8 = 0,94.
Ответ: 0,94.
Пример 3. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными. 
Решение. Вероятность того, что из первого ящика вынута стандартная деталь (событие А), Р(А) = 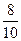 = 0,8. Вероятность того, что из второго ящика вынута стандартная деталь (событие В), Р(В) =
= 0,8. Вероятность того, что из второго ящика вынута стандартная деталь (событие В), Р(В) =  = 0,7. Вероятность того, что из третьего ящика вынута стандартная деталь (событие С), Р(С) =
= 0,7. Вероятность того, что из третьего ящика вынута стандартная деталь (событие С), Р(С) = 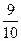 = 0,9. Так как события А, В и С независимы в совокупности, то искомая вероятность (по теореме умножения) равна Р(АВС) = Р(А)Р(В)Р(С) = 0,8∙0,7∙0,9 =0,504.
= 0,9. Так как события А, В и С независимы в совокупности, то искомая вероятность (по теореме умножения) равна Р(АВС) = Р(А)Р(В)Р(С) = 0,8∙0,7∙0,9 =0,504.
Ответ: 0,504.
Задание
Вариант 1
1. Для сигнализации об аварии установлены 2 независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найдите вероятность того, что при аварии:
а) ни один не сработает;
б) сработает хотя бы один;
в) оба сработают.
2. Вероятность того, что Таня на экзамене получит «5», равна 0,6. Найдите вероятность того, что Таня ответит меньше «5».
Вариант 2
1. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго 0,8. Найдите вероятность того, что при одном залпе в мишень:
а) ни один не попал;
б) хотя бы один попал;
в) оба попали.
2. В экзаменационном билете 3 вопроса. Вероятность того, что студент знает все три вопроса билета, равна 0,4. Найдите вероятность того, что студент знает менее трех вопросов билета.
Вариант 3
1. В двух ящиках находятся детали: в первом – 10 (из них 3 стандартных), во втором – 15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найдите вероятность того, что:
а) обе детали окажутся нестандартными;
б) хотя бы одна деталь стандартная;
в) обе детали стандартные.
2. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенный ему экзаменатором вопрос.
Вариант 4
1. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены два независимых измерения. Найдите вероятность того, что:
а) в двух из них допущена ошибка, превысит заданную точность;
б) хотя бы в одном превысит заданную точность;
в) ни в одном превысит заданную точность.
2. В цехе работают 7 мужчин и три женщины. По табельным номером наудачу отобраны 2 человека. Найти вероятность того, что отобраны мужчина и женщина.
Вариант 5
1. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найдите вероятность того, что из двух проверенных изделий:
а) ни одно не оказалось высшего сорта;
б) хотя бы одно высшего сорта;
в) оба высшего сорта.
2. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что наудачу выбранный билет окажется выигрышным.
Вариант 6
1. Рабочий обслуживает 2 станка, каждый из которых работает независимо один от другого. Вероятность того, что за смену станки не потребуют вмешательства рабочего равны соответственно р1 = 0,3, р2 = 0,2. Найдите вероятность того, что за смену:
а) ни один не потребует вмешательства;
б) хотя бы один станок потребует вмешательства рабочего;
в) оба потребуют вмешательства.
2. В читальном зале имеется шесть учебников по теории вероятности, из которых три в переплете. Библиотекарь берет наудачу учебник. Найдите вероятность того, что он окажется в переплете.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы.
1. Как находить вероятность суммы, произведения событий?
2. Чему равна вероятность достоверного события, невозможного события, случайного события?
3. Какие события называют несовместными, независимыми?
4. Как определяется произведение событий? Какие теоремы умножения вероятностей вы знаете?
5. Как определяются противоположные события? Как вычислить вероятности противоположных событий?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 6
Пояснения к работе
| Случайными называют величины, которые в результате испытания могут принимать одно и только одно возможное значение, заранее неизвестное и зависящее от случайных причин, которые учесть нельзя. Обозначают СВ – Х, Y , Z . |
| Дискретной называют случайную величину, которая может принимать конечное или бесконечное, но счетное, число значений. Закон распределения СВ – это соответствие между возможными значениями СВ и их вероятностями. |
| Способы задания закона распределения СВ |
| Табличный Таблица, первая строка которой содержит возможные значения СВ, а вторая – их вероятности. | Графический
Линия, координаты точек которой соответственно равны значениям СВ и их вероятностям. Для ДСВ – ломаная, отрезки которой соединяют точки с координатами 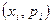 . .
|
Пример. В партии из 8 деталей 5 стандартных. Наудачу взяты 4 детали. Построить ряд распределения числа стандартных деталей среди отобранных, построить многоугольник распределения вероятностей, задать функцию распределения, построить ее график.
Решение.
| Х | 1 | 2 | 3 | 4 |
| Р | 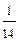
| 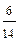
| 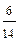
| 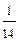
|
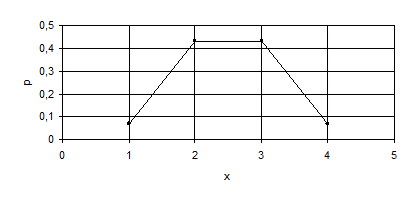
Математическим ожиданием М(х) ДСВХ называют сумму произведений всех ее возможных значений
на их вероятности: 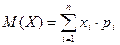 .
Вероятностный смысл математического ожидания - математическое ожидание – центр распределения. .
Вероятностный смысл математического ожидания - математическое ожидание – центр распределения.
|
Дисперсией 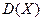 ДСВХ называют математическое ожидание квадрата отклонения СВ от ее математического ожидания М(х) ДСВХ называют математическое ожидание квадрата отклонения СВ от ее математического ожидания М(х) 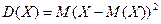 .
Вероятностный смысл дисперсии: дисперсия СВ – характеристика отклонения (рассеяния) значений данной величины от центра. .
Вероятностный смысл дисперсии: дисперсия СВ – характеристика отклонения (рассеяния) значений данной величины от центра.
|
Средним квадратическим отклонением 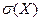 СВХ называют квадратный корень из ее дисперсии СВХ называют квадратный корень из ее дисперсии
 .
Среднее квадратическое отклонение СВ – характеристика рассеяния значений данной величины от центра. .
Среднее квадратическое отклонение СВ – характеристика рассеяния значений данной величины от центра.
|
Пример. ДСВХ задана законом распределения:
Х 2 3 5
Р 0,1 0,4 0,5
Найти математическое ожидание случайной величины Х.
Решение. М(Х) =2∙0,1 + 3∙0,4 + 5∙0,5 = 3,9.
Ответ: 3,9.
Пример. Найти дисперсию и среднее квадратическое отклонение ДСВ Х, которая задана законом распределения:
Х 2 3 5
Р 0,1 0,6 0,3
Решение. М(Х) = 2∙0,1 + 3∙0,6 + 5∙0,3 = 3,5. М(Х2) = 4∙0,1 + 9∙0,6 + 25∙0,3 = 13,3. D ( X ) = 13,3 – (3,5)2 = 1,05. 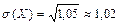 Ответ: 1,05; 1,02.
Ответ: 1,05; 1,02.
Задание
Вариант 1
1. ДСВ задана законом распределения
Х 6 3 1
Р 0,2 0,3 0,5.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Вероятность отказа детали за время испытания на надежность равна 0,3. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 3 деталей.
Вариант 2
1. ДСВ задана законом распределения
Х 2 3 5
Р 0,1 0,4 0,5.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 3 деталей.
Вариант 3
1. ДСВ задана законом распределения
Х 1 2 4
Р 0,1 0,3 0,6.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Вероятность отказа детали за время испытания на надежность равна 0,1. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 4 деталей.
Вариант 4
1. ДСВ задана законом распределения
Х 2 4 8
Р 0,1 0,5 0,4.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. Вероятность отказа детали за время испытания на надежность равна 0,1. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 4 деталей.
Вариант 5.
1. ДСВ задана законом распределения
Х 2 10 20 30
Р 0,2 0,3 0,3 0,2 .
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
1. В партии из 6 деталей имеется 3 окрашеных. Наудачу отобраны 3 детали. Найти числовые характеристики дискретной случайной величины Х – числа окрашенных деталей среди отобранных.
Вариант 6.
1. ДСВ задана законом распределения
Х 2 4 8 10
Р 0,1 0,3 0,4 0,2.
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2. 2. В партии из 10 деталей содержится 3 нестандартных. Наудачу отобраны 2 детали. Найти числовые характеристики дискретной случайной величины
Х – числа нестандартных деталей среди отобранных.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Как вычисляют математическое ожидание случайной величины?
2. В чем заключается вероятностный смысл математического ожидания?
3. Как вычисляют дисперсию случайной величины?
4. В чем заключается вероятностный смысл дисперсии?
5. Как вычисляют среднее квадратическое отклонение случайной величины?
6. В чем заключается вероятностный смысл среднего квадратического отклонения?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 7
Пояснения к работе
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 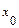 , кроме, быть может, самой точки
, кроме, быть может, самой точки  . Число А называется пределом функции ƒ(x) при
. Число А называется пределом функции ƒ(x) при 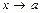 , если для любого сколь угодно малого ε > 0 найдется такое δ > 0, что
, если для любого сколь угодно малого ε > 0 найдется такое δ > 0, что  при
при 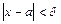 . Запись
. Запись 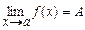 .
.
Если предел функции 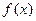 в точке
в точке 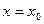 существует, то он единственный.
существует, то он единственный.
Аналогично, 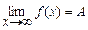 , если
, если  при
при 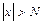 .
.
Функцию 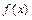 называют бесконечно большой при
называют бесконечно большой при 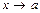 , если
, если  .
.
Функцию называют бесконечно малой при 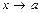 , если
, если 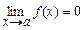 .
.
Если функция ƒ(x) – бесконечно малая, то функция 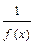 есть бесконечно большая функция и наоборот: если функция ƒ(x) – бесконечно большая, то
есть бесконечно большая функция и наоборот: если функция ƒ(x) – бесконечно большая, то 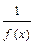 - бесконечно малая.
- бесконечно малая.
Теоремы о пределах.
Теорема 1. Пусть  существуют, тогда
существуют, тогда 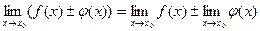 ;
;
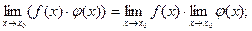

 ;
;  .
.
Теорема 2. Предел многочлена 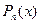 в точке
в точке 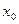 равен значению этого многочлена в точке
равен значению этого многочлена в точке 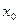 , т. е.
, т. е. 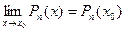 .
.
Вычислить пределы:
1.  .
.
2. 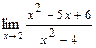 . Здесь пределы числителя и знаменателя равны 0, т. е. мы получили неопределенность
. Здесь пределы числителя и знаменателя равны 0, т. е. мы получили неопределенность  . Разложим на множители числитель и знаменатель дроби. Числитель разложим на множители по формуле
. Разложим на множители числитель и знаменатель дроби. Числитель разложим на множители по формуле  , где
, где 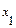 и
и 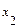 корни уравнения
корни уравнения 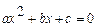 . Знаменатель разложим на множители по формуле
. Знаменатель разложим на множители по формуле 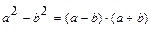 .
.  .
.
3. 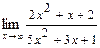 . При
. При  числитель и знаменатель дроби – бесконечно большие функции, т. е. дана неопределенность
числитель и знаменатель дроби – бесконечно большие функции, т. е. дана неопределенность 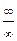 . Раскрывают такую неопределенность делением числителя и знаменателя дроби на наибольшую степень переменной знаменателя, в данном случае на
. Раскрывают такую неопределенность делением числителя и знаменателя дроби на наибольшую степень переменной знаменателя, в данном случае на 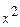 .
.  .
.
Замечательные пределы позволяют раскрыть неопределенности  и
и  .
.
Первый замечательный предел: 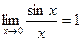 или
или 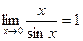 .
.
Второй замечательный предел: 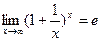 или
или 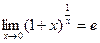 .
.
Вычислить пределы функций:
1. 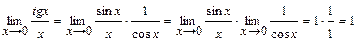 .
.
2. 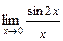 . Решение. Обозначим
. Решение. Обозначим 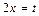 , тогда
, тогда 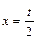 . Если
. Если 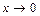 , то
, то 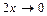 , а значит
, а значит 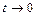 .
.
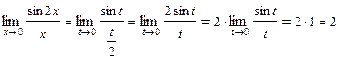 .
.
3. 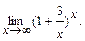 Решение. Сделаем замену переменной, полагая
Решение. Сделаем замену переменной, полагая 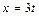 , тогда при
, тогда при  и
и 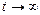 . Следовательно,
. Следовательно,  .
.
4. 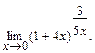 Решение. Обозначим
Решение. Обозначим 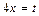 , тогда
, тогда 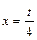 . Если
. Если 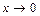 , то
, то 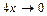 , а значит
, а значит 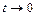 .
.
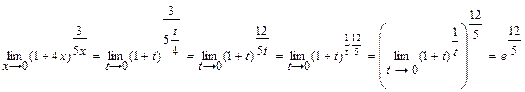 .
.
Здесь использовали свойство предела. «Пусть дана функция ƒ(φ(х)), причем функция ƒ - непрерывная на множестве значений функции у = φ(х), тогда 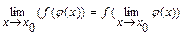 ».
».
Задание.
Вариант 1.
Задача 1. Найдите пределы функций: а) 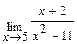 ; б)
; б) 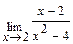 ; в)
; в) 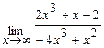 .
.
Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 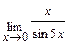 ;
;
б) 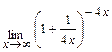 .
.
Вариант 2.
Задача 1. Найдите пределы функций: а) 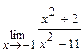 ; б)
; б)  ; в)
; в) 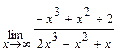 .
.
Задача 2. Примените замечательные пределы для нахождения пределов функций: а)  ; б)
; б) 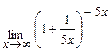 .
.
Вариант 3.
Задача 1. Найдите пределы функций: а) 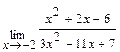 ; б)
; б) 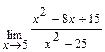 ; в)
; в)  .
.
Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 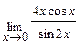 ; б)
; б) 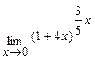 .
.
Вариант 4.
Задача 1. Найдите пределы функций: а) 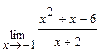 ; б)
; б) 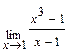 ; в)
; в) 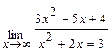 .
.
Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 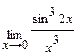 ; б)
; б) 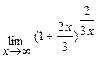 .
.
Вариант 5.
Задача 1. Найдите пределы функций: а)  ; б)
; б) 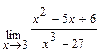 ; в)
; в)  .
.
Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 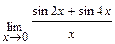 ; б )
; б ) 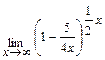 .
.
Вариант 6.
Задача 1. Найдите пределы функций: а)  ; б)
; б) 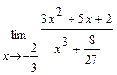 ; в)
; в) 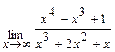 .
.
Задача 2. Примените замечательные пределы для нахождения пределов функций: а) 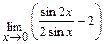 ; б)
; б)  .
.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Какая существует связь между бесконечно большой и бесконечно малой функциями?
2. Как раскрывают неопределенности 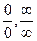 ?
?
3. Какими теоремами о пределах вы пользовались при вычислении пределов?
4. Какие неопределенности помогают раскрыть замечательные пределы?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 8
Пояснения к работе
Производной функции 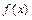 в точке
в точке 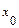 называется предел отношения приращения
называется предел отношения приращения 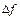 к приращению аргумента
к приращению аргумента 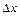 , когда приращение аргумента стремится к нулю:
, когда приращение аргумента стремится к нулю: 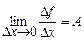 .
.
Функция 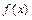 , имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
Основные правила дифференцирования:
Пусть U=U(x) и V=V(x) – функции, имеющие производные.
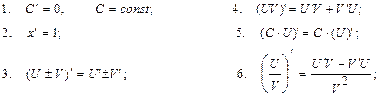
Формулы дифференцирования:
1. 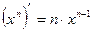 ; 2.
; 2. 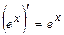 ; 3.
; 3. 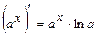 ; 4.
; 4. 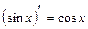 ; 5.
; 5. 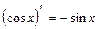 ; 6.
; 6. 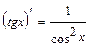 ;7.
;7. 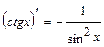 ; 8.
; 8. 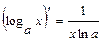 ; 9.
; 9. 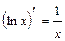 ; 10.
; 10. 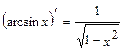 ; 11.
; 11. 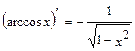 ; 12.
; 12. 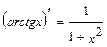 ; 13.
; 13. 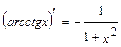 ; 14.
; 14.  .
.
Производная сложной функции: 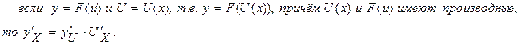
Пример 1. Найти производные функций: 1) 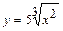 , 2)
, 2) 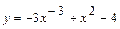 , 3)
, 3)  , 4)
, 4) 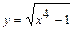 , 6)
, 6) 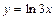 , 7)
, 7) 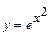 , 8)
, 8) 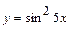 .
.
Решение. 1) 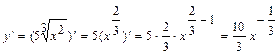 . При вычислении производной перешли от корня к степени с рациональным показателем
. При вычислении производной перешли от корня к степени с рациональным показателем 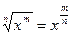 , затем использовали правилом 5 и 1 формулой дифференцирования.
, затем использовали правилом 5 и 1 формулой дифференцирования.
2)  . При вычислении производной пользовались правилами 1, 3, 5 и 1 формулой дифференцирования.
. При вычислении производной пользовались правилами 1, 3, 5 и 1 формулой дифференцирования.
3)  . При вычислении производной пользовались правилом вычисления производной сложной функции и правилами 1, 3, 5, а также 1 формулой дифференцирования.
. При вычислении производной пользовались правилом вычисления производной сложной функции и правилами 1, 3, 5, а также 1 формулой дифференцирования.
4) 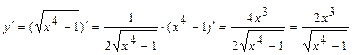 . При вычислении производной пользовались правилом вычисления производной сложной функции и правилами 1, 3, а также формулами дифференцирования 1 и 14.
. При вычислении производной пользовались правилом вычисления производной сложной функции и правилами 1, 3, а также формулами дифференцирования 1 и 14.
5) 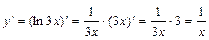 . При вычислении производной пользовались правилом вычисления производной сложной функции и правилом 3 и 9 формулой дифференцирования.
. При вычислении производной пользовались правилом вычисления производной сложной функции и правилом 3 и 9 формулой дифференцирования.
6) 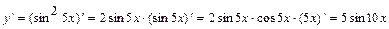 . При вычислении производной пользовались правилом вычисления производной сложной функции, 4 и 1 формулами дифференцирования. При упрощении результата пользовались формулой двойного аргумента
. При вычислении производной пользовались правилом вычисления производной сложной функции, 4 и 1 формулами дифференцирования. При упрощении результата пользовались формулой двойного аргумента 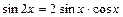 .
.
Задание
Вариант 1
Задача 1. Найдите производные функций: а) 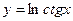 ; б)
; б) 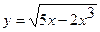 .
.
Задача 2. Вычислите значение производных заданных функций в указанных точках: а) 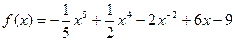 ,
,  ; б)
; б) 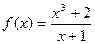 ,
, 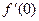 ; в)
; в) 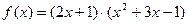 ,
, 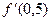 ;
;
Вариант 2
Задача 1. Найдите производные функций: а) 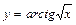 ; б)
; б) 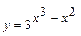 .
.
Задача 2. Вычислите значение производных заданных функций в указанных точках: а) 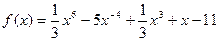 ,
,  ; б)
; б) 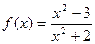 ,
, 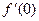 ; в)
; в) 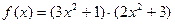 ,
, 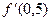 .
.
Вариант 3
Задача 1. Найдите производные функций: а) 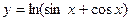 ; б)
; б) 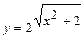 .
.
Задача 2. Вычислите значение производных заданных функций в указанных точках: а) 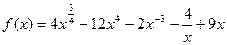 ,
, 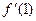 ; б)
; б)  ,
, 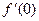 ; в)
; в) 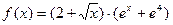 ,
, 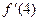 .
.
Вариант 4
Задача 1. Найдите производные функций: а) 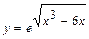 ; б)
; б) 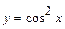 .
.
Задача 2. Вычислите значение производных заданных функций в указанных точках: а) 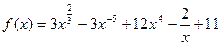 ,
, 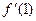 ; б)
; б) 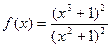 ,
, 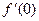 ; в)
; в) 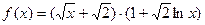 ,
,  .
.
Вариант 5
Задача 1. Найдите производные функций: а) 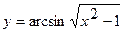 ; б)
; б) 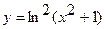 .
.
Задача 2. Вычислите значение производных заданных функций в указанных точках: а) 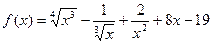 ,
, 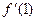 ; б)
; б) 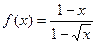 ,
, 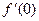 ; в)
; в) 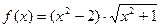 ,
,  .
.
Вариант 6
Задача 1. Найдите производные функций: а) 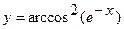 ; б)
; б) 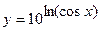 .
.
Задача 2. Вычислите значение производных заданных функций в указанных точках: а) 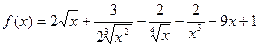 ,
, 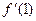 ; б)
; б) 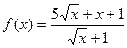 ,
, 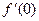 ; в)
; в) 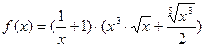 ,
, 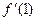 .
.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Как вычисляют производную сложной функции?
2. Какими правилами дифференцирования вы пользовались при нахождении производных функций?
3. Какими формулами дифференцирования вы пользовались при нахождении производных функций?
4. Как называют операцию нахождения производной функции?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 9
Пояснения к работе
Задание
Вариант 1
Задача. Исследовать функцию  на монотонность и экстремумы, построить график.
на монотонность и экстремумы, построить график.
Вариант 2
Задача. Исследовать функцию 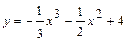 на монотонность и экстремумы, построить график.
на монотонность и экстремумы, построить график.
Вариант 3
Задача. Исследовать функцию 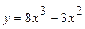 на монотонность и экстремумы, построить график.
на монотонность и экстремумы, построить график.
Вариант 4
Задача. Исследовать функцию 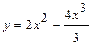 на монотонность и экстремумы, построить график
на монотонность и экстремумы, построить график
Вариант 5
Задача. Исследовать функцию 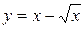 на монотонность и экстремумы, построить график.
на монотонность и экстремумы, построить график.
Вариант 6
Задача. К источнику постоянного тока с электродвижущейся силой Е и внутренним сопротивлением 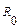 подключено внешнее сопротивление
подключено внешнее сопротивление 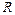 . При каком
. При каком  мощность, выделяемая во внешней цепи, будет максимальной, если
мощность, выделяемая во внешней цепи, будет максимальной, если 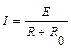 и
и 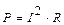 ? Построить график мощности.
? Построить график мощности.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Что можно сказать о движении, если тело движется прямолинейно по закону S=S(t) и а) S’(t)=1; б)S’(t)=2t?
2. В чём заключается физический и геометрический смысл производной?
3. Как выяснить монотонность функции?
4. Как найти экстремумы функции?
5. Как связана сила тока с величиной заряда, протекающего по проводнику?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 10
Пояснения к работе
Неопределенный интеграл
Функция 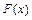 называется первообразной для функции
называется первообразной для функции 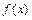 в промежутке
в промежутке 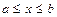 , если в любой точке этого промежутка её производная равна
, если в любой точке этого промежутка её производная равна 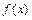 :
: 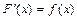 .
.
Отыскание первообразной функции по заданной её производной есть действие, обратное дифференцированию, - интегрирование.
Совокупность первообразных для функции 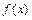 называют неопределенным интегралом и обозначают символом
называют неопределенным интегралом и обозначают символом 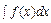 . Таким образом,
. Таким образом, 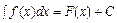 . Здесь
. Здесь 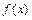 - подынтегральная функция;
- подынтегральная функция;  - подынтегральное выражение; С – произвольная постоянная.
- подынтегральное выражение; С – произвольная постоянная.
Основные свойства неопределенного интеграла:
1. 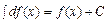 .
.
2. 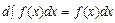 ;
; 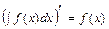 .
.
3. 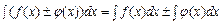 .
.
4.  .
.
Замена переменной.
Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла 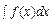 в интеграл
в интеграл 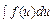 , который легко вычисляется по какой-либо из основных формул интегрирования. Формула замены переменной имеет вид
, который легко вычисляется по какой-либо из основных формул интегрирования. Формула замены переменной имеет вид  где
где 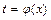 .
.
Найти следующие интегралы.
1) 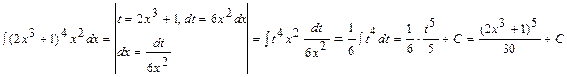 .
.
2) 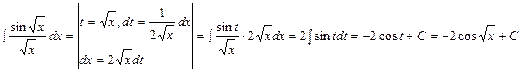 .
.
В практике интегрирования часто встречаются интегралы, для нахождения которых можно, не производя подробного решения методом подстановки, использовать формулу 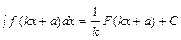 . Например,
. Например, 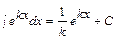 ,
, 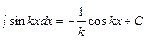 ,
, 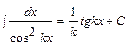 .
.
Определенный интеграл.
Пусть функция 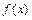 определена на отрезке
определена на отрезке 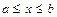 . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками  . Выберем на каждом элементарном отрезке
. Выберем на каждом элементарном отрезке 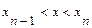 произвольную точку
произвольную точку 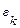 , и вычислим значение функции в точках
, и вычислим значение функции в точках 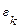 –
– 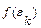 . Обозначим длину каждого элементарного отрезка
. Обозначим длину каждого элементарного отрезка  через
через 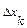 . Интегральной суммой для функции
. Интегральной суммой для функции 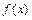 на отрезке
на отрезке 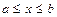 называют сумму вида
называют сумму вида 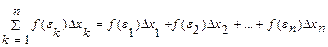 .
.
Определенным интегралом от функции f( x) на отрезке [a; в] называют предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю
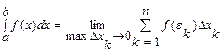 .
.
Если функция f( x) непрерывна на [a; b], то предел интегральной суммы всегда существует и не зависит от способа разбиения отрезка [a; b] на элементарные отрезки и от выбора точек 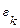 .
.
Для вычисления определенного интеграла от функции 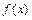 в том случае, когда можно найти соответствую первообразную данной функции
в том случае, когда можно найти соответствую первообразную данной функции 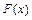 , служит формула Ньютона - Лейбница
, служит формула Ньютона - Лейбница 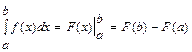 , т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
, т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Задание.
Вариант 1
Задача. Вычислите следующие определенные интегралы: а)  ; б)
; б) 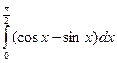 ;
;
в) 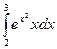 .
.
Вариант 2
Задача. Вычислите следующие определенные интегралы:
а) 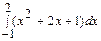 ; б)
; б) 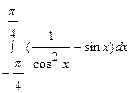 ; в)
; в) 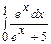 .
.
Вариант 3
Задача. Вычислите следующие определенные интегралы:
а)  ; б)
; б) 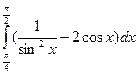 ; в)
; в) 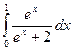 .
.
Вариант 4
Задача. Вычислите следующие определенные интегралы:
а) 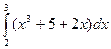 ; б)
; б) 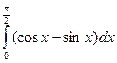 ; в)
; в) 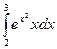 .
.
Вариант 5
Задача. Вычислите следующие определенные интегралы:
а) 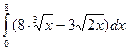 ; б)
; б) 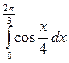 ; в)
; в) 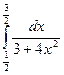 .
.
Вариант 6
Задача. Вычислите следующие определенные интегралы:
а) 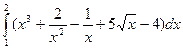 ; б)
; б) 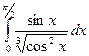 ; в)
; в) 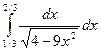 .
.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Какие методы интегрирования вы применяли при вычислении интегралов?
2. Какими формулами интегрирования вы пользовались при вычислении интегралов?
3. Как называют операцию нахождения первообразной функции?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 11
Пояснения к работе
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
6. Как вычислить площадь плоской фигуры?
7. Как по известной скорости находить пройденный путь?
8. Как находить закон движения точки, если известна скорость или ускорение?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 12
Пояснения к работе
Дифференциальным уравнением с разделяющимися переменными называют дифференциальное уравнение первого порядка вида  .
.
Если перейти к дифференциалам ( 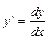 ), то это уравнение примет вид
), то это уравнение примет вид 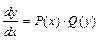 . Умножив обе части уравнения на dx, получим уравнение
. Умножив обе части уравнения на dx, получим уравнение 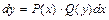 . Если разделить последнее уравнение на
. Если разделить последнее уравнение на 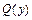 , то получим уравнение с разделенными переменными
, то получим уравнение с разделенными переменными 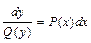 , проинтегрировав которое получим общий интеграл
, проинтегрировав которое получим общий интеграл 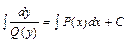 .
.
Найти общее решение дифференциального уравнения 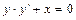
Решение: перейдем в данном уравнении к дифференциалам 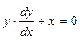 . Перенесем слагаемое х в правую часть уравнения
. Перенесем слагаемое х в правую часть уравнения 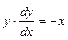 . Умножим обе части уравнения на dx, получим уравнение с разделенными переменными
. Умножим обе части уравнения на dx, получим уравнение с разделенными переменными 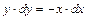 . Проинтегрируем обе части уравнения
. Проинтегрируем обе части уравнения 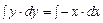 . Найдем интегралы:
. Найдем интегралы: 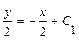 . Если обозначить
. Если обозначить  , то получим уравнение
, то получим уравнение 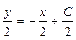 . Умножив обе части на 2, получим общее решение
. Умножив обе части на 2, получим общее решение 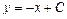 . Ответ:
. Ответ: 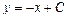 .
.
Однородным дифференциальным уравнением первого порядка называют дифференциальное уравнение (ДУ) вида 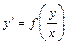 .
.
Это уравнение приводят к уравнению с разделяющимися переменными относительно новой функции, выполнив следующую замену 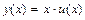 или
или 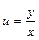 . Тогда
. Тогда 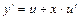 и, после подстановки в исходное уравнение полученных выражений, уравнение примет вид
и, после подстановки в исходное уравнение полученных выражений, уравнение примет вид 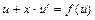 . Это уравнение с разделяющимися переменными, разделим переменные
. Это уравнение с разделяющимися переменными, разделим переменные 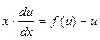 ;
; 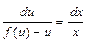 . Интегрируя, получим общий интеграл относительно переменных
. Интегрируя, получим общий интеграл относительно переменных 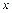 и
и 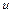 . Затем необходимо вернуться к прежним переменным.
. Затем необходимо вернуться к прежним переменным.
Например, найти общее решение ДУ: 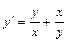 . Обозначим
. Обозначим 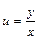 или
или 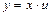 . Тогда
. Тогда 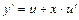 и уравнение примет вид
и уравнение примет вид  ;
; 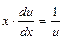 ;
;  . Интегрируя, получим
. Интегрируя, получим  ;
; 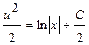 ;
; 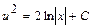 . Вернёмся к прежним переменным
. Вернёмся к прежним переменным 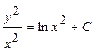 . Ответ:
. Ответ: 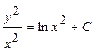 .
.
Задание
Вариант 1
Задача 1. Найдите общее решение дифференциального уравнения: 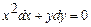 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 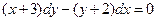 , если y = 3 при x = 2.
, если y = 3 при x = 2.
Вариант 2
Задача 1. Найдите общее решение дифференциального уравнения: 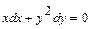 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 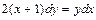 , если y = 2 при х =1.
, если y = 2 при х =1.
Вариант 3
Задача 1. Найдите общее решение дифференциального уравнения:  .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 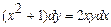 , если y = 2 при х = 1.
, если y = 2 при х = 1.
Вариант 4
Задача 1. Найдите общее решение дифференциального уравнения: 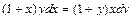 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 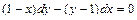 , если y = 3 при x = 2.
, если y = 3 при x = 2.
Вариант 5
Задача 1. Найдите общее решение дифференциального уравнения: 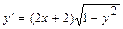 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 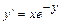 , если y = 0 при x = 1.
, если y = 0 при x = 1.
Вариант 6
Задача 1. Найдите общее решение дифференциального уравнения: 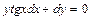 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 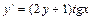 , если y = 0 при x = 0.
, если y = 0 при x = 0.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Каков алгоритм решения дифференциальных уравнений с разделяющимися переменными?
2. Что является решением дифференциального решения?
3. Как находят частное решение дифференциального уравнения с разделяющимися переменными и однородного дифференциального уравнения первого порядка?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 13
Пояснения к работе
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называют уравнение вида 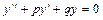 или
или 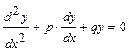 , где p и q – постоянные величины.
, где p и q – постоянные величины.
Для отыскания общего решения данного уравнения составляют характеристическое уравнение 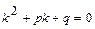 , которое получается из данного уравнения заменой
, которое получается из данного уравнения заменой 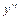 ,
, 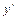 и
и 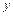 на соответствующую степень переменной
на соответствующую степень переменной  , причем сама функция
, причем сама функция 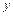 заменяется единицей.
заменяется единицей.
Общее решение данного уравнения строится в зависимости от корней характеристического уравнения. Возможны три случая:
1). Дискриминант уравнения 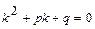 положительный, т. е. характеристическое уравнение имеет два различных действительных корня
положительный, т. е. характеристическое уравнение имеет два различных действительных корня 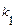 и
и 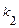 . В этом случае общее решение уравнения имеет вид
. В этом случае общее решение уравнения имеет вид 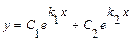
2). Дискриминант уравнения 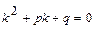 равен нулю, т. е. характеристическое уравнение имеет два равных действительных корня
равен нулю, т. е. характеристическое уравнение имеет два равных действительных корня 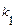 =
= 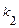 =
= 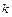 . В этом случае общее решение уравнения имеет вид
. В этом случае общее решение уравнения имеет вид 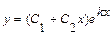 .
.
3). Дискриминант уравнения 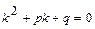 отрицательный, т. е. характеристическое уравнение имеет два комплексно-сопряженных корня
отрицательный, т. е. характеристическое уравнение имеет два комплексно-сопряженных корня 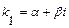 и
и 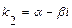 . В этом случае общее решение уравнения имеет вид
. В этом случае общее решение уравнения имеет вид 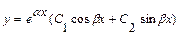 .
.
Найти частное решение уравнения 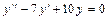 , если
, если 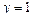 и
и 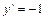 при
при 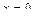 .
.
Решение. Составим характеристическое уравнение и найдем его корни  ,
, 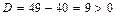 , значит, характеристическое уравнение имеет два различных действительных корня:
, значит, характеристическое уравнение имеет два различных действительных корня: 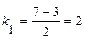 и
и 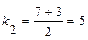 . Общее решение уравнения имеет вид
. Общее решение уравнения имеет вид 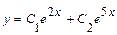 .
.
Для нахождения искомого частного решения нужно определить значения постоянных 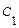 и
и 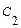 . Найдем производную общего решения
. Найдем производную общего решения 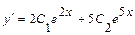 . Подставим начальные условия в общее решение и в его производную, получим систему уравнений:
. Подставим начальные условия в общее решение и в его производную, получим систему уравнений: 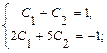
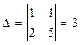 ,
, 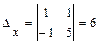 ,
, 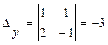 . Значит, по формулам Крамера
. Значит, по формулам Крамера 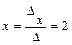 ,
, 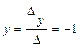 . Следовательно, частное решение имеет вид –
. Следовательно, частное решение имеет вид – 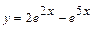 .
.
Задание
Вариант 1
Задача 1. Найдите общее решение дифференциального уравнения: 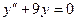 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию:  , если y = 3, y′ = 0 при х = 0.
, если y = 3, y′ = 0 при х = 0.
Вариант 2
Задача 1. Найдите общее решение дифференциального уравнения:  .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 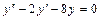 , если y = 4, y′ = 10 при х = 0.
, если y = 4, y′ = 10 при х = 0.
Вариант 3
Задача 1. Найдите общее решение дифференциального уравнения:  .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 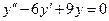 , если y= 1 и y΄= 1 при х = 0.
, если y= 1 и y΄= 1 при х = 0.
Вариант 4
Задача 1. Найдите общее решение дифференциального уравнения: 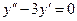 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 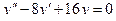 , если y= 2 и y΄= 9 при х = 0.
, если y= 2 и y΄= 9 при х = 0.
Вариант 5
Задача 1. Найдите общее решение дифференциального уравнения: 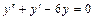 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: 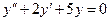 , если y = 1 и y΄= 1 при х = 0.
, если y = 1 и y΄= 1 при х = 0.
Вариант 6
Задача 1. Найдите общее решение дифференциального уравнения: 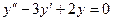 .
.
Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию:  , если y= 1 и y΄= 5 при х = 0.
, если y= 1 и y΄= 5 при х = 0.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Каков алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами?
2. Что является решением дифференциального решения?
3. Как находят частное решение дифференциального уравнения?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 14
Пояснения к работе
Пусть 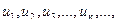 где un= f( n) - бесконечная числовая последовательность.
где un= f( n) - бесконечная числовая последовательность.
Выражение 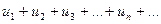 называют бесконечным числовым рядом, а числа
называют бесконечным числовым рядом, а числа 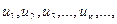 – членами ряда; un= f( n) называется общим членом. Ряды часто записывают в виде
– членами ряда; un= f( n) называется общим членом. Ряды часто записывают в виде 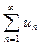 .
.
Сумму первых n членов числового ряда обозначают через 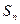 и называют n-ой частичной суммой ряда:
и называют n-ой частичной суммой ряда: 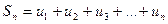 .
.
Ряд называется сходящимся, если его n-я частичная сумма 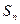 при неограниченном возрастании n стремиться к конечному пределу, т. е. если
при неограниченном возрастании n стремиться к конечному пределу, т. е. если 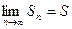 . Число S называют суммой ряда.
. Число S называют суммой ряда.
Если же n-я частичная сумма ряда, при 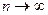 не имеет конечного предела, то ряд называют расходящимся.
не имеет конечного предела, то ряд называют расходящимся.
Ряд 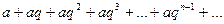 , составленный из членов любой убывающей геометрической прогрессии, называют геометрическим. Он является сходящимся при
, составленный из членов любой убывающей геометрической прогрессии, называют геометрическим. Он является сходящимся при 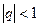 и имеет сумму
и имеет сумму 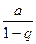 , если же
, если же 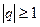 , то геометрический ряд расходится.
, то геометрический ряд расходится.
Ряд 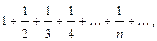 называют гармоническим, он расходится.
называют гармоническим, он расходится.
Задание
Вариант 1
Задача 1. Определите сходимость ряда: а) 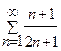 ; б)
; б) 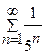 ; в)
; в) 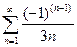 .
.
Задача 2. Найдите радиус и интервал сходимости ряда 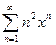 .
.
Вариант 2
Задача 1. Определите сходимость ряда: а) 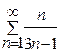 ; б)
; б) 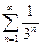 ; в)
; в) 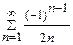 .
.
Задача 2. Найдите радиус и интервал сходимости ряда 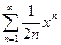 .
.
Вариант 3
Задача 1. Определите сходимость ряда: а)  ; б)
; б) 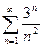 ; в)
; в) 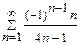 .
.
Задача 2. Найдите радиус и интервал сходимости ряда  .
.
Вариант 4
Задача 1. Определите сходимость ряда: а) 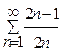 ; б)
; б)  ; в)
; в) 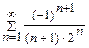 .
.
Задача 2. Найдите радиус и интервал сходимости ряда 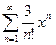 .
.
Вариант 5
Задача 1. Определите сходимость ряда: а) 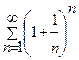 ; б)
; б)  ; в)
; в) 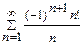 .
.
Задача 2. Найдите радиус и интервал сходимости ряда 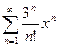 .
.
Вариант 6
Задача 1. Определите сходимость ряда: а) 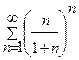 ; б)
; б) 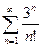 ; в)
; в) 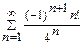 .
.
Задача 2. Найдите радиус и интервал сходимости ряда 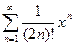 .
.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
Контрольные вопросы.
1. В чем разница между сходящимся рядом и расходящимся?
2. Как применяют необходимый признак сходимости числовых рядов?
3. Как применяют признак Даламбера?
4. Как применяют признак Лейбница?
5. Какой ряд называется условно сходящимся?
6. Как найти радиус сходимости степенного ряда?
7. Какова связь между радиусом сходимости степенного ряда и его интервалом сходимости?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 15
Пояснения к работе
Квадратурные формулы.
Отыскание приближенного значения определенного интеграла на основе значений подынтегральной функции в конечном множестве точек из отрезка интегрирования называют механической квадратурой, а соответствующие приближенные формулы – квадратурными формулами. Используемые при этом аргументы функции называют узлами квадратуры.
Для получения квадратурных формул необходимо:
1) разбить отрезок 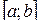 , на котором интегрируют функцию f , разбить на n частей точками
, на котором интегрируют функцию f , разбить на n частей точками
а = х0 < x1 < … < xn = b (  ) – узлы квадратуры. Поскольку способ разбиения может быть любым, то отрезок
) – узлы квадратуры. Поскольку способ разбиения может быть любым, то отрезок 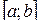 разбиваем на равные части. В этом случае шаг
разбиваем на равные части. В этом случае шаг 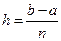 и узлы квадратуры находим по формуле
и узлы квадратуры находим по формуле 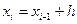 ,
, 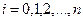 ;
;
2) вычислить значения функции в узлах квадратуры
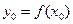 ,
, 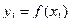 ,
, 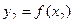 , … ,
, … , 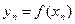 ;
;
3) Воспользоваться квадратурными формулами:
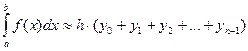 – формула прямоугольников с левыми ординатами;
– формула прямоугольников с левыми ординатами;
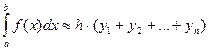 – формула прямоугольников с правыми ординатами;
– формула прямоугольников с правыми ординатами;
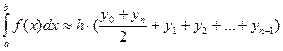 – формула трапеций;
– формула трапеций;
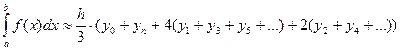 – формула Симпсона.
– формула Симпсона.
Для квадратурной формулы прямоугольников с центральными ординатами необходимо в качестве узлов интерполирования взять середины отрезков разбиения а = х0 < x1 < … < xn = b. Пусть шаг равен 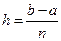 . Значение первого узла квадратуры найдем по формуле
. Значение первого узла квадратуры найдем по формуле 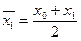 , значения остальных узлов квадратуры найдем по формуле
, значения остальных узлов квадратуры найдем по формуле 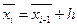 . Вычислим значения функции f(х) в узлах квадратуры
. Вычислим значения функции f(х) в узлах квадратуры 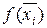 ,
,
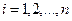 . Формула прямоугольников с центральными ординатами
. Формула прямоугольников с центральными ординатами
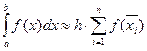 .
.
Задание
Вариант 1
Вычислить интеграл 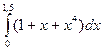 по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 3. Оценить погрешность приближения методом двойного пересчета.
по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 3. Оценить погрешность приближения методом двойного пересчета.
Вариант 2
Вычислить интеграл 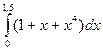 по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 6. Оценить погрешность приближения методом двойного пересчета.
по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 6. Оценить погрешность приближения методом двойного пересчета.
Вариант 3
Вычислить интеграл 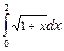 по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 4 . Оценить погрешность приближения методом двойного пересчета.
по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 4 . Оценить погрешность приближения методом двойного пересчета.
Вариант 4
Вычислить интеграл 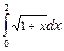 по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 8. Оценить погрешность приближения методом двойного пересчета.
по формулам прямоугольников, формуле трапеций и формуле Симпсона при п = 8. Оценить погрешность приближения методом двойного пересчета.
Вариант 5
Вычислить по формулам прямоугольников, формуле трапеций и формуле Симпсона приближенное значение определенного интеграла 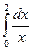 при n = 10 с тремя десятичными знаками.
при n = 10 с тремя десятичными знаками.
Вариант 6
Вычислить по формулам прямоугольников, формуле трапеций и формуле Симпсона приближенное значение определенного интеграла 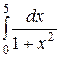 при n = 5 с тремя десятичными знаками.
при n = 5 с тремя десятичными знаками.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Как найти узлы квадратуры?
2. На чем основываются численные методы вычисления определенного интеграла?
3. Как можно получить формулы прямоугольников с левыми, правыми и центральными ординатами?
4. Как можно получить формулу трапеций?
5. Чем отличается формула Симпсона от формулы трапеций?
6. Какая из формул дает лучший результат?
7. В чем суть метода двойного пересчета?
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ ОБУЧАЮЩИХСЯ ПО ПРОВЕДЕНИЮ
ПРАКТИЧЕСКИХ ЗАНЯТИЙ
для специальности
13.02.11 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)»
Учебная дисциплина
«МАТЕМАТИКА»
Смоленск
Г.
Рассмотрено и одобрено
ЦМК общеобразовательных дисциплин
Предс. ЦМК
____________ /Гмырикова С.В./
Протокол №______
«___»___________20__г.
Составитель: Абрамова Г.М., преподаватель ОГБПОУ «Смоленский политехнический техникум»
Рецензент: Филипенко И.В., преподаватель ОГБПОУ «Смоленский политехнический техникум»
Методические указания для обучающихся по проведению практических занятий являются частью основной профессиональной образовательной программы ОГБПОУ «Смоленский политехнический техникум» по специальности 13.02.11 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)» в соответствии с требованиями федеральных государственных образовательных стандартов третьего поколения (далее – ФГОС).
Методические указания для обучающихся по проведению практических занятий включают в себя предисловие, цели работы, пояснения к работе, задание, порядок и образец отчёта, контрольные вопросы, литературу, приложения.
СОДЕРЖАНИЕ
| Номер, название практических занятий | Страницы |
| Практическое занятие №1 «Действия с матрицами» | 5 |
| Практическое занятие №2 «Решение системы линейных уравнений по формулам Крамера » | 8 |
| Практическое занятие №3 «Построение графов. Решение задач c использованием графов.» | 11 |
| Практическое занятие №4 «Решение задач на вычисление размещений, сочетаний, перестановок » | 16 |
| Практическое занятие №5 «Решение простейших задач на определение вероятности с использованием теоремы сложения и умножения вероятностей » | 18 |
| Практическое занятие №6 «Построение распределения дискретной случайной величины по заданному условию.» | 21 |
| Практическое занятие №7 «Вычисление пределов функций различными методами.» | 24 |
| Практическое занятие №8 «Дифференцирование функций. Вычисление производной сложных функций.» | 27 |
| Практическое занятие №9 «Исследование функций с помощью первой и второй производных и построение графиков функций. » | 29 |
| Практическое занятие №10 «Вычисление определенного интеграла » | 32 |
| Практическое занятие №11 «Вычисление площадей фигур, решение задач физического содержания с помощью определённого интеграла.» | 36 |
| Практическое занятие №12 «Решение дифференциальных уравнений с разделяющимися переменными.» | 38 |
| Практическое занятие№13 «Решение линейных однородных уравнений второго порядка с постоянными коэффициентами.» | 39 |
| Практическое занятие №14 «Исследование числовых рядов на сходимость. Определение сходимости рядов по признаку Даламбера.» | 41 |
| Практическое занятие №15 «Численное интегрирование. Формулы прямоугольников, формула Симпсона. Формула трапеций.» | 45 |
ПРЕДИСЛОВИЕ
УВАЖАЕМЫЕ СТУДЕНТЫ!
Методические указания для обучающихся по проведению практических занятий по учебной дисциплине «Математика» созданы вам в помощь для работы на занятиях, правильного составления отчётов. Приступая к выполнению задания, вы должны внимательно прочитать цели, ознакомиться с пояснениями к работе, содержащими краткие теоретические сведения по теме работы и методические рекомендации, ответить на контрольные вопросы.
Практическое занятие содержит задание, состоящее из шести вариантов, включающих задачи, соответствующие указанным в ФГОС требованиям к уровню вашей подготовки. Выполнять задание, делать выводы по проделанной работе вы должны согласно инструкции преподавателя.
Отчёт о работе вы должны оформить по приведённому образцу.
Наличие положительных оценок по практическим занятиям необходимо для допуска к дифференцированному зачету по учебной дисциплине «Математика». В случае отсутствия на учебном занятии по любой причине или получения неудовлетворительной оценки за практическое занятие вы должны выполнить работу или пересдать.
ВНИМАНИЕ! В результате выполнения заданий практических занятий по УД «Математика» вы освоите умения
- решать прикладные задачи в области профессиональной деятельности,
на основе знаний:
– значения математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
- основных математических методов решения прикладных задач в области профессиональной деятельности;
- основных понятий и методов математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
- основ интегрального и дифференциального исчисления.
Желаем вам успехов!
Практическое занятие № 1
Действия с матрицами
Цели: в результате выполнения практической работы, обучающиеся должны уметь выполнять действия с матрицами.
Пояснения к работе
Теоретические сведения:
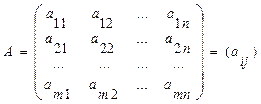 - матрица размера m × n ( i = 1, m, j = 1, n).
- матрица размера m × n ( i = 1, m, j = 1, n).
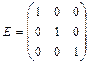 - единичная матрица,
- единичная матрица, 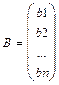 - вектор-столбец,
- вектор-столбец,
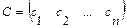 -вектор-строка.
-вектор-строка.
Каждой квадратной матрице (размера n × m) можно поставить в соответствие определённое число, которое называют определителем матрицы.
Ат = 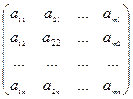 -транспонированная матрица.
-транспонированная матрица.
Матрица А называется невырожденной, если определитель ∆А ≠ 0, в противном случае матрица А называется вырожденной.
А*= 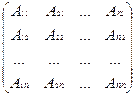 - союзная матрица, А ij – алгебраическое дополнение элемента aij.
- союзная матрица, А ij – алгебраическое дополнение элемента aij.
А-1 называется матрицей обратной матрице А, если выполняется условие
А∙А-1 = А∙А-1 = Е.
Всякая невырожденная матрица имеет себе обратную: А-1= 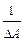 А*.
А*.
Рассмотрим матрицу А m× n.  .
.
Выделим в ней k строк и столбцов k столбцов. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы, обозначают r( A).
Примеры: 1.Найдите значение матричного многочлена 2А2 + 4АВ - 3Е, если Е единичная матрица второго порядка и 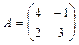 ,
, 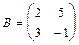 .
.
Решение:
Найдем 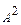 :
: 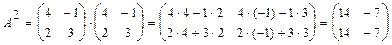 .
.
Умножим 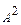 на 2:
на 2:  .
.
Найдем произведение матриц  :
: 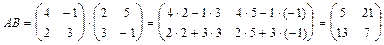 .
.
Найдем значение выражения 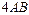 :
: 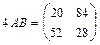 .
.
Найдем произведение единичной матрицы на 3: 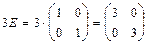 .
.
Найдем значение выражения 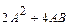 :
: 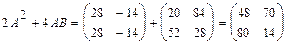 .
.
Найдем значение выражения 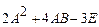 :
: 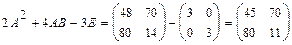 .
.
Ответ: 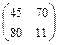 .
.
2. Найти матрицу обратную данной, сделать проверку:
Найти 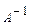 , если
, если 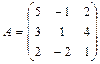 .
.
Решение:
Найдем  :
: 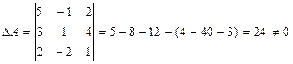 . Матрица невырожденная.
. Матрица невырожденная.
Найдем  :
:
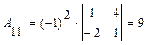 ;
; 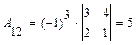 ;
; 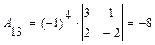 ;
;
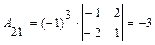 ;
; 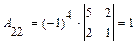 ;
; 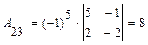 ;
;
 ;
; 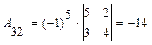 ;
; 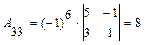 ,
,
поэтому 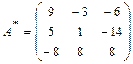 .
.
Найдем 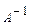 :
: 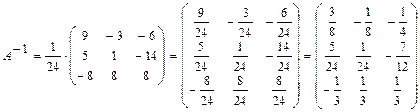 .
.
Проверка: А  .
.
3. Определить ранг матрицы:  .
.
Решение:
Приведем данную матрицу к каноническому виду, для чего выполним три действия: умножим первую строку на -4 и сложим с второй строкой; умножим первую строку на -2 и сложим с третьей строкой; умножим первую строку на 5 и сложим с четвертой строкой.  Выполним два действия: умножим первый столбец на -2 и сложим со вторым, а затем сложим первый и третий столбцы.
Выполним два действия: умножим первый столбец на -2 и сложим со вторым, а затем сложим первый и третий столбцы.  . Поменяем местами вторую и третью строки.
. Поменяем местами вторую и третью строки.  . Умножим второй столбец на -3 и сложим с третьим столбцом.
. Умножим второй столбец на -3 и сложим с третьим столбцом. 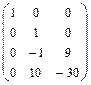 Выполним два действия: сложим вторую и третью строки; умножим вторую строку на -10 и сложим с четвертой строкой.
Выполним два действия: сложим вторую и третью строки; умножим вторую строку на -10 и сложим с четвертой строкой. 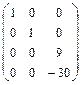 .Разделим 3, 4 строки соответственно на 9, 30.
.Разделим 3, 4 строки соответственно на 9, 30.  . Сложим третью и четвертую строки.
. Сложим третью и четвертую строки. 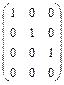 . Значит,
. Значит, 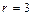 .
.
Задание
Найдите значение матричного многочлена 2А2 + 3В + 5Е, если Е единичная матрица третьего порядка.
1в 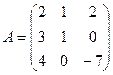 ,
,  . 2в
. 2в 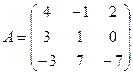 ,
, 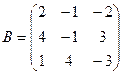 .
.
3в 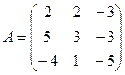 ,
, 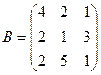 . 4в
. 4в 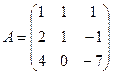 ,
, 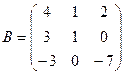 .
.
5в 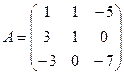 ,
, 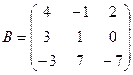 . 6в
. 6в 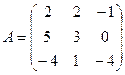 ,
, 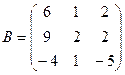 .
.
Содержание отчёта
Отчёт о проделанной работе должен содержать:
- название темы практического занятия;
- цели практического занятия;
- условие задачи;
- подробное решение задачи;
- ответ.
Контрольные вопросы
1. Что называют матрицей? Нулевой матрицей?
2. Какие матрицы называют равными?
3. Какую матрицу называют квадратной? Единичной?
4. Какую матрицу называют вектором?
5. Что является суммой двух матриц? Произведением матрицы на число?
6. Какую матрицу называют противоположной?
7. Сформулировать свойства операций сложения матриц, умножения матрицы на число.
8. Что называют произведением двух матриц? Всегда ли можно найти произведение двух матриц?
9. Сформулировать свойства умножения матриц.
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 2
Дата: 2019-02-19, просмотров: 406.