Нижнекамский химико-технологический институт (филиал)
Федерального государственного бюджетного образовательного учреждения высшего образования
«Казанский национальный исследовательский технологический университет»
Д.В. Елизаров, С.А. Мерзляков
Основы линейных систем управления в автоматизации нефтехимических производств
Учебное пособие
Нижнекамск
2016
Министерство образования и науки Российской Федерации
Нижнекамский химико-технологический институт (филиал)
Федерального государственного бюджетного образовательного учреждения высшего образования
«Казанский национальный исследовательский технологический университет»
Д.В. Елизаров, С.А. Мерзляков
Основы теории управления в автоматизации нефтехимических производств
Учебное пособие
Нижнекамск
2016
УДК
Печатается по решению методического совета Нижнекамского химико-технологического института (филиал) ФГБОУ ВО «КНИТУ»
Рецензенты
Кутузов А.Г., д.т.н., доцент, директор ГБОУ СПО «Нижнекамский нефтехимический колледж»
Галеев Э.Р., к.т.н., доцент, заместитель директора по НР НХТИ (филиал) ФГБОУ ВО «КНИТУ»
Мерзляков, С.А.
Основы теории управления в автоматизации нефтехимических производств : учебное пособие /, Д.В. Елизаров, С.А. Мерзляков. – Нижнекамск : Нижнекамский химико-технологический институт (филиал) ФГБОУ ВО «КНИТУ», 2016. – 67с.
В учебном пособии описаны основы алгоритмов и схем управления, показаны методы определения устойчивости замкнутых и разомкнутых систем, приведены алгоритмы определения настроек промышленных регуляторов
Пособие предлагается для студентов факультета управления и автоматизации, технологического и механического факультетов при выполнении курсовых и дипломных проектов, а также может быть полезным для инженерно-технических работников нефтехимических предприятий.
Пособие подготовлено на кафедре автоматизации технологических процессов и производств Нижнекамского химико-технологического института (филиал) ФГБОУ ВО «Казанский национальный исследовательский технологический университет»
УДК
© Елизаров Д.В., Мерзляков С.А., 2016
© Нижнекамский химико-технологический институт (филиал) ФГБОУ ВО «КНИТУ», 2016
Оглавление
1. ОБЩИЕ ПОНЯТИЯ ОБ УПРАВЛЕНИИ И СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 7
1.1. Основные понятия и определения. 7
1.2. Роль вычислительной техники в управлении процессами. 10
1.3. Управление процессом в реальном времени. 11
1.4. Генерация опорного значения. 13
1.5. Особенности систем цифрового управления. 13
1.6. Автоматическое и автоматизированное управления. 15
1.7. Основные принципы автоматического управления. 16
1.8. Основные виды систем автоматического управления. 18
2. ЛИНЕЙНЫЕ МОДЕЛИ И ХАРАКТЕРИСТИКИ СИСТЕМ УПРАВЛЕНИЯ 20
2.1. Математические модели объектов и систем управления. Модели типа вход – выход. 20
2.2. Составление математического описания объекта управления. 21
2.3. Линеаризация уравнения динамики. 22
2.4. Преобразование Лапласа. 25
2.5. Временные (переходные) характеристики. 29
2.6. Импульсная переходная функция. 30
2.7. Передаточная функция. 32
2.8. Частотные характеристики. 34
2.9. Динамические звенья и их характеристики. 37
2.10. Cтруктурный метод. 51
3. АНАЛИЗ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ УПРАВЛЕНИЯ.. 58
3.1. Анализ устойчивости. 58
3.2. Общее условие устойчивости. 59
3.3. Алгебраические критерии устойчивости. 64
3.4. Частотные критерии устойчивости. 66
3.5. Области и запасы устойчивости. 75
3.6. Управляемость и наблюдаемость. 83
3.7. Анализ переходных процессов в линейных системах автоматического управления. 84
3.8. Чувствительность систем управления. 94
3.9. Теория инвариантности и комбинированное управление. 96
3.10. Использование вычислительных машин. 98
4. СИНТЕЗ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ УПРАВЛЕНИЯ.. 100
4.1. Методы синтеза систем автоматического управления. 100
4.2. Типовые законы регулирования. 105
4.3. Расчет настроек промышленных регуляторов. 109
Генерация опорного значения
Обычно при регулировании необходимо поддерживать величину управляемого параметра в соответствии с опорным значением – уставкой, - которое постоянно пересчитывается во время протекания процесса. Вычисление уставки не должно иметь заметного запаздывания – каждое ее новое значение должно быть рассчитано до момента очередного сравнения с текущим значением управляемой величины (рис. 8).

Рис. 8. Генерация опорного значения
Система, отслеживающая значение опорного сигнала с достаточной быстротой и точностью, называется сервомеханизмом или, кратко, серво. В сервосистемах опорные значения либо рассчитываются, либо задаются в виде таблиц. Каждое вновь вычисленное опорное значение сравнивается с текущим положением. Затем компьютер посылает сигналы коррекции исполнительным механизмам.
Разомкнутое управление
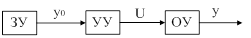
Рис. 10. Управление по задающему воздействию.
Такие САУ осуществляют управление только по задающему воздействию  . Такое управление называют жестким, т.к. при этом не учитываются действительные значения управляемой величины
. Такое управление называют жестким, т.к. при этом не учитываются действительные значения управляемой величины  и возмущающего воздействия
и возмущающего воздействия  . Подобные САУ дают удовлетворительное качество управления лишь при высокой стабильности параметров САУ и внешней среды и при невысоких требованиях к точности. По структуре такие САУ являются разомкнутыми, т.к. не имеют обратной связи по управляемому параметру
. Подобные САУ дают удовлетворительное качество управления лишь при высокой стабильности параметров САУ и внешней среды и при невысоких требованиях к точности. По структуре такие САУ являются разомкнутыми, т.к. не имеют обратной связи по управляемому параметру 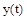 и не образуют замкнутого контура управления.
и не образуют замкнутого контура управления.
1.8.2. Принцип компенсации.
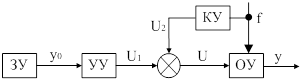
Рис. 11. Управление по возмущающему воздействию.
Управление по возмущению основано на принципе компенсации возмущения. Управляемый параметр не измеряется, а используется информация о внешнем воздействии  . При этом сначала определяют, какое возмущающее воздействие является основным, а затем устанавливают, как необходимо менять значение управляемого параметра при изменении данного возмущения, для того чтобы значение его поддерживать постоянным.
. При этом сначала определяют, какое возмущающее воздействие является основным, а затем устанавливают, как необходимо менять значение управляемого параметра при изменении данного возмущения, для того чтобы значение его поддерживать постоянным.
На рис. 11. КУ – корректирующие устройство, преобразующее возмущение  в дополнительное управляющее воздействие
в дополнительное управляющее воздействие 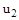 . Результирующий управляющий сигнал будет представлять собой сумму
. Результирующий управляющий сигнал будет представлять собой сумму 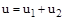 .
.
Достоинством принципа компенсации является быстрота реакции на возмущение. Недостаток – в случае преобладания неконтролируемых возмущений этот способ не дает требуемой точности.
Принцип обратной связи
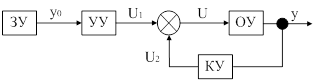
Рис. 12. Управление по отклонению.
Наибольшее распространение получил принцип обратной связи. Здесь управляющие воздействие корректируется в зависимости от выходной величины 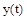 и уже не важно, какое возмущение действует на объект. Если значение
и уже не важно, какое возмущение действует на объект. Если значение  отклоняется от заданного значения, то происходит корректировка сигнала
отклоняется от заданного значения, то происходит корректировка сигнала 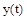 с целью уменьшение этого отклонения.
с целью уменьшение этого отклонения.
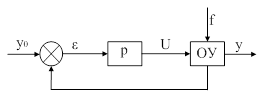
Рис. 13. Система автоматического регулирования.
Частным случаем САУ, работающих по принципу обратной связи, является система автоматического регулирования, представленная на рис. 13. Здесь 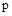 – регулятор, на вход которого поступает отклонение
– регулятор, на вход которого поступает отклонение 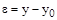 . Если
. Если  то регулятор не формирует управляющего воздействия. В случае, когда
то регулятор не формирует управляющего воздействия. В случае, когда 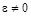 , вырабатывается управляющее воздействие
, вырабатывается управляющее воздействие 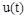 , направленное в сторону уменьшения сигнала рассогласования. При этом регулятор стремится компенсировать отклонение независимо от причин, вызвавших это отклонение. Такое управление можно назвать гибким, т.к. при этом учитывается действительное состояние объекта управления.
, направленное в сторону уменьшения сигнала рассогласования. При этом регулятор стремится компенсировать отклонение независимо от причин, вызвавших это отклонение. Такое управление можно назвать гибким, т.к. при этом учитывается действительное состояние объекта управления.
В качестве примера рассмотрим САР уровня воды в баке. (рис.14)

Рис. 14. САР уровня воды в баке.
Передаточная функция.
Частотные характеристики.
Статические звенья.
Все статические звенья в установившемся режиме описываются одинаковым уравнением  .
.
Интегрирующие звенья.
Дифференцирующие звенья.
Cтруктурный метод
Структурной схемой называется графическая модель системы, в которой каждому элементу ставится в соответствие его динамическая характеристика. Такая схема наглядно отражает состав системы и связи между отдельными ее составляющими.
Структурная схема может быть построена на основе, как дифференциальных уравнений, так и передаточных функций.

|
| Рис. 47. Структурная схема системы с параллельным соединением звеньев. |
Любая сложная структурная схема может быть изображена с помощью основных типов соединений:
· параллельное соединение;
· последовательное соединение;
· соединение с обратной связью.
Анализ устойчивости
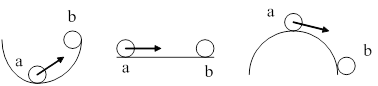
Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой. Существуют также нейтральные системы, которые после снятия возмущения приходят в состояние равновесия, отличное от исходного. Простейшие модели таких систем показаны на рис. 53.
|
| ||
| а) | б) | в) |
Рис. 53. Модели устойчивой (а), нейтральной (б) и неустойчивой (в) систем.
|
| |
| а) | б) |
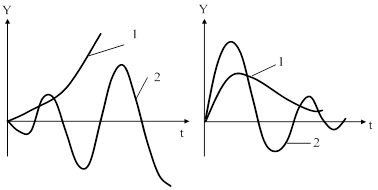
Рис. 54. Графики переходных процессов в неустойчивой (рис. а) и устойчивой (рис. б) системах.
На рис. 54 показаны типичные кривые переходных процессов. Если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния. Этот процесс может быть апериодическим (рис. а – кривая 1) или колебательным (кривая 2).
Апериодический расходящийся процесс может, например, возникнуть в САУ, если в ее управляющем устройстве ошибочно переключить полярность воздействия на объект, в результате чего управляющее устройство будет осуществлять не отрицательную, а положительную обратную связь вокруг объекта. При этом управляющее устройство будет не устранять отклонение 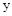 , а действовать в обратном направлении.
, а действовать в обратном направлении.
Колебательный расходящийся процесс может наступить, например, при неограниченном увеличении коэффициента передачи системы, вследствие чего управляющее устройство станет излишне энергично воздействовать на объект, стремясь ликвидировать первоначально возникшее отклонение 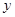 . В этом случае, при каждом очередном возврате
. В этом случае, при каждом очередном возврате  к нулю под действием управляющего устройства, кривая
к нулю под действием управляющего устройства, кривая 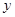 будет пересекать ось абсцисс все с большей скоростью и процесс в целом будет расходящимся.
будет пересекать ось абсцисс все с большей скоростью и процесс в целом будет расходящимся.
В случае устойчивой системы (рис. б) переходный процесс, вызванный каким-либо воздействием, со временем затухает апериодически (кривая 1) или колебательно (кривая 2) и система вновь возвращается в установившееся состояние.
Т.о. устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими.
Общее условие устойчивости.
Теоремы Ляпунова А.М.
Реальные системы являются, как правило, нелинейными.
Судить об устойчивости реальных систем можно по корням характеристического уравнения линеаризованных систем с помощью следующих теорем Ляпунова А.М.
Теорема 1: Если корни характеристического уравнения линеаризованной системы имеют отрицательную вещественную часть, то исходная реальная система устойчива.
Теорема 2: Если среди корней характеристического уравнения линеаризованной системы имеется хотя бы один корень с положительной вещественной частью, а остальные корни имеют отрицательную вещественную часть, то исходная реальная система неустойчива.
Теорема 3: Если среди коней характеристического уравнения линеаризованной системы имеется хотя бы один нулевой корень или одна пара чисто мнимых корней, то судить об устойчивости реальной системы нельзя, необходимо дальнейшее исследование.
Однако, на практике САУ рассчитываются с определенным запасом устойчивости. Поэтому в узкую область разделяющую линеаризованную систему от границы устойчивости, входит и граница устойчивости реальных систем. Поэтому можно сказать что в этом случае реальная система также будет находится на границе устойчивости.
Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости. Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости САУ) и частотные (основаны на исследовании частотных характеристик).
Критерий Гурвица.
Пусть система описывается дифференциальным уравнением 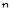 -го порядка (нумерация коэффициентов здесь проводится в обратном порядке по сравнению со стандартным дифференциальным уравнением)
-го порядка (нумерация коэффициентов здесь проводится в обратном порядке по сравнению со стандартным дифференциальным уравнением)

Составим из коэффициентов этого уравнения матрицу следующего вида
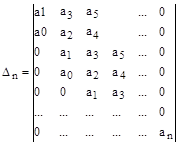 Матрица составляется по следующему правилу: в главной диагонали записывается подряд все коэффициенты, начиная с
Матрица составляется по следующему правилу: в главной диагонали записывается подряд все коэффициенты, начиная с  по
по 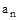 . Затем заполняются столбцы таким образом, чтобы над диагональю располагались подряд коэффициенты с возрастающими номерами, а под диагональю - с убывающими номерами. Свободные элементы матрицы заполняются нулями. В результате все нечетные строки содержат коэффициенты с нечетными номерами, а четные - только с четными, причем каждая следующая пара строк смещена по отношению к предыдущей на один столбец вправо.
. Затем заполняются столбцы таким образом, чтобы над диагональю располагались подряд коэффициенты с возрастающими номерами, а под диагональю - с убывающими номерами. Свободные элементы матрицы заполняются нулями. В результате все нечетные строки содержат коэффициенты с нечетными номерами, а четные - только с четными, причем каждая следующая пара строк смещена по отношению к предыдущей на один столбец вправо.
Для определителя 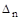 запишем диагональные миноры, которые называются определителями Гурвица.
запишем диагональные миноры, которые называются определителями Гурвица.
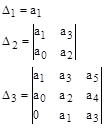
 В соответствии с критерием Гурвица, для того чтобы линейная система была устойчивой, необходимо и достаточно, чтобы все определители были положительными (при условии, что
В соответствии с критерием Гурвица, для того чтобы линейная система была устойчивой, необходимо и достаточно, чтобы все определители были положительными (при условии, что 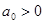 ).
).
Если хотя бы один определитель отрицательный, система будет не устойчива. Если один определитель равен нулю, а все остальные положительны, система находится на границе устойчивости.
Исходя из этого критерия, посмотрим, какие условия накладываются на коэффициенты дифференциальных уравнений I-го, II-го и III-го порядка.
1) 
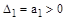
2) 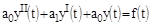

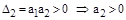
3) 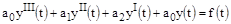
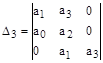

Таким образом, для систем I-го и II-го порядков необходимое условие устойчивости - положительность всех коэффициентов дифференциального уравнения – оказывается и достаточным. Для систем более высокого порядка этого условия недостаточно и на коэффициенты накладываются дополнительные ограничения. В частности, для систем III-го порядка произведение средних коэффициентов должно быть больше произведение крайних.
Пример 1.

 ,
, 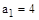 ,
,  ,
, 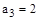 ,
, 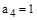
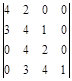
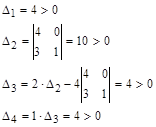

Поскольку все определители Гурвица больше нуля, система устойчива.
Пример 2.
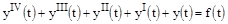
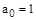 ,
, 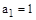 ,
, 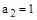 ,
,  ,
, 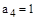
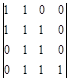
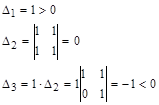
Система неустойчива, т.к. третий определитель отрицательный.
Принцип аргумента.
Запишем характеристический полином САУ в виде
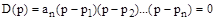
Его корни 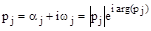 ,
,
где 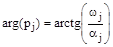 ;
; 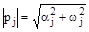 .
.
Каждый корень можно изобразить вектором на комплексной плоскости (рис. 57 а), тогда разность  изобразится разностью векторов (рис. 57 б), где
изобразится разностью векторов (рис. 57 б), где 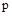 - любое число.
- любое число.
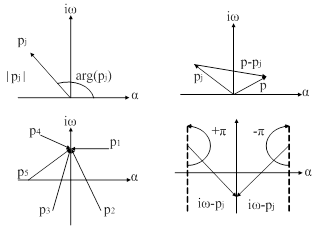
Рис. 57. Иллюстрация к принципу аргумента.
Если менять значение 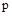 произвольным образом, то конец вектора
произвольным образом, то конец вектора 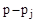 будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как
будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как 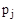 - это конкретное неизменное значение.
- это конкретное неизменное значение.
В частном случае, если на вход системы подавать гармонические колебания с различной частотой 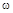 , то
, то 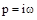 , а характеристический полином принимает вид:
, а характеристический полином принимает вид:
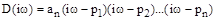
При этом концы векторов 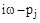 будут находиться на мнимой оси (рис. 57). Если менять
будут находиться на мнимой оси (рис. 57). Если менять 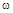 от -¥ до ¥, то каждый вектор
от -¥ до ¥, то каждый вектор 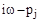 будет поворачиваться относительно своего начала
будет поворачиваться относительно своего начала 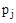 на угол
на угол 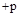 для левых и
для левых и 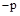 для правых корней (рис. 57).
для правых корней (рис. 57).
Характеристический полином можно представить в виде
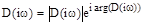 ,
,
uде  ;
;
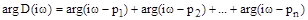
Пусть из 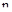 корней
корней 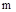 - правые, а
- правые, а 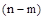 - левые, тогда угол поворота вектора
- левые, тогда угол поворота вектора 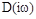 при изменении
при изменении  от -¥ до ¥ равен
от -¥ до ¥ равен
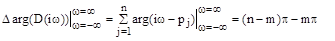
или при изменении 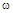 от 0 до ¥ получаем
от 0 до ¥ получаем
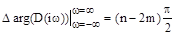
Отсюда вытекает правило: изменение аргумента вектора р при изменении частоты 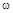 от -¥ до ¥ равно разности между числом левых и правых корней характеристического уравнения, умноженному на p, а при изменении частоты
от -¥ до ¥ равно разности между числом левых и правых корней характеристического уравнения, умноженному на p, а при изменении частоты 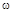 от 0 до ¥ эта разность умножается на p/2.
от 0 до ¥ эта разность умножается на p/2.
Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.
Критерий Михайлова.
Критерий был сформулирован А.В. Михайловым в 1938 г., он базируется на принципе аргумента функции комплексного переменного.
Также, как и алгебраический критерий, критерий Михайлова применяется в тех случаях, когда задано дифференциальное уравнение системы. В общем виде оно записывается следующим образом
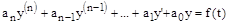 .
.
Для анализа устойчивости системы предлагается исследовать характеристический комплекс 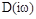 , который получается из характеристического полинома
, который получается из характеристического полинома
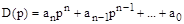
заменой  на
на 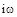 и имеет вид:
и имеет вид:
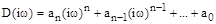 . (6)
. (6)
Выделим вещественную и мнимую части:
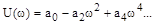 ,
, 
При конкретном численном значении частоты 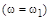 характеристический комплекс (6) представляет собой комплексное число
характеристический комплекс (6) представляет собой комплексное число 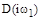 , которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой
, которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой 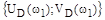 .
.
При изменении частоты 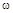 от 0 до ¥ конец вектора
от 0 до ¥ конец вектора  выписывает на комплексной плоскости некоторую кривую, которая называется годографом Михайлова. Причем начинается годограф, как следует из соотношения (6), в точке
выписывает на комплексной плоскости некоторую кривую, которая называется годографом Михайлова. Причем начинается годограф, как следует из соотношения (6), в точке 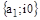 .
.
Формулировка критерия.
Замкнутая система устойчива, если годограф 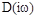 начинаясь при w = 0 на действительной положительной полуоси, огибает с рстом
начинаясь при w = 0 на действительной положительной полуоси, огибает с рстом 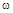 от 0 до ¥ против часовой стрелки начало координат, проходя последовательно в положительном направлении
от 0 до ¥ против часовой стрелки начало координат, проходя последовательно в положительном направлении  квадрантов, где
квадрантов, где 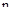 – порядок системы. При этом, изменение аргумента
– порядок системы. При этом, изменение аргумента 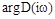 равно
равно 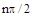 . В общем случае приращение аргумента составляет
. В общем случае приращение аргумента составляет 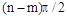 , где
, где 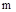 – число правых корней, но для устойчивой САУ
– число правых корней, но для устойчивой САУ 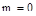 .
.
|
| |
| а) | б) |
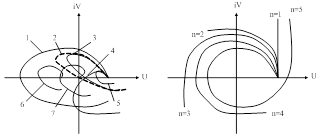
Рис. 58. Примеры годографов вектора Михайлова.
На рис. 58 а годограф 1 относится к устойчивой САУ, годографы 3, 4, 5, 6, 7 – к неустойчивым системам.
Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова через начало координат (кривая 2). В этом случае существует значение  , при котором
, при котором 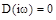 , т.е. характеристическое уравнение системы имеет пару комплексно сопряженных мнимых корней. Последнее означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате чего годограф
, т.е. характеристическое уравнение системы имеет пару комплексно сопряженных мнимых корней. Последнее означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате чего годограф 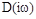 отойдет влево, или вниз от начала координат, делает систему устойчивой или нет.
отойдет влево, или вниз от начала координат, делает систему устойчивой или нет.
Следствие критерия Михайлова.
Система устойчива, если годограф Михайлова последовательно пересекает вещественную и мнимую оси, начинаясь на вещественной оси. Следовательно, необходимо и достаточно, чтобы точки пересечения годографа Михайлова положительной и отрицательной осей чередовались между собой.
На рис. 58 б приведены годографы устойчивых систем разных порядков до  .
.
При практическом построении годографа 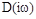 прежде всего находят точки его пересечения с координатными осями. Для этого, определив из уравнения
прежде всего находят точки его пересечения с координатными осями. Для этого, определив из уравнения 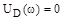 значения частот, соответствующие точкам пересечения годографа
значения частот, соответствующие точкам пересечения годографа  с мнимой осью, подставляют их в выражение
с мнимой осью, подставляют их в выражение  . В результате получают соответствующие ординаты. Аналогично находят точки пересечения
. В результате получают соответствующие ординаты. Аналогично находят точки пересечения  с действительной осью, приравнивая нулю мнимую часть
с действительной осью, приравнивая нулю мнимую часть 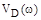 и подставляя затем найденные при этом значения
и подставляя затем найденные при этом значения 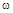 в выражение для
в выражение для 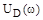 .
.
После того, как найдены значения частоты, при которых годограф  пересекает оси координат, т.е. найдены нули
пересекает оси координат, т.е. найдены нули 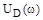 и
и 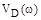 для суждения об устойчивости системы нет необходимости строить сам годограф.
для суждения об устойчивости системы нет необходимости строить сам годограф.
Пример 1.

Характеристическое уравнение для данной системы:
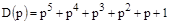
Вектор Михайлова получим из характеристического уравнения заменой  на
на 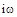 :
:
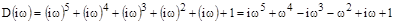 ;
;
 ,
, 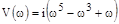 .
.
Перед построением всего годографа 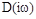 определим точки его пересечения с действительной и мнимой осями, т.е. найдем действительные и мнимые корни полиномов
определим точки его пересечения с действительной и мнимой осями, т.е. найдем действительные и мнимые корни полиномов 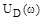 и
и 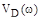 .
.
Найдем точку пересечения с мнимой осью 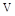 :
:
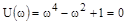

|
| Рис. 59. Иллюстрация к примеру. |
Это уравнение действительной корней не имеет, стало быть, годограф Михайлова не пересекает мнимую часть (рис. 59).
Дальнейший расчет можно не проводить, т.к. из первого заключения ясно, что система неустойчива. Действительно, по критерию Михайлова 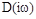 устойчивой системы 5-го порядка при изменении
устойчивой системы 5-го порядка при изменении  от 0 до ¥ должен пройти 5 квадрантов, начиная с 1-го, т.е. пересечь мнимую ось 2 раза.
от 0 до ¥ должен пройти 5 квадрантов, начиная с 1-го, т.е. пересечь мнимую ось 2 раза.
Пример 2. 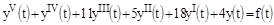
Характеристическое уравнение:
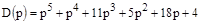 .
.
Вектор Михайлова:
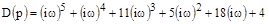
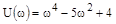 ;
;  .
.
Определим корни  и
и 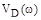 .
.
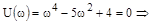
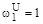 ,
, 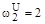
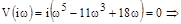
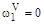 ,
, 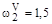
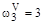 .
.
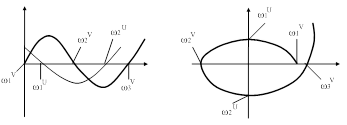
Расположив найденные корни на числовой оси (рис. 3.8 а), видим, что корни 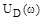 и
и 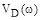 чередуются друг с другом, т.е. «критерий перемежаемости» выполняется. Полное исследование зависимости
чередуются друг с другом, т.е. «критерий перемежаемости» выполняется. Полное исследование зависимости  и
и 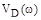 позволяет построить их графики и годограф
позволяет построить их графики и годограф  . Из годографа видно, что система устойчива.
. Из годографа видно, что система устойчива.
|
| |
| а) | б) |
Рис. 60. Построение годографа вектора Михайлова.
Метод D-разбиения
При создании реальной системы управления бывает необходимо знать не только запас устойчивости, который можно оценить с помощью какого-либо критерия, но и всю область устойчивости по параметрам. Этой цели служит метод D-разбиения, позволяющий построить такую область в плоскости одного или двух параметров системы.
Рассмотрим суть метода D-разбиения по одному параметру 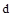 , который входит в характеристическое уравнение системы линейно:
, который входит в характеристическое уравнение системы линейно:
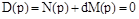
Заменив в этом уравнении  на
на 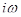 , получим уравнение
, получим уравнение
 ,
,
Решим его относительно 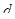 :
:
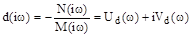 .
.
Получили комплексное представление параметра 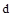 , что позволяет изобразить его в виде вектора на комплексной плоскости. Численное значение частоты определяет положение вектора
, что позволяет изобразить его в виде вектора на комплексной плоскости. Численное значение частоты определяет положение вектора 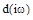 . При изменении
. При изменении 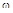 от
от 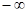 до
до  конец вектора выписывает на комплексной плоскости кривую D-разбиения, представляющую собой границу устойчивости (ее также можно рассматривать как отображение мнимой оси плоскости корней).
конец вектора выписывает на комплексной плоскости кривую D-разбиения, представляющую собой границу устойчивости (ее также можно рассматривать как отображение мнимой оси плоскости корней).

|
| Рис. 72. Пример кривой D-разбиения 1-3 – подобласти с различным распределением корней. |
Кривая D-разбиения симметрична относительно вещественной оси (рис. 72), поэтому достаточно построить ее часть, соответствующую положительным значениям частоты, а вторую половину получить отображением относительно вещественной оси.
Отметим, что эта кривая разбивает комплексную плоскость на несколько подобластей с различным соотношением корней. Для определения области устойчивости необходимо выбрать по одному значению 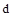 в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при конкретном
в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при конкретном 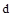 , то она будет устойчива и при всех его значениях из этой области.
, то она будет устойчива и при всех его значениях из этой области.
Обычно в качестве параметра 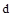 фигурирует реальный параметр системы (коэффициент усиления, постоянная времени, момент инерции и т д.), который может иметь только вещественные значения. Представление его комплексным выражением
фигурирует реальный параметр системы (коэффициент усиления, постоянная времени, момент инерции и т д.), который может иметь только вещественные значения. Представление его комплексным выражением 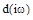 носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.
носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.
Метод D-разбиения можно применять и для построения области устойчивости по двум параметрам 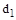 и
и 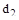 , которые входят линейно в характеристическое уравнение
, которые входят линейно в характеристическое уравнение
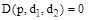
В этом случае уравнение границы устойчивости имеет вид
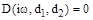
и распадается на два независимых уравнения
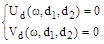
Эти два уравнения параметрически задают кривую D-разбиения. Область устойчивости определяется аналогично случаю одного параметра 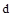 .
.
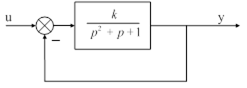
|
| Рис. 73. Структурная схема системы |
Пример.
Определить область устойчивости системы (рис. 73) по коэффициенту усиления.
Определим передаточную функцию замкнутой системы
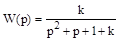
и запишем ее характеристическое уравнение
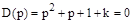 .
.
Здесь  - параметр, по которому строится область устойчивости, поэтому обозначим его через
- параметр, по которому строится область устойчивости, поэтому обозначим его через 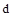 . Решим характеристическое уравнение относительно
. Решим характеристическое уравнение относительно 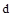 и заменим
и заменим 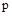 на
на  . В результате получим уравнение для кривой D-разбиения:
. В результате получим уравнение для кривой D-разбиения:
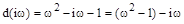
Вычислим значения вещественной и мнимой частей  при положительных значениях частоты и занесем их в таблицу.
при положительных значениях частоты и занесем их в таблицу.
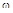
| 0 | 1 | 2 | ¥ | |
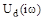
| -1 | 0 | 3 | ¥ | |

| 0 | -1 | -2 | -¥ |

|
| Рис. 74. Кривая D-разбиения для исследуемой системы |
Для построения всей кривой D-разбиения полученную половину 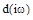 отобразим относительно оси абсцисс (рис. 74).
отобразим относительно оси абсцисс (рис. 74).
Как видим, кривая D-разбиения разделила плоскость параметра на две подобласти (1 и 2). Выбираем по одному вещественному значению 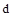 в каждой из них и оцениваем устойчивость.
в каждой из них и оцениваем устойчивость.
Исследуемая система имеет второй порядок, поэтому необходимым и достаточным условием ее устойчивости является положительность всех коэффициентов характеристического уравнения. Следовательно, первая область есть область устойчивости ( 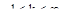 ), а вторая - неустойчивости.
), а вторая - неустойчивости.
Ошибка регулирования
Для оценки точности используется ошибка регулирования
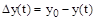 ,
,
которая с течением времени стремится к некоторому постоянному значению (рис. 75), называемому статической ошибкой:
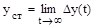 .
.
Таким образом, статическая ошибка равна разности между установившимся значением регулируемого параметра и его заданным значением.
| 
|
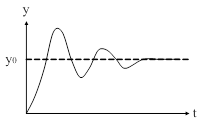
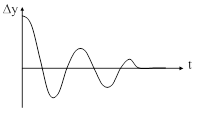
| Рис. 75. Пример изменения ошибки во времени | |
Динамической ошибкой будем называть величину, равную наибольшему отклонению регулируемой величины от ее установившегося значения:
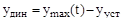 ,
,
Следует отметить, что ошибка (статическая ошибка) является одной из основных количественных характеристик процессов системы.
|
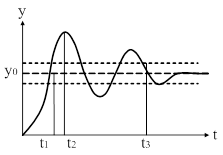
| Рис. 76. Иллюстрация оценок быстродействия. |
Быстродействие
В качестве оценок быстродействия можно использовать различные величины, причем все они определяют время от начала процесса до какого-либо характерного значения. С этой целью рассмотрим переходную характеристику системы 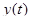 , изображенную на рис. 76.
, изображенную на рис. 76.
Оценками быстродействия могут служить:
· 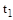 – время от начала процесса до первого момента достижения установившегося значения
– время от начала процесса до первого момента достижения установившегося значения 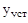 (применимо только для колебательных процессов);
(применимо только для колебательных процессов);
· 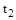 – время достижения первого максимума (также только для колебательных процессов);
– время достижения первого максимума (также только для колебательных процессов);
· 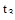 – время от начала переходного процесса до момента, когда отклонение выходной величины становится близким к установившемуся значению с заданной точностью
– время от начала переходного процесса до момента, когда отклонение выходной величины становится близким к установившемуся значению с заданной точностью 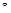 :
: 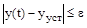 . Обычно в качестве
. Обычно в качестве 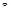 берут 5%-ое отклонение от
берут 5%-ое отклонение от 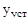 .
.
На практике в качестве оценки быстродействия чаще всего используют величину  , которую обычно обозначают
, которую обычно обозначают 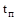 и называют временем переходного процесса.
и называют временем переходного процесса.
|
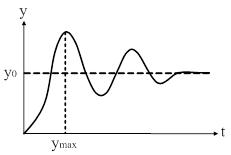
| Рис. 77. Иллюстрация оценки перерегулирования. |
Перерегулирование.
Эта количественная оценка характеризует колебательные свойства системы, обозначается буквой 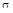 и определяется в процентах относительно установившегося значения (рис. 77) по выражению:
и определяется в процентах относительно установившегося значения (рис. 77) по выражению:
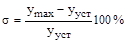 .
.
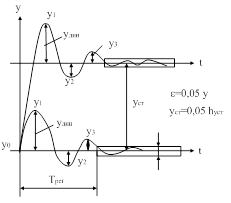
|
| Рис. 78. Показатели качества переходного процесса. |
Очевидно, чем больше перерегулирование 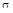 , тем более система склонна к колебаниям.
, тем более система склонна к колебаниям.
Все рассмотренные критерии могут отображены на графике переходного процесса следующим образом ( рис. 78):
Корневые методы.
Как было сказано выше, вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического управления. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая определенные условия на корни характеристического уравнения.
Для оценки быстродействия системы может использоваться понятие степени устойчивости.
Под степенью устойчивости 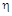 понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 79). Здесь могут быть два случая: когда ближайший корень является вещественным, (рис. 79 а) и когда к мнимой оси ближе всего расположена пара комплексных корней (рис. 79 б).
понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 79). Здесь могут быть два случая: когда ближайший корень является вещественным, (рис. 79 а) и когда к мнимой оси ближе всего расположена пара комплексных корней (рис. 79 б).
|
| |
| а) | б) |
Рис. 79. Расположение корней на комплексной плоскости.

|
| Рис. 80. Иллюстрация к понятию степени устойчивости. |
Корни характеристического уравнения, расположенные ближе всего к мнимой оси, т.е. имеющие наименьшую по абсолютной величине вещественную часть, дают в переходном процессе члены, которые затухают наиболее медленно.
Например, двум разным действительным корням 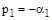 и
и 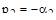 соответствуют две элементарные составляющие свободного движения системы (рис. 80):
соответствуют две элементарные составляющие свободного движения системы (рис. 80):
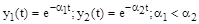 .
.
Очевидно, что чем меньше абсолютное значение корня, тем медленнее затухает составляющая переходного процесса.
Обратимся теперь к оценке запаса устойчивости системы автоматического управления. Склонность системы к колебаниям будет наблюдаться, если в решении характеристического уравнения будут присутствовать комплексные корни вида 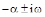 .
.
Степень колебательности m равна минимальному (для всех корней характеристического уравнения системы) модулю отношения действительной и мнимой частей корня, т.е.
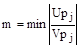
|
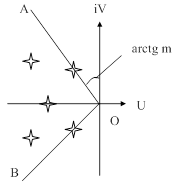
| Рис. 81. Иллюстрация к понятию степени колебательности переходного процесса. |
Поясним это определение. Если в плоскости корней характеристического уравнения устойчивой системы провести из начала координат два луча ОА и ОВ (рис. 81) таким образом, чтобы одна пара корней находилась на этих лучах, а все остальные корни лежали слева от них, то тангенс угла, заключенного между этими лучами и мнимой осью, будет равен отношению действительной и мнимой частей корней, лежащих на лучах ОА и ОВ, и являются степенью колебательности 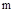 системы, т.к. для других корней это отношение будет больше, чем
системы, т.к. для других корней это отношение будет больше, чем 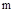 .
.
Колебательность связана с другим корневым показателем запаса устойчивости – с так называемым затуханием. Степень затухания определяется по формуле
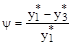 .
.
Между степенью затухания и степенью колебательности существует однозначная зависимость. Действительно, если
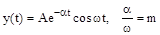 , то
, то
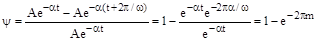 .
.
Очевидно, что степень затухания изменяется в пределах от 0 до 1, а степень колебательности – от 0 до ¥. Наиболее часто используемые значения лежат в пределах от 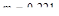 (
( 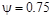 ) до
) до 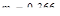 (
( 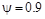 ).
).
Корневой метод
Наиболее простой метод разработал Т.Н.Соколов. Сущность его сводится к следующему.
Пусть имеется характеристическое уравнение системы:
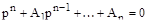 (10)
(10)
С точки зрения скорейшего затухания переходного процесса важно, чтобы вещественные части всех корней характеристического уравнения были наибольшими. Сумма вещественных частей всех корней численно равна первому коэффициенту характеристического уравнения. Поэтому при заданной величине этого коэффициента наиболее лучшие результаты получаются при равенстве вещественных частей всех корней. Однако расчеты и исследования построенных систем показывают, что стремление удовлетворить поставленному требованию приводит к совершенно нереальным конструктивным характеристикам отдельных звеньев. Эти расчеты и исследования показывают, что из общего числа корней характеристического уравнения всегда можно выделить два или три корня с меньшей по абсолютному значению вещественной частью, которые и определяют ход основного процесса. Остальные же корни характеризуют быстро затухающие составляющие, оказывающие влияние только на начальной стадии переходного процесса.
Примем, что основной характер переходного процесса определяется двумя корнями. тогда уравнение (10) удобно представить в виде
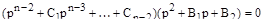
 (11)
(11)
Второй сомножитель (11) и будет определять основной характер процесса.
Для уменьшения погрешностей проектируемой системы важно, чтобы коэффициент  в основном множителе имел возможно большую величину. Однако чрезмерное увеличение
в основном множителе имел возможно большую величину. Однако чрезмерное увеличение  приводит к колебательному характеру переходного процесса.
приводит к колебательному характеру переходного процесса.
Оптимальное соотношение между коэффициентами 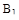 и
и  определяется из условия получения затухания за один период
определяется из условия получения затухания за один период 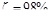 (см. Бесекерский стр. 206), которому соответствует выражение
(см. Бесекерский стр. 206), которому соответствует выражение
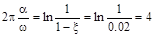 (12)
(12)
где  и
и 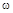 – вещественная и мнимая части комплексного корня, характеризующего основной процесс.
– вещественная и мнимая части комплексного корня, характеризующего основной процесс.
Учитывая соотношения:
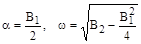
из (12) можно получить: 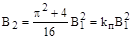
Множитель 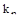 , определяющий соотношение между коэффициентами основного множителя характеристического уравнения, является критерием переходного режима, зависящим от выбранной степени затухания. Последняя формула показывает желаемое соотношение между коэффициентами характеристического уравнения, к которому надо стремится при проектировании системы. Это должно осуществляться введением различных корректирующих средств.
, определяющий соотношение между коэффициентами основного множителя характеристического уравнения, является критерием переходного режима, зависящим от выбранной степени затухания. Последняя формула показывает желаемое соотношение между коэффициентами характеристического уравнения, к которому надо стремится при проектировании системы. Это должно осуществляться введением различных корректирующих средств.
Из (12) можно также получить требуемые соотношения между мнимой и вещественной частями корня (колебательность):
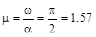 .
.
Метод корневых годографов.
Качество системы управления с точки зрения быстродействия и запаса устойчивости может характеризоваться расположением корней числителя и знаменателя передаточной функции замкнутой системы, т.е. расположением нулей и полюсов передаточной функции.
Зная эти корни, можно изобразить их расположение на комплексной плоскости корней. При расчете системы целесообразно проследить, как меняется картина расположения корней при изменении отдельных параметров, например коэффициента передачи разомкнутой системы, постоянных времени корректирующих цепей и т.д., с целью установления оптимальных значений этих параметров.
При плавном изменении значения какого либо параметра корни будут перемещаться на плоскости корней, прочерчивая некоторую кривую, которую будем называть корневым годографом или траекторией корней. Построив траектории всех корней, можно выбрать такое значение варьируемого параметра, которое соответствует наилучшему расположению корней.
Один из способов построения траекторий корней заключается в следующем. Пусть имеется передаточная функция замкнутой системы:
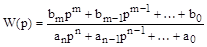
Полюсы передаточной функции, т.е. корни знаменателя, обозначим через 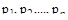 , а нули (корни числителя) – через
, а нули (корни числителя) – через 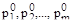 .
.
Коэффициенты числителя и знаменателя определенным образом выражены через параметры объекта, управляющего устройства и корректирующих устройств. Если нужно выбрать величину какого-либо параметра 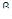 (постоянная времени, коэффициент усиления и т.д.), входящего как угодно в коэффициенты передаточной функции, то необходимо принять некоторые постоянные значения для всех остальных параметров, а для искомого параметра
(постоянная времени, коэффициент усиления и т.д.), входящего как угодно в коэффициенты передаточной функции, то необходимо принять некоторые постоянные значения для всех остальных параметров, а для искомого параметра 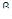 задавать различные числовые значения
задавать различные числовые значения 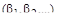 внутри реально возможных пределов изменения этого параметра в данной системе. Для каждого из этих вариантов необходимо затем вычислить корни числителя и знаменателя. Результаты вычислений можно свести в таблицу, на основании которой легко строятся все траектории корней.
внутри реально возможных пределов изменения этого параметра в данной системе. Для каждого из этих вариантов необходимо затем вычислить корни числителя и знаменателя. Результаты вычислений можно свести в таблицу, на основании которой легко строятся все траектории корней.
Если нужно выбрать два или несколько параметров системы, то такого рода вычисления нужно проделать несколько раз, меняя каждый раз один параметр при заданных значениях всех остальных.
Вычисление корней при этом можно производить при помощи стандартных программ для цифровых машин с выводом корневого годографа на экран дисплея.
Построение желаемой ЛАЧХ.
Построение желаемой ЛАЧХ делается на основе трех требований, которые предъявляются к проектируемой системе управления. При построении желаемой ЛАЧХ необходимо быть уверенным, что вид амплитудной характеристики полностью определяет характер переходных процессов и нет необходимости вводить в рассмотрение фазовую характеристику. Это будет выполняться в случае минимально-фазовых систем. В этом случае амплитудная характеристика однозначно определяет вид фазовой характеристики. Напомним, что передаточная функция разомкнутой минимально-фазовой системы не должна иметь нулей и полюсов, расположенных в правой полуплоскости.
Метод РАФХ.
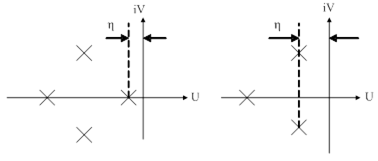
Согласно критерия Найквиста, если АФХ устойчивой разомкнутой системы проходит через критическую точку  , то замкнутая система находится на границе устойчивости. В качестве границы устойчивости выступает мнимая ось комплексной плоскости корней характеристического уравнения. Введение степени колебательности
, то замкнутая система находится на границе устойчивости. В качестве границы устойчивости выступает мнимая ось комплексной плоскости корней характеристического уравнения. Введение степени колебательности  для получения РАФХ означает введение новой границы устойчивости вместо мнимой оси лучи AOB (рис. 92).
для получения РАФХ означает введение новой границы устойчивости вместо мнимой оси лучи AOB (рис. 92).
Аналогично критерия Найквиста можно сформулировать условия для достижения замкнутой системой заданной степени колебательности 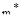 .
.
Если разомкнутая система имеет степень колебательности не ниже заданного значения 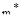 , то замкнутая система обладает заданной степенью колебательности
, то замкнутая система обладает заданной степенью колебательности 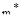 , если РАФХ разомкнутой системы проходит через критическую точку
, если РАФХ разомкнутой системы проходит через критическую точку  ; если РАФХ разомкнутой системы не охватывает критическую точку
; если РАФХ разомкнутой системы не охватывает критическую точку  , то замкнутая система имеет степень колебательности выше заданного значения
, то замкнутая система имеет степень колебательности выше заданного значения 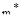 .
.
Если РАФХ разомкнутой системы имеет степень колебательности ниже заданного значения 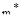 , то замкнутая система будет обладать заданным значением степени колебательности
, то замкнутая система будет обладать заданным значением степени колебательности 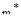 , если РАФХ разомкнутой системы охватывает критическую точку
, если РАФХ разомкнутой системы охватывает критическую точку  столько раз, сколько корней характеристического уравнения располагается правее лучей АОВ. Из сформулированного условия можно записать:
столько раз, сколько корней характеристического уравнения располагается правее лучей АОВ. Из сформулированного условия можно записать:
 ;
;
Учитывая, что 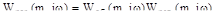 ; (разомкнутая система будет представлена последовательным соединением объекта и регулятора).
; (разомкнутая система будет представлена последовательным соединением объекта и регулятора).
Подставим в предыдущее уравнение и получим:
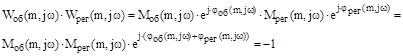
Отсюда:
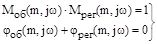
Частотные характеристики объекта и заданная степень колебательности являются исходными данными для расчета АСР, характеристики регулятора являются функцией неизвестных параметров настройки 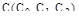 . Тогда система уравнений запишется в виде:
. Тогда система уравнений запишется в виде:
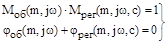 (13)
(13)
Анализ системы уравнений показывает, что одного заданного значения степени колебательности 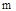 является недостаточно для расчета настроек регулятора. Для определения оптимальных настроек вводится новый критерий – интегральный квадратичный критерий. Задача будет формулироваться так:
является недостаточно для расчета настроек регулятора. Для определения оптимальных настроек вводится новый критерий – интегральный квадратичный критерий. Задача будет формулироваться так:
Рассчитать оптимальные настройки регулятора из условия минимума интегрального квадратичного критерия при заданной степени колебательности. Эта задача решается в два этапа.
На первом этапе задача выбора оптимальных настроек регулятора сводится к решению системы уравнений (13), неизвестными в которых являются вектор параметров настроек 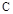 и рабочая частота
и рабочая частота 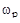 .
.
Очевидно, что для регуляторов с двумя или тремя параметрами настроек эта система уравнений имеет бесчисленное множество решений. Это означает, что одного только ограничения по степени колебательности недостаточно для однозначного выбора оптимальных настроек регулятора и требуется какой-либо второй критерий качества.
При использовании метода расширенных частотных характеристик таким критерием выбран интегральный квадратичный критерий, для которого оптимальные настройки должны обеспечивать минимальное значение.
Таким образом на втором этапе расчета оптимальные настройки выбирают по минимуму интегрального критерия из числа тех настроек, которые обеспечивают заданную степень колебательности системы, т.е. являются решением уравнений (13). Рассмотрим подробнее методику выбора оптимальных настроек для типовых регуляторов.
П – регулятор имеет один параметр настройки 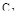 . Его расширенные частотные характеристики совпадают с обычными, т.е.
. Его расширенные частотные характеристики совпадают с обычными, т.е.
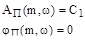
В этом случае уравнения (13) принимают вид:

Рабочая частота 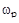 определяется из второго уравнения системы, а затем из первого находится оптимальная настройка
определяется из второго уравнения системы, а затем из первого находится оптимальная настройка 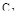 .
.
ПИ – регулятор – регулятор с двумя параметрами настроек  и
и  . Его расширенные частотные характеристики выводятся из передаточной функции подстановкой
. Его расширенные частотные характеристики выводятся из передаточной функции подстановкой 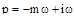 :
:
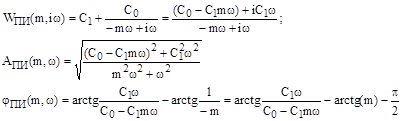
с учетом того, что 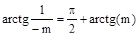 .
.
После подстановки полученных выражений в уравнения (13) выводятся формулы для настроек регуляторов в следующем виде:
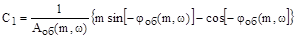
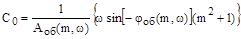 .
.

|
| Рис. 93. Плоскость параметров настроек ПИ-регулятора. |
Поскольку в формулы для настроек входит неизвестная переменная 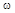 , то, следовательно, существует бесчисленное множество настроек
, то, следовательно, существует бесчисленное множество настроек 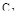 и
и  , обеспечивающих заданную степень колебательности в данной АСР, причем каждой паре настроек соответствует своя рабочая частота.
, обеспечивающих заданную степень колебательности в данной АСР, причем каждой паре настроек соответствует своя рабочая частота.
Если в плоскости параметров 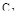 ,
, 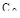 построить геометрическое место точек, соответствующих определенной степени колебательности
построить геометрическое место точек, соответствующих определенной степени колебательности 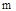 , получим кривую, называемую кривой равной колебательности (рис. 93).
, получим кривую, называемую кривой равной колебательности (рис. 93).
Принимая различные значения m, получим семейство кривых равной колебательности, каждая из которых разбивает плоскость параметров на две области: настройки, лежащие под кривой 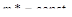 , обеспечивает себе степень колебательности, больше
, обеспечивает себе степень колебательности, больше  ; область, расположенная под этой кривой, соответствует степени колебательности, меньшей, чем
; область, расположенная под этой кривой, соответствует степени колебательности, меньшей, чем 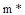 . Очевидно, что кривая
. Очевидно, что кривая  разбивает плоскость параметров настроек регулятора на области устойчивой и неустойчивой работы АСР.
разбивает плоскость параметров настроек регулятора на области устойчивой и неустойчивой работы АСР.
Точки, лежащие на кривой равной колебательности, соответствует разным значениям рабочей частоты, причем при движении вдоль кривой слева направо частота увеличивается.
Сравним между собой процессы регулирования, соответствующие различным точкам на кривой равной колебательности (рис. 93, 94).
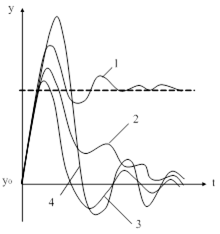
|
| Рис. 94. Примеры переходных процессов в АСР с ПИ-регулятором. |
В точке 1 отсутствует интегральная составляющая в законе регулирования  и в процессе регулирования появляется статическая ошибка. При незначительной интегральной составляющей (точка 2) статическая ошибка равна нулю, но скорость ее устранения мала и переходный процесс характеризуется затянутым «хвостом». Увеличение интегральной составляющей ускоряет устранение статической ошибки, но сопровождается уменьшением рабочей частоты (движением влево по кривой равной колебательности) и некоторым ростом динамической ошибки (точка 4). Переход через вершину кривой влево (точка 5) резко ухудшает качество переходного процесса, так как одновременно с уменьшением
и в процессе регулирования появляется статическая ошибка. При незначительной интегральной составляющей (точка 2) статическая ошибка равна нулю, но скорость ее устранения мала и переходный процесс характеризуется затянутым «хвостом». Увеличение интегральной составляющей ускоряет устранение статической ошибки, но сопровождается уменьшением рабочей частоты (движением влево по кривой равной колебательности) и некоторым ростом динамической ошибки (точка 4). Переход через вершину кривой влево (точка 5) резко ухудшает качество переходного процесса, так как одновременно с уменьшением 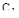 уменьшается и
уменьшается и 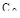 .
.
Расчет интегрального квадратичного критерия для рассмотренных процессов показывает, что его минимум соответствует точке на кривой равной колебательности на правой ветви вблизи вершины. На практике рекомендуется выбирать рабочую частоту из соотношения: 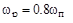 или
или 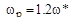 , где
, где  – частота, соответствующая П – регулятору (точка 1);
– частота, соответствующая П – регулятору (точка 1);  - частота, соответствующая вершине кривой равной колебательности.
- частота, соответствующая вершине кривой равной колебательности.
Таким образом, методика расчета оптимальных настроек ПИ – регулятора сводится к следующему:
- расчет расширенных частотных характеристик объекта для заданной степени колебательности  ;
;
- расчет и построение кривой равной колебательности  в плоскости параметров
в плоскости параметров 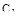 и
и 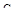 по формулам;
по формулам;
- выбор рабочей частоты 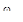 и соответствующих ей оптимальных настроек.
и соответствующих ей оптимальных настроек.
ПД – регулятор так же, как и ПИ – регулятор, имеет два параметра настроек –  и
и 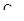 , поэтому процедура расчета этих регуляторов аналогична. В соответствии с изложенной методикой выведем расчетные формулы для ПД – регулятора.
, поэтому процедура расчета этих регуляторов аналогична. В соответствии с изложенной методикой выведем расчетные формулы для ПД – регулятора.
Расширенные частотные характеристики ПД – регулятора имеют вид:
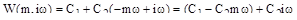 ;
;
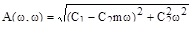 ;
;
 .
.
Решение системы уравнений дает следующие выражения для настроек регулятора:
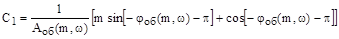 ,
,
 .
.
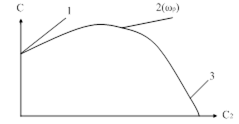
|
| Рис. 95. Плоскость параметров настроек ПД – регулятора. |
Кривая равной колебательности рассчитывается по последним формулам и строится в плоскости 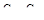 . Типичная картина разбиения плоскости параметров ПД – регулятора кривыми равной колебательности приведена на рис. 95.
. Типичная картина разбиения плоскости параметров ПД – регулятора кривыми равной колебательности приведена на рис. 95.
Движение вдоль кривой вправо, при котором растет дифференциальная настройка, сопровождается увеличением рабочей частоты и, следовательно, уменьшением динамической ошибки. Однако при этом статическая ошибка сначала уменьшается (пока растет пропорциональная составляющая), а затем увеличивается (на правой ветви кривой).

|
| Рис. 96. Примеры процессов регулирования. |
Таким образом, оптимальные настройки ПД – регулятора соответствуют вершине кривой равной колебательности.
На рис. 96 приведены примеры переходных процессов в АСР с ПД – регулятором при различных настройках.
ПИД – регулятор имеет три параметра настроек 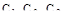 и поэтому его расчет по методу расширенных частотных характеристик несколько сложнее, чем расчет регуляторов с двумя параметрами.
и поэтому его расчет по методу расширенных частотных характеристик несколько сложнее, чем расчет регуляторов с двумя параметрами.
Расширенные частотные характеристики ПИД – регулятора:
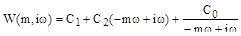 ;
;
 ;
; 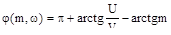 ;
;
где 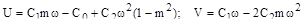 .
.
Решение системы уравнений с учетом последних формул дает выражения для расчета двух настроек как функции третьей настройки, например:
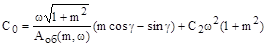 ;
;
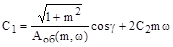 ,
,
где 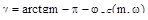 .
.
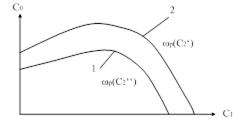
Для ПИД – регулятора вместо плоскости параметров настроек мы имеем трехмерное пространство. В этом случае определение оптимальных настроек производится в следующем порядке.
|
| Рис. 97. Плоскость параметров настроек ПИД – регулятора. |
Задаваясь различными значениями настройки 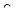 , по последним формулам рассчитываем кривые равной колебательности в плоскости
, по последним формулам рассчитываем кривые равной колебательности в плоскости 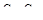 (рис. 97). Характер этих кривых аналогичен рассмотренной ранее кривой для ПИ – регулятора, который получается как частный случай из ПИД – регулятора при
(рис. 97). Характер этих кривых аналогичен рассмотренной ранее кривой для ПИ – регулятора, который получается как частный случай из ПИД – регулятора при  . Условно оптимальные настройки находятся также как и для ПИ – регулятора.
. Условно оптимальные настройки находятся также как и для ПИ – регулятора.
|
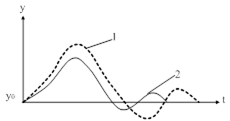
| Рис. 98. Примеры процессов регулирования. |
Сравнение между собой оптимальных процессов регулирования для разных значений 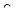 показывает, что введение дифференциальной составляющей в закон регулирования (по сравнению с ПИ – регулятором) существенно улучшает качество переходных процессов (рис. 98).
показывает, что введение дифференциальной составляющей в закон регулирования (по сравнению с ПИ – регулятором) существенно улучшает качество переходных процессов (рис. 98).
Однако, начиная с некоторых значений 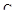 , дальнейшее его увеличение малоэффективно. поэтому окончательный выбор оптимального значения
, дальнейшее его увеличение малоэффективно. поэтому окончательный выбор оптимального значения 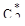 и соответствующих ему
и соответствующих ему  и
и 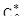 должен производиться на основе непосредственного сравнения качества процессов регулирования по интегральному квадратичному критерию.
должен производиться на основе непосредственного сравнения качества процессов регулирования по интегральному квадратичному критерию.
Нижнекамский химико-технологический институт (филиал)
Федерального государственного бюджетного образовательного учреждения высшего образования
«Казанский национальный исследовательский технологический университет»
Дата: 2019-02-19, просмотров: 412.