Справочный материал для учителя
В формулировке правила содержатся термины «длина» и «ширина». По поводу этих терминов сделаем одно разъяснение. Длину прямоугольника обычно связывают с большей его стороной, а ширину – с меньшей. Иногда в упражнениях содержится требование найти площадь прямоугольника, если даны длины сторон, например 4 см и 6 см. В таких случаях учащиеся должны понимать, что для вычисления площади прямоугольника надо перемножить числа 4 и 6. (можно в любом порядке.)
Для квадрата правило нахождения его площади отдельно не формулируется. Выясните у учащихся почему. (Так как квадрат – это прямоугольник, то для вычисления его площади можно пользоваться правилом вычисления площади прямоугольника.)
Выясните также, что надо перемножать при вычислении площади квадрата. (Так как у квадрата длина равна ширине, то для нахождения его площади достаточно перемножить две длины.)
* * *
Задание № 1 (с. 87).
Сначала учитель вводит термины «длина» и «ширина» прямоугольника. (Начертите заранее на доске любой прямоугольник, расположив его произвольно.)
Покажите две смежные стороны этого прямоугольника и назовите большую из них длиной, а меньшую – шириной прямоугольника.
– Измерьте длину и ширину прямоугольника.
– Какова площадь прямоугольника?
– Как найти площадь прямоугольника вычислением?
Учитель знакомит учащихся с правилом в учебнике (на с. 87).
Задание № 2 (с. 87).
Перед выполнением упражнения учитель проводит беседу.
– Как называется первая фигура? (Прямоугольник.)
–Какие измерения необходимо выполнить, чтобы найти площадь прямоугольника? (Нужно измерить длину и ширину.)
– Как называется вторая фигура? (Квадрат.)
– Какие измерения необходимо выполнить, чтобы найти площадь квадрата? (Достаточно измерить длину только одной стороны.)
Далее учащиеся работают самостоятельно.
Запись:
1) 6 · 2 = 12 (см2) – площадь прямоугольника.
2) 3 · 3 = 9 (см2) – площадь квадрата.
Ответ: 12 см2, 9 см2.
V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 169.
Правильный чертеж к заданию следующий:
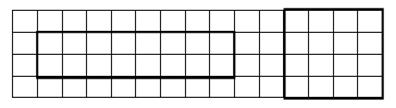
Стороны прямоугольника: 1 см, 4 см.
Сторона квадрата: 2 см.
2. Работа по учебнику.
Задание № 7 (с. 88).
Учащиеся составляют схемы-«машины»:
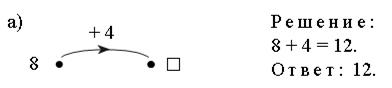

Задание № 8 (с. 88).
Учащиеся составляют схемы-«машины»:
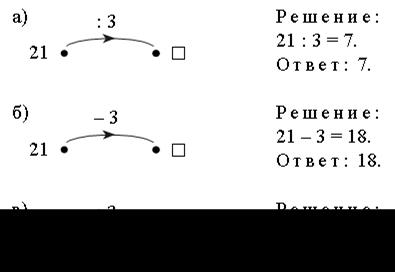
– Задаем вопросы: «Во сколько раз 3 меньше, чем 21?» и «Во сколько раз 21 больше, чем 3?»
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить площадь прямоугольника?
– Назовите единицы измерения площади.
Домашнее задание: № 9 (учебник); № 167 (рабочая тетрадь).
Урок 117
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
Цели: формировать умения пользоваться правилом вычисления площади прямоугольника (квадрата); совершенствовать умения решать составные задачи разными способами; закреплять знания определений геометрических фигур; развивать внимание и умение анализировать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Геометрия на спичках.
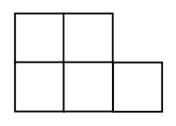
а) Уберите четыре палочки так, чтобы осталось 2 квадрата.
б) Уберите четыре палочки так, чтобы остался 1 квадрат.
в) Уберите пять палочек так, чтобы осталось 3 квадрата.
г) Переложите две палочки так, чтобы стало 8 квадратов.
д) Переложите две палочки так, чтобы стало 7 квадратов.
е) Переложите две палочки так, чтобы стало 6 квадратов.
2. Поставьте знаки «+» или «–».
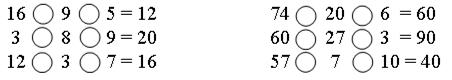
3. Задача.
В первый день посадили 20 саженцев, во второй – на 10 саженцев больше, чем в первый, а в третий – на 18 саженцев больше, чем во второй. Сколько саженцев посадили в третий день?
III. Сообщение темы урока.
– Сегодня на уроке будем решать задачи на нахождение площади прямоугольников.
IV. Работа по теме урока.
Задание № 3 (с. 87).
– Как вычислить площадь прямоугольника?
– Что необходимо знать?
Далее учащиеся выполняют вычисления. Запись можно оформить в таблице.
| Длина | Ширина | Площадь | |
| I | 5 дм | 3 дм | Решение: 5 · 3 = 15 (дм2) |
| II | 9 см | ? на 2 см м. | 1) 9 – 2 = 7 (см) 2) 9 · 7 = 63 (см2) |
| III | ?, в 2 раза б. | 4 см | 1) 4 · 2 = 8 (см) 2) 8 · 4 = 32 (см2) |
| IV | 4 дм | 40 см 40 см = 4 дм | 4 · 4 = 16 (дм2) |
Задание № 4 (с. 88).
– Какая фигура изображена на чертеже?
– Что известно по данному чертежу? (Площадь и ширина прямоугольника.)
– Что требуется узнать? (Длину прямоугольника.)
– Запишите условие задачи в таблицу:
| Длина | Ширина | Площадь |
| ? см | 2 см | 16 см2 |
Решение:
16 : 2 = 8 (см) – длина.
Ответ: 8 см.

Дата: 2018-12-28, просмотров: 686.