Задание № 1 (с. 83).
– Как называется данная фигура?
– Назовите признаки прямоугольника.
– Измерьте длину каждой стороны прямоугольника.
– Какой вывод можно сделать? (В прямоугольнике длины противоположных сторон равны.)
АВ = СД = 3 см.
ВС = АД = 4 см.
Далее учащиеся читают определение в учебнике (на с. 83).
Задание № 2 (с. 83).
– Рассмотрите данный чертеж.
– Назовите диагонали прямоугольника. (отрезки АС и ВД – диагонали.)
– Измерьте длину каждой диагонали прямоугольника.
– Какой вывод можно сделать? (Длины диагоналей прямоугольника равны.) АС = ВД.
Далее учащиеся читают правило в учебнике (на с. 83).
Задание № 3 (с. 84).
Лучше всего выполнить упражнение устно, подробно разбирая каждый пункт задания. При этом просите детей давать подробные и обоснованные ответы.
1. Учащееся могут предложить два общих названия фигур: многоугольник и четырехугольник. Обязательно задайте дополнительный вопрос: «Какое из этих названий точнее?» (Четырехугольник.)
2. У фигур 1 и 2 все углы прямые, а у фигуры 3 нет прямых углов. (Учащиеся проверяют это с помощью чертежного угольника.)
3. Так как фигуры 1 и 2 – четырехугольники, у которых все углы прямые, то их можно назвать прямоугольниками.
4. У фигуры 2, в отличие от фигуры 1, все стороны равны. (Учащиеся проверяют это с помощью циркуля.)
5. Так как фигура 2 – прямоугольник, у которого все стороны равны, то ее можно назвать квадратом.
6. Так как фигура 1 – прямоугольник, то у нее противоположные стороны равны.
7. У фигуры 2 все стороны равны.
В заключение учитель задает дополнительные вопросы:
– Любой ли квадрат является прямоугольником? (Да, любой, так как квадрат по определению – прямоугольник.)
– Любой ли прямоугольник является квадратом? (Нет, не любой прямоугольник является квадратом, а лишь тот, у которого все стороны имеют одну и ту же длину.)

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 162.
Чертеж:
АВ = 2 см
ВС = 4 см
СД = 2 см
АД = 4 см
– Как называется отрезок АС в прямоугольнике АВСД? (Диагональ.)
– Проведите вторую диагональ. (ВД.)
– Что вы знаете о длинах диагоналей прямоугольника?
Задание № 163.
Чертеж к заданию:
Каждый из образовавшихся квадратов составляет половину прямоугольника.
2. Работа по учебнику.
Задание № 10 (с. 85).
Учащиеся составляют схему-«машину».
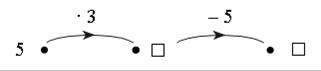
Решение:
1) Чему равно второе число?
5 · 3 = 15.
2) Чему равна разность двух чисел?
15 – 5 = 10.
Ответ: 10.
Задание № 11 (с. 85).

VI. Итог урока.
– Что нового узнали на уроке?
– Назовите свойства прямоугольника.
Домашнее задание: № 8, 9 (учебник); № 160, 161 (рабочая тетрадь).
Урок 115
СВОЙСТВА ПРЯМОУГОЛЬНИКА
Цели: продолжить формирование умений решать геометрические задачи, используя основные свойства прямоугольника; совершенствовать вычислительные навыки; развивать внимание и мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
а) Число 8 умножьте на 6. Разделите 35 на 7. Сложите 16 и 8. Из 42 вычтите 11.
б) Увеличьте 12 на 8 и из результата вычтите 4. Уменьшите 17 на 7 и к результату прибавьте 50. Увеличьте 9 в 8 раз и к результату прибавьте 8. Уменьшите 42 в 7 раз и результат увеличьте в 48 раз.
2. Задача.
По таблице составьте три задачи и решите их.
| Было | 15 м. | ? | 18 м. |
| Уехало | 8 м. | 9 м. | ? |
| Осталось | ? | 3 м. | 10 м. |
3. Заполните свободные клетки таблицы.
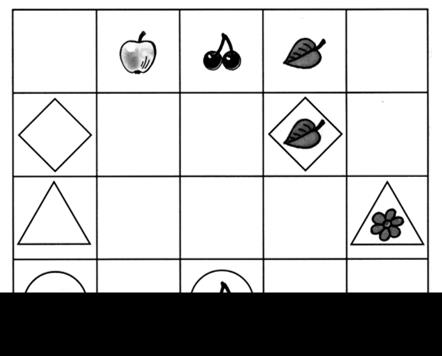
III. Сообщение темы урока.
– Сегодня на уроке будем решать геометрические задачи.
IV. Работа по теме урока.
Задание № 4 (с. 84).
Задание направлено прежде всего на дальнейшее уточнение знаний о диагоналях прямоугольника (квадрата).
В результате выполнения этого упражнения учащиеся должны сделать следующие основные выводы:
1) у прямоугольника, не являющегося квадратом, диагональ не является осью симметрии, а у квадрата диагональ – ось симметрии;
2) у квадрата, так же как и у любого прямоугольника, диагонали равны.
Задание № 5 (с. 84).
Это задание выполняется устно (фронтальная работа).
Задание № 6 (с. 85).
Учащиеся, используя зеркало, проверяют, симметричны ли противоположные вершины квадрата относительно его диагоналей.
Задание № 7 (с. 85).
Задание продолжает серию упражнений, направленных на формирование у учащихся умения выполнять логическую операцию «подведение под определение». Для того чтобы фигура была квадратом, необходимо выполнение двух условий:
1) фигура должна быть прямоугольником;
2) у нее все стороны должны иметь одну и ту же длину.
В данном случае описывается именно такая фигура (прямоугольник, длина каждой стороны которого равна 9 см). Значит, это квадрат.

Дата: 2018-12-28, просмотров: 693.