1. Работа по учебнику.
Задание № 22 (с. 55).
Это логическая задача. Перед выполнением этого задания учитель проводит с опорой на наглядность решение аналогичной ситуации.
Учитель берет непрозрачный пакет и на глазах детей кладет в него, например, 2 яблока и 3 груши (или любые другие предметы разной формы, которые легко узнать на ощупь).
Далее работа организуется так. Учащимся задаются вопросы:
– Сколько в пакете груш и яблок? (3 груши и 2 яблока.) Давайте подумаем, сколько раз можно вытащить по одному фрукту, чтобы обязательно достать грушу? Смотрите, я вытаскиваю один фрукт. (Рука учителя в пакете.) Обязательно ли это груша? (Нет, так как в пакете не только груши, но и 2 яблока.) (Учитель вытаскивает яблоко.) Действительно, в первый раз я могу вытащить не грушу, а яблоко. Сколько груш и яблок теперь осталось в пакете? (3 груши и 1 яблоко.) Вытаскиваю фрукт второй раз. Как вы думаете, это обязательно груша? (Нет, так как в пакете остались не только груши, но и 1 яблоко.) (Учитель опять вытаскивает яблоко.) Второй раз я снова могу вытащить яблоко. Сколько груш и яблок осталось в пакете? (3 груши и ни одного яблока.) Буду вытаскивать в третий раз. Как вы считаете, это обязательно груша? (Да, так как в пакете яблок больше нет.)
Делаем вывод: число возможных попыток у нас зависело не от числа груш, а от числа яблок.
Учитель убирает яблоки в пакет. Перед детьми ставится проблема:
– Сколько раз нужно вытащить по одному фрукту, чтобы обязательно достать яблоко? (Ученики быстро сообразят, что число попыток в этом случае зависит не от числа яблок, а уже от числа груш.) (Так как в пакете 3 груши, то мы можем гарантировать, что только в четвертый раз обязательно достанем яблоко.)
Теперь можно переходить к задаче, сформулированной в учебнике. Рассуждение аналогично.
Выводы:
1. Так как конфет «Смородина» – четыре, то надо взять не меньше пяти конфет, чтобы обязательно вытащить «Малину».
2. Так как конфет «Малина» – пять, то надо взять не меньше шести конфет, чтобы обязательно вытащить «Смородину».
2. Работа в печатной тетради № 1.
Задание № 85.
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите решение задачи по действиям.
Оформить решение задачи в тетради учащиеся должны следующим образом:
Решение:
1) 15 · 3 = 15 + 15 + 15 = 45 (гр.) – нашли.

2) 45 – 25 = (гр.) – пожарили.
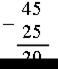
Ответ: 20 грибов.
При выполнении первого действия учащиеся используют фишки.
VI. Итог урока.
– Что нового узнали на уроке?
– Как выполнять сложение и вычитание двузначных чисел в столбик?
– Какие единицы длины вы знаете?
Домашнее задание: № 19 (учебник); № 80 (рабочая тетрадь).
Урок 27
Сложение двузначных чисел (общий случай)
Цели урока : рассмотреть общие приемы сложения двузначных чисел; совершенствовать навыки решения задач; развивать умение рассуждать и обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Чем похожи и чем отличаются друг от друга числа в каждой паре:
| 12 и 13 | 62 и 26 | 42 и 62 |
| 13 и 14 | 37 и 73 | 57 и 79 |
2. По какому правилу записан каждый ряд чисел:
а) 90, 60, 70, 40, 50, 20, 30, 0, 10;
б) 10, 30, 20, 40, 30, 50, 40, 60, 50.
3. Найдите значения выражений:
30 + 20 – 40 + 60 – 50 + 20 + 40 = 
80 – 30 – 10 + 50 – 70 + 60 – 80 = 
90 – 60 + 20 – 40 + 60 + 20 – 50 = 
30 + 40 – 60 + 80 – 20 – 60 + 10 = 
20 + 70 – 50 + 30 – 60 + 80 – 90 = 
4. Сколько отрезков с отмеченными концами можно найти на этом рисунке?
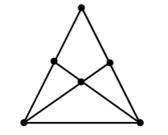
III. Сообщение темы урока.
– Сравните выражения каждого столбика:
| 25 + 12 | 25 + 19 |
| 46 + 24 | 46 + 25 |
– Чем отличаются выражения первого столбика от выражений второго столбика?
– Сегодня на уроке рассмотрим сложение двузначных чисел в пределах 100 с переходом через десяток.
Дата: 2018-12-28, просмотров: 673.