Подготовительные задания:
1) Назовите число, которое на 1 больше каждого из чисел:
6, 4, 8, 7, 0, 2, 9, 1, 5, 3.
2) Число 6 можно записать так: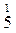 
. Какое число означает каждая из записей: 
?
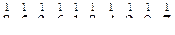Примечание.
Очень важно выработать у учащихся умение воспринимать подобные записи. Например, 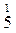как запись числа 6, являющегося суммой 5 и 1. Во-первых, это предупредит весьма распространенную ошибку, допускаемую детьми: в тех случаях, когда при сложении единиц в результате получается число, большее 10, они, сложив десятки, забывают прибавлять к ним еще 1 десяток. Во-вторых, представляется возможность сократить число шагов алгоритма сложения, что тоже немаловажно для выработки скорости вычислений.
Задание № 1 (с. 56).
– Рассмотрите рисунок на с. 56 и объясните, как Волк и Заяц выполняли сложение вида 27 + 15.
Один из учащихся рассказывает, что и как выполняют Волк и Заяц, а остальные дети работают параллельно, используя наборы оранжевых и белых палочек.
Задача: найти сумму 27 и 15.
Волк и Заяц составили «поезд» из 2 оранжевых и 7 белых «вагонов» и «поезд» из 1 оранжевого и 5 белых «вагонов». Затем к первому «поезду» они прицепляют слева один оранжевый, а справа – 5 белых «вагонов» из второго «поезда». Получился новый «поезд», в котором 3 оранжевых и 12 белых «вагонов». Но 12 – это 1 десяток и 2 единицы. Поэтому Волк и Заяц десяток белых «вагонов» заменили одним оранжевым «вагоном».
Длина «поезда» не изменилась. Получилось 4 оранжевых и 2 белых «вагона». Поезд обозначает число 42. Значит, сумма 27 и 15 равна 42.
Далее переходите к рассмотрению записи сложения этих чисел столбиком.
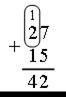
7 + 5 – двенадцать: 1 десяток (пишем маленькую цифру 1 над цифрой 2) и 2 единицы (пишем 2 под 5), 3 + 1 – четыре (пишем 4 под 1). Получается 42. В дальнейшем можно сократить рассуждение, сделать его более лаконичным.
Рассмотрите со всем классом следующие примеры:
Пример 1: сложить 64 и 29.
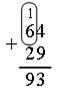
Объяснение: 4 + 9 – тринадцать: 1 десяток 3 единицы, 7 + 2 – девять. Сумма 93.
Пример 2: сложить 75 и 6.
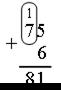
Объяснение: 5 + 6 – одиннадцать: 1 десяток 1 единица, 8 + 0 – восемь. Сумма 81.
Пример 3: сложить 4 и 58.
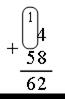
Объяснение: 4 + 8 – двенадцать: 1 десяток 2 единицы, 1 + 5 – шесть. Сумма 62.
Задание № 2 (с. 57).
Учащиеся работают в парах. Используя цветные палочки, они находят значение сумм с переходом через десяток.
Задание № 3 (с. 57).
Учащиеся выполняют задание с комментированием у доски, записывая сложение чисел в столбик.
V. Повторение пройденного материала.
1. Работа в печатной тетради № 1.
Задание № 85.
Если у учащихся нет возможности воспользоваться калькулятором, то выполнить проверку они смогут с помощью цветных палочек, что подготовит второклассников к изучению следующей темы.
Рассмотрим первый пример. Дети письменно выполняют вычисления и заполняют окошко.
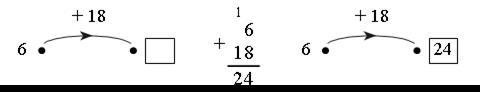
2. Работа по учебнику.
Задание № 10 (с. 58).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Все ли необходимые данные есть в тексте?
– Какие данные для решения задачи нужно взять из рисунка?
– Рассмотрите рисунок. Выполните схему к условию задачи.
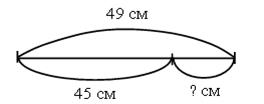
Решение:
49 – 45 = 4 (см).
Ответ: 4 см.
Задание № 11 (с. 58).
– Прочитайте задание.
– Какая команда одержала победу? (Команда «Вымпел».)
– Сколько очков составила разница в счете? Какое действие необходимо выполнить? (Вычитание, так как узнаем, на сколько больше очков у одной команды, чем у другой.)
Запись: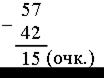 
Задание № 12 (с. 58).
– Рассмотрите рисунок. Какое действие надо выполнить, чтобы найти высоту второго этажа?
Запись: 4 м 69 см – 2 м 35 см = 2 м 34 см.
VI. Итог урока.
– Что нового узнали на уроке?
– Как выполнить сложение чисел с переходом через десяток?
– Что означает запись: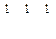 
?
Домашнее задание: № 8, 9 (учебник); № 83, 84 (рабочая тетрадь).
Урок 28
Сложение двузначных чисел (общий случай)
Цели урока : совершенствовать вычислительные навыки; продолжить формирование умений составлять задачи по иллюстрации и решать их; закреплять знания о многоугольниках; развивать умения анализировать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Работа с калькулятором.
– Наберите на калькуляторе любое двузначное число.
– Подумайте, на сколько можно его увеличить, чтобы изменялась только цифра, обозначающая десятки, а цифра, обозначающая единицы, не изменялась? Проверьте свои предположения на различных числах.
2. Задача.
– Чем похожи тексты задач? Чем отличаются? Какую задачу вы можете решить? Какую – нет?
– Почему?
| На одном проводе сидели ласточки, а на другом – 7 воробьев. Сколько всего птиц сидело на проводах? | На одном проводе сидело 9 ласточек, а на другом – 7 воробьев. Сколько всего птиц сидело на проводах? |
– Решите вторую задачу.
3. Какие числа нужно вставить в «окошки», чтобы получились верные равенства:
| 9 + 1 + = 14 | 9 + = 14 |
| 8 + 2 + = 17 | 8 + = 17 |
| 7 + 3 + = 13 | 7 + = 13 |
| 6 + 4 + = 12 | 6 + = 12 |
4. Сколько здесь треугольников?
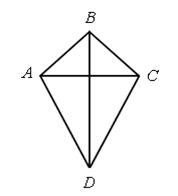
О т в е т: ∆АВС, ∆АВЕ, ∆ВСЕ, ∆ACD, ∆ADE, ∆CDE, ∆BCD, ∆ABD.
III. Сообщение темы урока.
– Сегодня мы продолжим закреплять навыки сложения двузначных чисел с переходом через десяток.
IV. Работа над темой урока.
Задание № 4 (с. 57).
– Прочитайте математические записи, используя выражения: «сумма чисел», «разность чисел», «уменьшить на», «увеличить на».
– Чем похожи все выражения? (В них есть скобки.)
– Какое действие выполняется первым в выражении со скобками?
– Проверьте, верно ли выполнены вычисления.
Запись:
(27 + 45) + 8 = 80 96 – (13 + 57) = 36 и т. д.
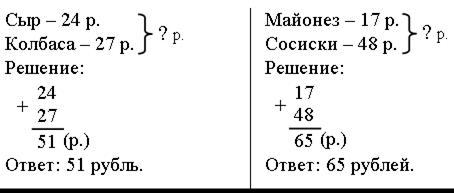
Задание № 5 (с. 57).
– Что необходимо знать, чтобы установить стоимость покупки?
– Все ли необходимые данные для этого содержатся в тексте?
– Запишите кратко условие задачи и решите ее по действиям.
Запись:
Дата: 2018-12-28, просмотров: 434.
