ОГЛАВЛЕНИЕ
Предисловие 
 Глава 1. Элементы теории множеств и математической логики
Глава 1. Элементы теории множеств и математической логики
51. Понятие множества
52. Способы задания множеств  .10
.10
53. Операции над множествами  12
12
54. Высказывания и операции над ними  17
17
55. Формулы логики высказываний  . 19
. 19
56. Булевы функции  20
20
57. Понятие об аксиоматической теории  23
23
58. Предикаты  30
30
Глава П. Соответствия, отображения (функции), бинарные отношения и операции  .37 51. Соответствие
.37 51. Соответствие  . 37
. 37
52. Отображение (функция)  38
38
53. Сужение отображения. График. Последовательность  . 39
. 39
54. Типы отображений  41
41
55. Композиция отображений, обратимые отображения  . 43
. 43
56. Бинарные и п-арные отношения  .48
.48
57. Операции над бинарными отношениями  . 51
. 51
58. Свойства бинарных отношений  . .53
. .53
59. Отношение порядка  55
55
510. Отношение эквивалентности  59 511. Операции на множестве
59 511. Операции на множестве  64 512. Понятие об алгебраической системе. Алгебрыи модели.
64 512. Понятие об алгебраической системе. Алгебрыи модели.
Классические примеры алгебр. Изоморфизм алгебр . 68
Глава Ш. Основы аксиоматической теории натуральных чисел  84 51. Аксиомы Пеано и следствия из них.
84 51. Аксиомы Пеано и следствия из них.
Первая форма метода математической индукции 84 52. Сложение и умножение натуральных чисел  . 89
. 89
53. Сравнение натуральных чисел  97
97
54. Ряд натуральных чисел и его свойства. Конечные множества  . 102
. 102
55. Вторая и третья формы метода математической индукции  .109
.109
Глава IV. Целые числа .  .112
.112
51. Кольцо целых чисел  112
112
52. Упорядоченность кольца целых чисел. Теоремы о наибольшем и наименьшем целом числе  121 53. Различные формы метода математической индукции для целых чисел. Теорема о делении с остатком .125 Литература
121 53. Различные формы метода математической индукции для целых чисел. Теорема о делении с остатком .125 Литература  131
131
ПРЕДИСЛОВИЕ
В основу учебного пособия положен курс лекций, апробированный на математическом факультете Волгоградского государственного педагогического университета.
” Вводный курс математики“ является необходимой составной частью учебного плана подготовки будущих учителей математики.
Основная задача состоит в построении общей терминологической базы, необходимой для постановки всех смежных математических дисциплин в педвузе.
В этом курсе заклаДывается фунДамент общеб математической культуры: вводятся основные понятия и вырабатывается язык, который в дальнейшем используется во всех математических дисциплинах на протяжении всего периода обУчения.
Пособие состоит из четырех глав. В первой главе рассматриваются операции над множествами, элементы исчисления высказываний и предикатов. Глава завершается понятием об аксиоматической теории.
Во второй главе изучаются соответствия, отображения, отношения, вводится понятие алгебраической системы и приводятся примеры основных классических алгебр (группоид, полугруппа, группа, кольцо и поле) 
В третьей главе строится эскиз аксиоматической теории натуральных чисел на базе аксиом Пеано, определяются операции сложения и умножения, вводится отношение порядка, изучаются свойства построенной системы. В ней также рассматривается связь между отрезками ряда натуральных чисел и конечными множествами. Глава завершается обоснованием различных форм метода математической индукции (для натуральных чисел).
Четвертая глава естественным образом продолжает третью. Здесь строится кольцо целых чисел, вводится понятие об упорядоченном кольце и изучаются свойства упорядоченности в кольце целых чисел, обобщаются различные формы метода математической индукции для целых чисел.
При написании данной книги автор хорошо осознавал, и в этом его убедила многолетняя практика, что этот курс нелегок для освоения студентами. Это объясняется в первую очередь наличием большого объема базовых понятий и, во-вторых, необходимостью его строгого изложения.
Поэтому автор стремился иллюстрировать понятия примерами, с этой же целью в книге приведено около ста упражнений для самостоятельного решения.
При построении аксиоматической теории натуральных чисел все доказательства проведены подробно, что в свою очередь может вызвать обратный эффект: некое утомление читателя. В этом случае читатель может опустить излишнюю на его взгляд детализацию.
Однако, по мнению автора, каждый математик и, в особенности, преподаватель математики должен хотя бы один раз в жизни детально познакомиться с доказательством основных утверждений о ” первичных“ объектах и отношениях, которые он постоянно использует в своей деятельности.
Пособие адресовано широкому кругу читателей и, в частности, студентам-заочникам. Его программа максимально приближена к школьному курсу математики. Разделы, которые непосредственно не изучаются в школе, могут составить основу факультативных курсов.
Г л а в а 
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И
Рис. 1
П р и м е р З. Множество R можно рассматривать как множество точек плоскости, лежащих между параллельными прямыми (рис. 2).

Рис. 2
У п р аж н е н и я:
1. Докажите равносильность следующих условий:
(Ь) Аи В = В
(с) Ап В = А.
2. Докажите, что если множество А состоит из п элементов, то множество Р (А) его подмножеств состоит из  элементов.
элементов.
3. Докажите: для любых множеств А, В, С
(а) если А С В , то А U С С В U С и А п С С В П С ; (Ь) если А С В , то А С С В Х С и С х В С С А .
4. Докажите равенства для любых множеств А, В, С :
ассоциативность операций объединения и пересечения) ;
(Ь) А ив = В U А, А В = В П А (коммутативность);
(d) А П (В U С) = (А 61 В) U (А П С) (дистрибутивность пересечения относительно объединения);
(е) А U (В П С) = (А U В) П (А и С) (дистрибутивность объединения относительно пересечения 
5. Используя свойства операций, сформулированные в упражнениях 1,4, докажите, что, если В С А, то

б. Докажите, что равенство А В = А справедливо тогда и только тогда, когда А П В О.
7. Докажите:

8. Докажите:
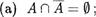
(Ь) если В С А, то А С В •
(с) (А) = А (закон инволюции);

(d) (А U В) = А П В и (А В) г: А U В (законы двойственности де Моргана) 
9. Включение А С В будем называть строгим, и множество А — правильной частью множества В , если ЩА 0 (т.е. существует элемент Ь ? В и Ь А).
Докажите, что если А С В и В С С, то множество А является правильной частью множества В тогда и только тогда, когда хотя бы одно из данных включений строгое.
В качестве примера докажем тождество
(А В) С (А П С) (В П С) (упражнение 7, пункт (а) ) 
Пусть с ? (А В) ПС. Тогда с ? А и с ? С, откуда, в силу определений разности и пересечения множеств, с ? А  с В и с ? С. Следовательно, с Е Ап С и с ? В П С и, значит, с (А ПС) (В П С) . Таким образом, (А В) С С
с В и с ? С. Следовательно, с Е Ап С и с ? В П С и, значит, с (А ПС) (В П С) . Таким образом, (А В) С С  (АОС) .
(АОС) .
Докажем обратное включение С пусть е . Тогда с ( АТС) и (ЮС) , откуда с А, с ? С и с В . Следовательно, ? А В и с е С . Это означает, что с ? (А В) С
 4. Высказывания и операции над ними
4. Высказывания и операции над ними
Высказыванием называется всякое предложение, относительно которого разумно говорить истинно тми ложно и которое не может быть оДновременно истинным и ложным.
П р и м е р. Высказываниями являются следующие предложения:
1) ” 5+3 равно 8” 
2) ” 14 делится на 3” 
З) ” Земля вращается вокруг Солнца“ 
4) ” 17 — простое число“ 
5) ” Уравнение с 2 +1 = О не имеет действительных корней“ . Высказывания 1,3,4,5 — истинны, а высказывание 2 — ложно. Логические операции. С помощью логических операций происходит построение нового, более сложного высказывания из некоторых исходных.
1. Отрицанием высказывания А называется высказывание —1,4 , которое истинно тогДа и только тогДа, когДа А ложно.
2.Дизъюнкцией высказываний А, В называется высказывание, которое истинно тогДа и только тогда, когДа истинно сотя бы одно из Данныс высказываний А либо В 
Дизъюнкция высказываний А, В обозначается через А Ч В и читается: А или В 
З.Конъюнкцией высказываний А, В называется высказывание А ЛВ (читается: ” А и В которое истинно тогДа и только тогДа, когДа истинны оДновременно оба высказывания А, В 
4. Импликацией от высказывания А к высказыванию В называется высказывание, которое ложно тогДа и только тогда, когДа А истинно, а В ложно. Это высказывание обоЗначается через А В и читается: ”если А , то В ” или ” А влечет В 
5. Эквиваленциеб двух высказываний А, В называется кОНЪЮНКЦИЯ (А В) л (В А) высказываний (А В) и (В А). Эквиваленция высказываний А, В обозначается
Таблицы истинности. Изучение свойств только что определенных операций во многих случаях удобно проводить с помощью таблиц истинности. Они возникают следующим образом: будем говорить, что высказывание А принимает значение истинности И, если оно истинно, и, соответственно, Л,
если оно ложно.
Таким образом, кажДому из высказываний будет приписан один из символов: И либо Л. При этом значение истинности сложного высказывания будет функцией от значений истинности составляющис его высказываний.
Эта функция определяется некоторой таблицей, которая позволяет вычислять значение истинности сложного высказывания в зависимости от значений истинности высказываний, из которых оно построено, с помощью логических операций.
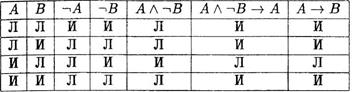
Например, операция отрицания может быть определена с помощью следующей таблицы истинности.
| и | л | ||
| л | и | ||
Ниже приводится сводная таблица истинности других логических операций: Дизъюнкции, конъюнкции, импликации и эквиваленции.
| А | в | АМВ | Ал В | ||||
| л | л | л | л | и | и | ||
| л | и | и | л | и | л | ||
| и | л | и | л | л | л | ||
| и | и | и | и | и | и | ||
Заметим , что логические операции отражают не связи межДу соДержанием высказываний, а зависимость значения истинности сложного высказывания от значений истинности составляющис его высказываний.
 5. Формулы логики высказываний
5. Формулы логики высказываний
Аналогично тому, как в алгебре с помощью арифметических операций строят сколь угодно сложные выражения из сиМВОЛОВ, обозначающих переменные величины, так и в логике определенные выше логические операции применяются Для построения из Данныс высказываний новыс, более сложныт. Ниже мы дадим определение формулы ЛоГИкИ высказываний. Буквы А, В, С . . . либо А; , Bi,Ci (i ? N) будут использованы для обозначения исходных или элементарных высказываний. Эти символы называются высказывательными переменными.
Понятие формулы логИКИ высказываний определяется следующими соглашениями:
1. Всякая высказывательная переменная есть формула.
2. Символы И и Л — формулы.
3. Если Ф — формула, то — формула.
4. Если Ф и — формулы, то (Ф Ч) , (Ф —» № ) , (Ф Л Ч)  (ф № ) — формулы.
(ф № ) — формулы.
5. Никаких других формул, кроме полученных в соотвеТствии с правилами 1 — 4, не существует.
Замечание. Это определение перечисляет правила построения новыс формул из любого множества исходных формул. Определения такого типа называются инДумпивными.
Так же, как в арифметике. скобки ( , ) служат Для указания послеДовательности Действий при построении формулы.
Для упрощения записи формул примем следующие соглашения об опускании скобок:
1. Будем говорить, что каждый из знаков в ряду Л, М,  4+ сильнее“ любого из знаков, следующих за ним в указанном порядке, т.е. отрицание сильнее“ конъюнкции Л , которая, в свою очередь, ” сильнее“ дизъюнкции и т.д.
4+ сильнее“ любого из знаков, следующих за ним в указанном порядке, т.е. отрицание сильнее“ конъюнкции Л , которая, в свою очередь, ” сильнее“ дизъюнкции и т.д.
2. Будем считать возможным опускать внешние скобки, например, вместо записи (Ф № ) писать Ф 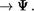
З. Остальные скобки опускаются таким образом, чтобы при их восстановлении из двух операций более ” сильная“ выполнялась раньше. В этом случае формула может быть названа по последней“ операции. Например, вместо записи 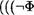 МУ) q) получим импликацию -лФ V q.
МУ) q) получим импликацию -лФ V q.
Булевы функции
Как уже отмечалось, строение формулы позволяет опреДелить ее значение истинности в зависимости от набора значений истинности элементарныс формул, из которых они построены (образованы). Это означает, что кажДая формула опреДеляет некоторую функцию, которая сама и ее аргументы принимают одно из значений И или Л.
Такие функции называются булевыми или функциями ал-
гебры ЛOГИћП.И.
Например, формулу А Л —тВ 'А можно рассматривать как выражение для функции Ф от переменных А, В , значения которой определяются следующими равенствами: Ф (Л,Л) 
 И, = И, = л и
И, = И, = л и 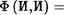 И.
И.
Формула Ф(А, В, . . . , С) логики высказываний называется тожДественно истинной или тавтологией, если она ПРИНИмает значение И при любом наборе значений истинности элементарных формул А, В, . . . , С , из которых она построена.
Например, тавтологиями являются следующие формулы

Формула Ф(А, В, . . . , С) называется тожДественно ложной, если она принимает значение Л при любом наборе значений истинности, составляющих ее элементарных формул А,В,. .. ,С.
Например, формула А Л ЗА тождественно ложна.
Равносильные формулы. Две формулы Ф(А, В, . . . , С) и Ч(А, В, . . . , С) называются равносильными, сли ОНИ опреДеляют одну и ту же булеву функцию. Запись Ф № означает равносильность формул.
Таким образом, Две формулы равносильны в том и только в том случае, если они принимают оДинаковые значения истинности при любом наборе значений истинности составляющис ис элементарныс формул.
Поэтому в равносильности двух формул можно убедиться сопоставлением их таблиц истинности.
Например, из таблицы истинности очевидным образом усматривается равносильность формул АЛ—В  А и А В.
А и А В.
Из определения непосредственно вытекает утверждение:  Две формулы Ф и № равносильны тогда и только тогда, когда их эквиваленция Ф является тавтологией. Другими словами, Ф тогДа и только тогДа, тсогДа Ф Е И“ .
Две формулы Ф и № равносильны тогда и только тогда, когда их эквиваленция Ф является тавтологией. Другими словами, Ф тогДа и только тогДа, тсогДа Ф Е И“ .
Равносильности формул играют важную роль в логических рассуждениях. Поэтому их часто называют законами логики. Приведем основные из них:
1. А —тА Е И (закон исключенного третьего).
П. А Л —1,4 Е- Л (закон противоречия)  Ш. —т—тА Е А (закон двойного отрицания)
Ш. —т—тА Е А (закон двойного отрицания)  IV. А Е А (закон тождества).
IV. А Е А (закон тождества).
V. А ч../ В В V А, А Л В В Л А (законы коммутативности). Ш. А А Е А, А л А Е- А (законы идемпотентности).
VII. (В С) Е- (А V В) мс, Ал (В л С) Е (А Л В) Л С законы ассоциативности 
VIII. АЛ (В V С) Е (Ал В) ч./ (А Л С) (закон дистрибутивности конъюнкции относительно дизъюнкции). IX. А V (В Л С) (А В) Л (А V С) (закон дистрибутивности дизъюнкции относительно конъюнкции).
Х. А Л (А В) —+ В -Е И ( закон отделения 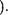
 (А
(А  В) Л (В С) (А С) И (закон СИЛЛОГИЗМа).
В) Л (В С) (А С) И (закон СИЛЛОГИЗМа).
ХИ. А  В Е —1,4 V В (закон исключения импликации).
В Е —1,4 V В (закон исключения импликации). 
XIII. А  В
В  -м4 В (закон исключения дизъюнкции). ХУ.
-м4 В (закон исключения дизъюнкции). ХУ.  —АЛ—В,
—АЛ—В, 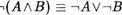 (законы де Моргана
(законы де Моргана 
ХУ. А  В
В  --;В —1,4 (закон контрапозиции).
--;В —1,4 (закон контрапозиции).
Убедиться в справедливости каждой из перечисленных вы-
Ше равносильностей можно, например, с помощью сопоставления таблиц истинности для формул, стоящих в левой и правой частях каждой из них.
Этого можно добиться, не прибегая к таблицам истинности. В качестве примера докажем равносильность формул
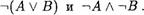
Допустим, что формула —т(А 'V В) принимает значение И, тогда формула А В принимает значение Л. Это означает, что каждая из формул А и В принимает значение Л, откуда следует, что формулы —тА и —тВ одновременно принимают значение И, т.е. —тА Л -лВ принимает значение И.
Пусть 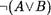 принимает значение Л. Тогда А мВ имеет значение И. Это означает, что хотя бы одна из формул А или В принимает значение И, откуда в свою очередь следует, что хотя бы одна из формул —и4 , —тВ имеет значение Л и, следовательно, —и4 Л —-лВ принимает значение Л. Таким образом, АА V В) —тА Л -лВ .
принимает значение Л. Тогда А мВ имеет значение И. Это означает, что хотя бы одна из формул А или В принимает значение И, откуда в свою очередь следует, что хотя бы одна из формул —и4 , —тВ имеет значение Л и, следовательно, —и4 Л —-лВ принимает значение Л. Таким образом, АА V В) —тА Л -лВ .
Логическое следствие. Пусть Ф(А1 , 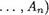 и Ч(А1, , Ап) — две формулы логики высказываний, построенные из элементарных формул 341, .
и Ч(А1, , Ап) — две формулы логики высказываний, построенные из элементарных формул 341, . 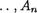
Будем говорить, что формула № (А  А
А  , , Ап) является ЛОГИЧеСКИ.М слеДствием формулы Ф(А А
, , Ап) является ЛОГИЧеСКИ.М слеДствием формулы Ф(А А  , Ап), что записывается так:
, Ап), что записывается так:
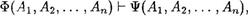
если формула принимает значение И при всес наборас значений истинности элементарных формул „41 , „42, . , Ап , при которых формула Ф истинна. Формула Ф при этом называется посылкой, а № — заключением.
Из определения непосредственно вытекает: Ф Ф тогда и только тогда, когда
ф — тавтология (1)
Например, А А В, А Л В У— А для любых формул
А и В .
Определение логического следствия можно распространить на любое количество посылок следующим образом:
“ Формула № называется логическим слеДствием формул 91, • • . , рп, если № принимает значение И во всес случаяс, когда формулы 91, . . . , истинны. Запись 91, . . , рп н ч будет обозначать, что формула является логическим следствием формул 91, . 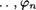
Непосредственным образом проверяется справедливость следующего утверждения 91, . . . , ро Ё— тогДа и только тогДа, тсогДа
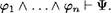 (2)
(2)
Г л ав а П
Последовательность
Пусть имеем отображение .f : Х У, и пусть (7 С Х 
Тогда отображение f всякому элементу из G ставит в соответствие некоторый элемент из У , стало быть, оно определяет отображение fG : G У .
Отображение fG в этом случае называют сужением отображения f на множество (7 (рис. 4).

Рис. 4
П р и м е р 1. Отображение f(c) = 2 3 , определенное для ? Z, есть сужение на Z отображения f(c) — — сз множества
Множество пар {с, f(c)}, являющееся подмножеством проИзведения Х ХУ, называется графиком функции f(c) (рис. 5).

Рис. 5
П р и м е р 2. Множество пар {с, 22 } являющееся подмножеством произведения R2 = R х R , составляет график показательной функции f(c) 2с (рис. 6).
2

| |
| О | х |
Рис. 6
Возьмем N— множество натуральных чисел, в качестве У — произвольное множество.
Отображение f : N У называется последовательностью элементов из У .
Таким образом, последовательность f связывает каждое натуральное число п с некоторым элементом Л) из У 
Последовательность .f будем обозначать f = {f1, .f2' • • • 
 или сокращенно .f = {fn} . Здесь символы Л являются образами чисел из N. Например, запись f = {щ} означает последовательность рациональных чисел вида {1, 12 ,
или сокращенно .f = {fn} . Здесь символы Л являются образами чисел из N. Например, запись f = {щ} означает последовательность рациональных чисел вида {1, 12 , 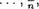 1
1
 4. Типы отображений
4. Типы отображений
Пусть f : Х У — отображение. Тогда каждому элементу с е Х соответствует единственный элемент у У , с другой стороны, элемент у е У может быть образом нескольких элементов из Х .
Например, значение —6 служит для функции у г: с 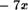 образом значений —3, 1, 2. Множество элементов с Х , имеюших в качестве образа при отображении f один и тот же элемент у ? У , называется множеством прообразов элемента у и обозначается f-1 (y) •
образом значений —3, 1, 2. Множество элементов с Х , имеюших в качестве образа при отображении f один и тот же элемент у ? У , называется множеством прообразов элемента у и обозначается f-1 (y) •
Пусть 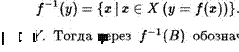 (В) обозначается множество всех прообразов элементов, принадлежащих множеству В ,
(В) обозначается множество всех прообразов элементов, принадлежащих множеству В ,
т.е.
f -1 (B) = Х, f(c) е Щ.
 1. Отображение f : Х У называется сюръективным, или сюръекцией, или отображением на множество У , если каждый элемент у ? У из области его значений имеет хотя. бы один прообраз, т.е. множество не пусто для всякого элемента у е У.
1. Отображение f : Х У называется сюръективным, или сюръекцией, или отображением на множество У , если каждый элемент у ? У из области его значений имеет хотя. бы один прообраз, т.е. множество не пусто для всякого элемента у е У.
Очевидно, что отображение' f : Х У является сюръекцией тогда и только тогда, когда ЛХ) = У . Заметим, что в этом утверждении равенство ЛХ) = У можно заменить равносильным ему равенством: (У) = Х.
а) Пусть Х = У R . Отображение f , определяемое формулой f(c) = 52 + 1 , задает сюръективное отображение множества Х на множество У.
б) Пусть Х У R . Отображение f, определяемое формулой f(c) сз , есть отображение R на R , поскольку любое действительное число является кубом некоторого действительного числа. Напротив, если Х = У Z , то отображение 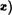 — сз множества Z в Z уже не будет сюръекцией, поскольку целое число может не быть кубом целого числа. Например, (2) О
— сз множества Z в Z уже не будет сюръекцией, поскольку целое число может не быть кубом целого числа. Например, (2) О 
в) Пусть снова Х У = R . Отображение f, определяемое формулой f(c) — 2 2 , есть отображение в У . Это отображение не сюръективно, т.к. отрицательные числа из У не имеют прообразов при отображении f.
2. Говорят, что отображение f : Х —; У является взаимнооднозначным или инъективным, если образы любых двух различных элементов с1, ? Х различны, т.е. из неравенства ст 22 вытекает f(C1) f(C2) .
З. Отображение f : Х У называют биективным или биекцией, если оно оДноеременно инъективно и сюръективно, т.е. если каждый элемент У является образом некоторого единственного элемента из Х.
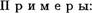
Отображение, заданное на рисунках:
 — сюръективно, но не инъективно; инъективно, но не является сюръекцией; биекция; не обладает ни одниМ из указанных свойств.
— сюръективно, но не инъективно; инъективно, но не является сюръекцией; биекция; не обладает ни одниМ из указанных свойств.




 о
о 
а) 6)в)г)
Рис. 7
Отображение f : Х У, определенное равенством f(c) =  с, называется тожДественным, и обозначается: 1х : Х —»
с, называется тожДественным, и обозначается: 1х : Х —»
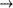 Х . Если Х С У , то отображение f : Х —» У, определенное равенством f(c) с, называют тсаноничестсой инъекцией.
Х . Если Х С У , то отображение f : Х —» У, определенное равенством f(c) с, называют тсаноничестсой инъекцией.
 5. Композиция отображений, обратимые отображения
5. Композиция отображений, обратимые отображения
Пусть Х, У, 7— множества f : Х У и : У —» 7, — отображения. Отображение h : Х 7), определяемое формулой 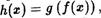 называется композицией, или суперпозицией, или произв еДением отображений f и g и обозначается через go f
называется композицией, или суперпозицией, или произв еДением отображений f и g и обозначается через go f 
В том случае, когда f и g именуются функциями, g о f называется сложной функцией.
Теорема 1. Композиция отображениб облаДает слеЭуюЩИ.ИИ свойствами:
1) если f : Х У , g : У —4 Z и h : Z ил — отображениз, то (hog) of = Но (go f) (ассоциативность композиции);
2) Для любого отображения : Х —» У имеют место равенства f о 1х f и 1у о f Л
пусть f : Х У, : У а : Z ил, т.е. X4y4Z3W, то (go f).
Действительно, для любого ? Х имеем:
((hog) о f) (с) = (h о 9) (f(c)) = h(g (f(c)))
т.е. (ф og) о Л (с) — и значит (h о g) о f 
Пусть f : Х У— отображение. Тогда е Х (f о = = f(c) , т.е. fo 1х = f.
Аналогично доказывается равенство 1у о f = f.
Замечание. Композиция отображений в общем случае не обладает коммутативностью, существуют отображения f и р , что произведения f о р и р о f одновременно определены, но не равны между собой, f о р 74 р о Л
Например, пусть f : R R , f(c) 2 2 , 9 : R R, 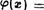 sinc . Тогда (р о = — sin . С другой стороны, (f о sin2 с. Очевидно, что sinc 2 и sin2 с— различные функции, т.е. р о .f f о р.
sinc . Тогда (р о = — sin . С другой стороны, (f о sin2 с. Очевидно, что sinc 2 и sin2 с— различные функции, т.е. р о .f f о р.
Отображение .f : А В называется обратимым, если
существует отображение р : В А такое, что
pof= 1 А и Г о р = 1в.
Отображение р , удовлетворяющее равенства (*), называется обратным к отображению 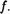
Критерием обратимости отображения служит теорема 2.
Теорема 2. Отображение обратимо тогДа и только тогДа, когДа оно биективно.
Н е о б х о д и м о с т ь. Пусть f : А В— обратимое отображение. Тогда, по определению, существует отображение р : В А такое, что выполняются оба равенства 
Покажем, что отображение f сюръекчпивно. Пусть Ь ? В. Тогда, используя равенство р о f = 1 в, получим f (p(b)) = 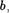 откуда следует, что p(b) — прообраз элемента Ь при отображении f . Следовательно, f— сюръективно.
откуда следует, что p(b) — прообраз элемента Ь при отображении f . Следовательно, f— сюръективно.
Докажем инъективность отображения f. Пусть с1, 22 ? ? А и 74 22 . Допустим, что f(C1) f(C2) . Тогда р (f(Z'l)) = , т.е. (ро ) = (ро Поскольку р о f 1 А, то предыдущее равенство может быть записано в виде 1А(С1) 1А(С2), т.е. 21 что противоречит предположению. Поэтому f(C1) 74 f(Z2) и, следовательно, f— инъективно. Таким образом, f— биекция.
Д о с т а т о ч н о с т ь. Пусть f : А В— биективное отображение. Тогда ввиду сюръективнос.ти отображения 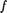
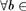 В (f -1 (b) О)
В (f -1 (b) О) 
В силу инъективности f для любого элемента Ь ? В множество Г 1 (Ь) не может содержать более одного элемента и. следовательно, оно одноэлементно.
В силу этого в дальнейшем Для любого биективного отображения f под символом (Ь) условимся понимать не множество, а элемент, из которого состоит это множество.
Тогда соответствие р из В в А, при котором образом произвольного элемента Ь е А является элемент (Ь) ? А  есть отображение.
есть отображение.
Теперь для доказательства обратимости отображения f достаточно проверить справедливость равенств 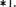
1. Пусть а А . Тогда
(ро = р (f(a)) (f(a)) 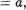
т.е. pof= 1 А .
2. Далее, пусть Ь В . Тогда, по определению, p(b) 
 , откуда f (p(b)) f (f -1 (b)) — Ь. Следовательно, f о р = 1 в . Таким образом, f — обратимо.
, откуда f (p(b)) f (f -1 (b)) — Ь. Следовательно, f о р = 1 в . Таким образом, f — обратимо.
Теорема доказана.
Следствие. Если отображение f : А В обратимо, то оно имеет еДинственное обратное тс нему отображение.
Д о к а з а т е л ь с т в о. Пусть отображение f : А —4 В— обратимо. Тогда, в силу теоремы 2, отображение f— биективно. Обозначим через : В А отображение, обратное к f, построенное в доказательстве теоремы 2, т.е. 91 (Ь) = (Ь) для любого Ь ? В.
Пусть 92 : В А — произвольное отображение, обратное к f . Тогда 910f = 1 А, f0P1 1 в и = 1 А, f0P2 = 1 в.
Используя эти равенства и ассоциативность композиции отображений (теорема 1), получим
92(Ь) = (92 о = (92 о (f о 91) ) (Ь) = ((92 о f) о (ь) =  (1А о г: 91 (Ь) для произвольного Ь ? В
(1А о г: 91 (Ь) для произвольного Ь ? В 
Таким образом, 92 . Следствие доказано.
Это следствие дает основание ввести станДартное обозначение отображения, обратного к данному:
если f биективно, то через обозначается отображение, обратное к f .
Напомним, что для любого элемента Ь ? В, по определению, 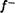 (Ь) — есть прообраз Ь при отображении f.
(Ь) — есть прообраз Ь при отображении f.
Таким образом, равенства
.f —1 1 А fof 1в являются определяющими для отображения —1 
У п р а ж н е н и я:
1. Пусть f : Х У — отображение. Докажите справедливость следующих импликаций:
(а) А С В ЛА) С Л В) для любых подмножеств А и В множества Х 
(Ь) С С D (С) С для любых подмножеств С и D множества У.
2. Пусть f : Х У — отображение, А и В- произвольные подмножества множества Х. Докажите справедливость следующих соотношений:
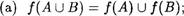
ф) ЛА п В) = ЛА) п ЛВ); (с) ЛА) ЛА \ В).
З. f : Х —» У— инъекция, А С В С Х. Докажите, что
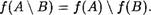
4. Пусть f : Х У — отображение, С и D— произвольные  подмножества множества У. Докажите справедливость следующих равенств:
подмножества множества У. Докажите справедливость следующих равенств:
(а) f-1 (C u D) f -1 (D); ф) f-1 (C f -i (C) f -l (D); (с) f-1 (C) \ f-1 (D).
5. Пусть f : А В— отображение. Доказать равносиль  ность следующих утверждений:
ность следующих утверждений:
(а) f— сюръективно;

(с) и ? в (f-1 (b) 0) .
6. пусть fi : R + R, : R — R (i — 1, 2, З) и для любого
Л (с) Зс + 1, 91 (с) = 22 3  f2(c) 2с — 1, Р2(с) —
f2(c) 2с — 1, Р2(с) —  f3(c) = 5, рз(с) = tgc
f3(c) = 5, рз(с) = tgc 
Найти композиции Л о pt• и р; о Л 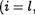
7. 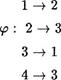 Пусть А =
Пусть А = 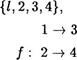
Построить р о .f и f о р .
8. Пусть f : А В— отображение. Докажите, что f является биекцией тогда и только тогда, когда множество 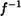 (Ь) одноэлементно для любого Ь е В.
(Ь) одноэлементно для любого Ь е В.
9. Докажите, что отображение f : А В инъективно тогда и только тогда, когда для любого элемента, Ь ? В множество (Ь) либо пусто, либо одноэлементно.
10. Какие из отображений, указанных в упражнении 6, сюръективны, инъективны, биективны?
11. Докажите, что всякая возрастающая (убывающая) функция действительного переменного является инъекцией.
12. Два отображения называются однотипными, если оба они одновременно инъективны, сюръективны, либо биектив-
Докажите, что композиция двух однотипных отображений является отображением того же типа.
13. Докажите, что если отображение f обратимо, то обратное к нему отображение биективно и имеет место равенство (f ) 1 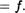
14. Докажите, что если композиция fop инъективна (сюръективна), то один из сомножителей f либо р также инъективен (сюръективен).
15. Пусть f и g— обратимые отображения. Докажите, что если их композиция f о g существует, то (f о g)—1 
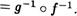
 6. Бинарные и п -арные отношения
6. Бинарные и п -арные отношения
В математике мы часто используем термины, которые характеризуют некоторые связи межау парами объектов в опреДеленном поряДке. Например, ” меньше“ включается“ , ” делится на параллельно“ и т. д. Ниже мы увидим, что каждый из этих терминов является конкретизацией более широкого — бинарное отношение 
Для того, чтобы увидеть подходы к определению этого понятия, обратимся сначала к примеру.
Пусть А {1, 2, 6} . Тогда свойство ” меньше“ выДеляет в Декартовом кваДрате „42 подмножество S = {(1, 2), (1, 6),  состоящее из тех и только тех пар чисел, у которых первое число меньше второго. Аналогично подмножество
состоящее из тех и только тех пар чисел, у которых первое число меньше второго. Аналогично подмножество

сарактеризует свойство “Делимости” чисел на множестве А А именно, число с Делит у тогДа и только тогДа, когДа

Таким образом, если множество F известно заранее, то для положительного ответа на вопрос ” является ли число а делителем Ь ?” достаточно убедиться в том, что (а, Ь) ( 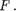 Этим рассуждением мы вплотную приблизились к понятию бинарного отношения.
Этим рассуждением мы вплотную приблизились к понятию бинарного отношения.
Определение. Любое подмножество S С „4 2 Декартова кваДрата множества А называется бинарным отношением, опреДеленным на множестве А .
Из определения соответствия вытекает, что бинарное отношение на множестве А может быть опреДелено как соответствие из А в А.
Если пара (с, у) ? S , где с, у (- А , то говорят, что элементы с и у находятся в отношении S . Вместо записи (с, у) ? S используется также cSy или S(c, у) 
Отметим некоторые наиболее распространенные способы заДания бинарныс отношений:
1) Бинарное отношение может быть задано перечислением его элементов.
Например, как уже отмечалось, множество , заданное равенством , определяет бинарное отношение делимости“ на множестве А = {1 , 2, 6} 
2) Бинарное отношение можно рассматривать как область истинности Двухместного преДиката.
Например, отношение 17 , о котором говорится в пункте 1)  совпадает с областью истинности предиката
совпадает с областью истинности предиката
 ” с делит
” с делит 
З) Бинарное отношение как частный случат) соответствия может быть заДано с помощью стрелок .
Например, отношение F , определенное равенством 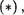 может быть задано следующим образом:
может быть задано следующим образом:
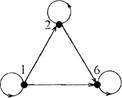
Рис. 8
Такой рисунок часто называют Диаграммой или графом отношения F .
Диаграмма бинарного отношения 17 состоит из точек, изображающих основное множество А и стрелок, соеДиняЮ?.цис ис. При этом стрелка с началом с и концом у присутствует в диаграмме тогда и только тогда, когда (с, у) F  Диаграмма чаще всего используется для задания бинарных отношений на конечных множествах.
Диаграмма чаще всего используется для задания бинарных отношений на конечных множествах.
4) В случае, когда бинарное отношение задается на множестве действительных чисел R , множество принадлежащих ему пар может быть изображено точками плоскости. Это дает геометрическую иллюстрацию соответствующего отношения.Напримео, множество пар (с, у), для которых выполняется отношение с > у, представляет множество точек плоскости, лежащих под прямой у = (см. рис. 9).
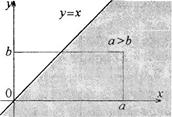
Рис. 9
Подмножество Д С Х х Х, составленное из всех пар равных между собой элементов, называется Диагональю множества Х х х, т.е.
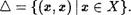
Из определения вытекает, что отношение S(c, с), определяемое множеством Д, является равенством.
В предыдущем примере (рис. 9) диагональю Д множества S х S будет множество точек прямой у = с.
Заметим, что понятие бинарного отношения может быть распространено на более общую ситуацию. Для этого достаточно в определении бинарного отношения заменить слова ” декартов квадрат“ словами ” декартова степень 
Определение. Пусть А — множество и п — произвольное натуральное число. ТогДа любое подмножество S С АП Декартовой степени множества А с показателем п называется п -арным отношением на множестве А .
В частности, при п = 2 получаем определение бинарного отношения. При п = 1 отношение называется унарным.
Отметим далее, что в математических рассуждениях слова п -арное отношение и п -местный преДикат часто используются как СИНОНИМЫ.
Проиллюстрируем эту связь для случая п = 2 
Как мы уже отмечали, область истинности любого Двусместного преДитсата Р(с, у) является бинарным отношением. Обратно, если S — бинарное отношение на множестве А,
т. е. S С А х А, то, определив Р(с, у) как предложение “пара (с, у) принадлежит множеству S “, мы получим предикат, обласТЬ истинности которого совпадает с исходным бинарным отношением S .
Таким образом, называя бинарное отношение преДикатом, мы поДразумеваем при этом Двусместный преДикат, областью истинности которого является Данное отношение. Это соглашение относится и к произвольным п -арным отношеНИМ.
Рис. 11
Отношение называется транзитив ным, если из того, что (с, у) ? F и (у, 2) F следует, что пара (с, z) е F для любых элементов г, y,z ? А, или
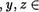 А (zFy Л yFz cFz).
А (zFy Л yFz cFz).
Например, отношение ” больше“ для действительных чисел транзитивно: если с > у и у > z , то и с z.
Отношение называется антисимметричным, если  того, что (с, у) ? и (у, с) ? F следует, что с = у , т.е.
того, что (с, у) ? и (у, с) ? F следует, что с = у , т.е. 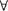 с, у ? А (cFy Л yFz с = у).
с, у ? А (cFy Л yFz с = у).
Следующее предложение показывает, что каждое из определенных выше свойств бинарных отношений равносильно некоторому свойству операций над этими отношениями.
Предложение. Пусть F — произвольное бинарное отношение на некотором множестве А .
ТогДа:
1) Р— рефлексивно  Д С , где Д — диагональ на множестве А ;
Д С , где Д — диагональ на множестве А ;
2) 17 — симметрично 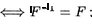
З) Р— транзитивно  FoF С F
FoF С F 
2) Р— антисимметрично F П  С д .
С д .
Докажем, например, утверждение 2) 
Пусть F симметрично на множестве А и (г, у) (- F—1  Тогда (у, с) F , откуда в силу симметричности отношения F следует, что (с, у) ?- F , и, значит, С F .
Тогда (у, с) F , откуда в силу симметричности отношения F следует, что (с, у) ?- F , и, значит, С F .  Докажем обратное включение.
Докажем обратное включение.
Пусть (с, у) Р. Отсюда в силу симметричности отношения F следует, что (у, с) ? Е, откуда, по определению, (с, у) е Р—1. Следовательно, F С Таким образом,

Этим доказана импликация
— СИЛЬКТРИЧНО 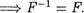
Докажем обратную импликацию.
Пусть = и (г, у) F для некоторой пары (с, у) е А х А. Тогда в силу равенства Е-1 = F получим, что (с, у) е откуда, по определению, следует (у, г) ? Р. Таким образом,

для любой пары (с, у) ? А У. А и, значит, Е— симметрично.
Отношение порядка
Рефлексивное, транзитивное и антисимметричное бинарное отношение называется отношением частичного поряДка.
Легкб видеть, что известное отношение < меньше либо равно") является отношением частичного порядка на любом множестве чисел.
Другим классическим примером этого типа отношений является отношение С включения“ на множестве Р (А) всех подмножеств произвольного фиксированного множества А.
Бинарное отношение на множестве А называется отношением строгого поряДка, если оно антирефлексивно ((а, а) Р для любого а Е А), транзитивно и удовлетворяет дополнительному условию
У а, Ь е А (aFbv bFa).
Например, отношение ” меньше“ на множестве действительных чисел является отношением строгого порядка.
В дальнейшем для обозначения отношения частичного порядка на произвольном множестве А , как правило, будет использоваться стандартный знак < .
Фраза: (А, — частично упорядоченное множество“ озна-
чает, что на множестве А задано отношение частичного порядка < .
Вместо слов ”частично упорядоченное множество“ используется также сокращенная запись ч.у. множество 
Пусть (А, — ч.у. множество. Элементы а, Ь А называются сравнимы.ИИ, если выполняется хотя бы одно из условий a < b либо Ь 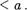
Частично упорядоченное множество, в котором любые Деа элемента сравнимы, называется линейно упоряДоченным или цепью.
Пусть (А, — ч.у. множество. На множестве А зададим новое бинарное отношение > по правилу:
Уа, Ь 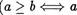 < Ь).
< Ь).
Очевидно, что отношение > также является отношени  ем частичного порядка. Этот порядок называется двойственвым к данному.
ем частичного порядка. Этот порядок называется двойственвым к данному.
Заметим, что если взять порядок, двойственный к > , то получим исходный порядок < .
Ч.у. множество (А, >) называется Двойственным к ч.  множеству (А,
множеству (А, 
Пусть Ф — некоторое утверждение о ч.у. множествах, сформулированное в общелогических терминах (и терминах отношения частичного порядка).
Утверждение Ф * , полученное из Ф заменой всес всожДениб знака < на знак Двойственного тс нему отношения, называется утеержДением, двойственным к Ф.
В теории ч.у. множеств имеет место интересный факт, относящийся к теоремам этой теории.
Принцип двойственности. Если некоторое утвержДение Ф верно для всех упоряДоченныс множеств (т.е. является теоремой теории ч.у, множеств), то Двойственное тс нему утвержДение также верно Для всес ч.у. множеств.
Подчеркнем еще раз значение слова ”Для всес" в формулировке принципа Двойственности. Если какое-либо утверждение верно для конкретного ч.у. множества, то этот факт совсем не означает, что и двойственное утверждение будет верным Р этом частично упорядоченном множестве.
Принцип двойственности позволяет ” экономить на доказательствах" (избавляет от проведения лишней работы).
Справедливость его имеет место в силу того, что утверж-
Дение Ф верно в ч.у. множестве (А, тогДа и только тогДа, когда Двойственное тс нему утвержДение Ф* имеет место в ч.у. множестве (А, .
Таким образом, принцип двойственности является непосредственным слеДствием опреДелений двойственного порядка и двойственного ч.у. множества.
Однако для сомневающегося читателя мы можем предложить следующую стаму рассужДений для обоснования этого
принципа.
Пусть Ф— утверждение, о котором говорится выше. Его можно представить в виде импликации Р S двух предложений ( Р— посылка, S — заключение утверждения Ф )  Тогда утверждение Ф * будет выглядеть так:
Тогда утверждение Ф * будет выглядеть так:
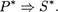
Пусть теперь утверждение Ф верно в любом частично упоряДоченном множестве.
Пусть (А, — произвольное частично упорядоченное множество. Покажем, что Ф * верно в А . Для этого нужно убедиться в том, что утверждение S* является следствием утверждения Р* (об элементах множества А). Применим метод вспомогательной гипотезы. Предположим, что Р* верно в (А, . Тогда (Р*)* верно в двойственном ч.у. множестве
Далее, очевидно, что (Р*)* = Р, т.е. Р верно в (А, . Отсюда, поскольку импликация Р S верна в любом ч.у. множестве, то S верно в КА, >) , откуда следует, что S* верно в двойственном ч.у. множестве (А, 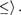
Таким образом, из предположения справедливости Р* в КА, следует справедливость S * в (А, и, значит, утверждение Р S * верно в КА, , т.е. Ф * верно в (А, <) .
Ниже будут приведены примеры применения принципа двойственности.
Пусть (А, — произвольное ч.у. множество.
Элемент а ? А называется минимальным, если из с < а слеДует с а Для любого ? А .
Двойственным образом получаем определение максимального элемента:
Элемент а называется максимальным, если из с > а слеДует с = а Для любого с ? А 
Это означает, что при построении предложения Ф * , двойственного к Ф, необходимо заменить на всех местах слово ” минимальный” на ” максимальный“ и обратно.
Элемент а называется наи.,иеньшим, если а < с Для всес
Двойственное понятие:
Элемент а называется наибольшим, если а > с Для всес
Пр им е р ы:
1. Очевидно, что ВсякиЙ наименьший элемент является МИНИЛшЛЬНЫМ. По принципу двойственности отсюда следятет, что всякий наибольший элемент является максимальным.
2. Покажем, что если в ч. у. множестве (А, существует НОИЛсНЬШИЙ элемент а , то он единственен. При этом во множестве А никаких других наименьших элементов, отличных от а, не существует.
Действительно, пусть а— наименьший элемент в А .
Предположим, что Ь также является натьиеньшил в А  Тогда, с одной стороны, а < Ь , поскольку а— наименьший в А , а с другой — Ь < а . Отсюда в силу свойства антисимметричности отношения < следует, что а = Ь
Тогда, с одной стороны, а < Ь , поскольку а— наименьший в А , а с другой — Ь < а . Отсюда в силу свойства антисимметричности отношения < следует, что а = Ь 
Далее, пусть с— произвольный минимальный элемент в А  Тогда а < с , поскольку а— наименьший, откуда в силу определения минимального элемента получим, что а = с .
Тогда а < с , поскольку а— наименьший, откуда в силу определения минимального элемента получим, что а = с .
Отсюда по принципу Двойственности справедливо следукощее предложение: “Если ч.у. множество (А, соДержитп наибольший элемент, то кроме него во множестве А никакис ни НСИб0ЛЬШИС, ни максимальныс элементов не существует 
Предлагаем читателю в качестве интересного упражнения
получить текст доказательства этого утверждения из доказательства предыдущего утверждения, заменив в нем каждую фразу двойственной.
Отношение эквивалентности
Наряду с отношениями порядка в математике особую роль играют бинарные отношения, которые одновременно обладают свойствами рефлексивности, симметричности и транзитивности. Любое такое отношение принято называть отношением эквивалентностпи или эквивалентностью на данном множестве.
Для обозначения эквивалентности используется, как правило, станДартньиЈ знак . Например, запись у означает, что с находится в данном отношении с у .
Простейшим примером отношения эквивалентности на множестве Х может служить отношение равенства между элементами этого множества.
Укажем примеры отношений эквивалентности, которые не являются равенством.
П р и м е р 1. Пусть т Z и т > 1 . (Z— множество всех целых чисел). Определим бинарное отношение F на множестве Z как область истинности предиката Р(с, у) .

г — у делится на т“ 
Это означает, что
сру ВК ? — у = Кт) либо в краткой записи
zFy (с — у) : т.
Покажем,что F — эквивалентность на множестве Z 
1. Рефлексивность ОТНОШениЯ F 
 Поскольку 0 : т, то (с — с) : тп для любого числа с (- Z откуда следует, что
Поскольку 0 : т, то (с — с) : тп для любого числа с (- Z откуда следует, что
Vc(cFc).
2. Симметричность отношения F 
Пусть cFy для некоторых чисел с, у ? Z . Тогда существует число К ?- Z такое, что Кт , откуда = (—К)т,
т. е. (у — с) : т, и, значит, yFz .
З. Транзитивность отношения F .
Пусть сру и yFz для некоторых чисел с, Z . Тогда с — у = k1rn и 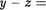 к2т, где К1, К2 ? Z
к2т, где К1, К2 ? Z 
Отсюда получаем
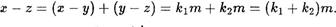
Следовательно, (с — z) : т и, значит, cFz .
П р и м е р 2. Пусть А, В— множества и f : А В  отображение. Определим на множестве А бинарное отношение S по правилу
отображение. Определим на множестве А бинарное отношение S по правилу
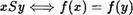
для любых элементов с, у ? А .
Простая проверка показывает, что S — эквивалентность на множестве А 
Это отношение называют ядром отображения 
Свойства бинарной операции
Ассоциативность. Бинарная операция Т называется ассоциативной, если аТ ФТС) = (атьрс для любых элементов а, Ь, с ? А 
Например, сложение и умножение во множестве натуральных чисел N ассоциативно, а возведение в степень — не ассоциативно, поскольку равенство (а ) = ab выполняется не для всех натуральных чисел. Например, (22 ) 3 223 
Коммутативность. Бинарная операция Т называется коммутативной, если аТЬ = ЬТа для любых а, Ь ? А .
Регулярный элемент. Элемент а называется регулярным относительно бинарной операции Т , если для любых с, у ? А, равенства аТс ату и гТа = ута влекут с = у . В этом случае говорят, что равенства можно сократить на а .

1. Относительно сложения во множестве действительных чисел R любое число регулярно.
2.  Относительно умножения во множестве R регулярным является всякое число, кроме нуля, так, например, 0х2 = Ох 7 но 2 + 7 .
Относительно умножения во множестве R регулярным является всякое число, кроме нуля, так, например, 0х2 = Ох 7 но 2 + 7 .
Нейтральный элемент. Пусть А — множество с бинарной операцией Т . Нейтральным элементом относительно операции Т называют такой элемент е ? А , что равенство еТс = СТе = с справедливо для любого с ? А 
Легко проверить, что если такой элемент существует, то он единственен. Нейтральный элемент, как видно из определения, регулярен.
Как правило, в аДДитивной терминологии нейтральный элемент называют нулем, а в мультипликативной — еДиницеб.
Например, во множестве целых чисел Z нейтральным элементом относительно сложения является число О , а число 1 служит нейтральньџа элементом относительно умножения.
Во множестве Р (А) всех подмножеств данного множества А пустое множество 0 выполняет роль нейтрального элемента относительно операции объединения.
Симметричные элементы. Пусть бинарная операция Т задана на множестве А , обладает нейтральным элементом е . Говорят, что элемент а! ? А симметричен элементу а ? А 
если ата = ата' е. (1)
В аддитивной терминологии симметричный элемент называется противоположным, а в мультипликативной — обратньии к данному.
1. Если а (- R , то число —а R является симметричным (противоположным) элементом относительно сложения. 
2. Если а ? R и а О , то число а— 1 Е R является симметричным (обратным) элементом относительно умножения.
З. Если е — нейтральный элемент, то его симметричным элементом служит он сам, т.к. еТе = е .
Из равенств (1) очевидным образом следует, что если элемент а' е А является симметричным к элементу а ?- А , то а симметричен к а' , т.е. (ау = а.
Следствие 1. Пусть А — множество с ассоциативной бинарной операцией Т и нейтральным элементом е . ТогДа любой элемент а ? А не может иметь более оДноео симметричного элемента.
Д о к а з а т е л ь с т в о. Пусть а1 и а2 — симметричные к а элементы относительно бинарной операции Т . По опреде-
лению, имеем
ата1 аса     
| (2) |
ата2 - ада    
| (3) |
Тогда, очевидно, аТа1 = аТа2, откуда а1Т(аТа1) = а1Т(аТа2). Отсюда, в силу ассоциативности операции Т, получим
(01Та)Т01 — (а1Та)Та2 . Теперь из (2) следует, что еТа1 
 еТа2 и, значит, ат = 02 .
еТа2 и, значит, ат = 02 .
Дистрибутивность. Пусть на множестве А определены две бинарные операции Т и Ш. Говорят, что операция Т Дистрибутивна относительно операции Ш , если для любых а, Ь, с имеет место aT(b с) (ато (атс).
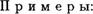
1. На множестве действительных лисел R умножение дистрибутивно относительно сложения:
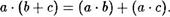
Однако сложение не дистрибутивно относительно умножения.
2. Для операций объединения и пересечения подмножеств произвольного универсального множества справедливы равенства:

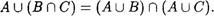
Следовательно, кажДая из этис операций Дистрибутивна относительно Другой.
512. Понятие об алгебраической системе.
Алгебры и модели. Классические примеры алгебр. Изоморфизм алгебр
Пусть А — произвольное множество. В дальнейшем это множество будем называть основным или носителем (построенной) алгебраической системы. Зафиксируем на носителе А некоторые операции F1 , . , Fk и отношения (предикаты)

Пусть тк арность операции Fi(i — К) и тэ— арность отношения Р) (ј 1, s). Положим далее {F1, . 
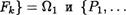 , Рз} = 02.
, Рз} = 02.
Классические алгебры
1. Алгебра с оДнотј бинарной операцией называется группоидом.
Например, каждое из множеств N, Z, Q,R образует группоив относительно операции сложения либо умножения.
2. Алгебра с оДной бинарной ассоциативной операцией называется полугруппой.
Очевидно, все группоиды, указанные в предыдущем пункте, являются полугруппами. Однако в общем случае это утверждение не верно, т.е. масс группоиДов более ШИРОК, чем класс полугрупп.
Например, целые числа относительно операции вычитаНИЯ образуют неассоциатпивныб группоиД.
Приведем другой пример группоида, который не является полугруппой.
Пусть А = {а, b} — двухэлементное множество. Зададим операцию Т на множестве А следующими равенствами:
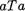 = Ь, аТЬ = а, ЬТа= Ь, ЬТЬ= а.
= Ь, аТЬ = а, ЬТа= Ь, ЬТЬ= а.
Тогда (аТЬ)Та = ата Ь . В то же время аТ(ЬТа) = аТЬ = а, и, значит, (аТЬ)Та аТ(ЬТа) .
Следовательно, операция Т неассоциативна. Это означает, что группоид (А, Т) не является полугруппой.
Заметим, что операции Т , построенной в предыдущем примере, соответствует следующая таблица:

Такие таблицы называются таблицами Кэли. Они используются, как правило, для задания бинарной операции на конечном множестве и устроены следующим образом.
Элементы носителя А записывают в верхней строке и в левом вертикальном столбце. Далее для каждой упорядоченной пары (с, у) „42 результат (СТу) помещается е клетку, стоящую на пересечении строки, соДержащетј элемент с, и столбца, соДержащего элемент у.
В теории полугрупп важнейшую роль играют так называемые полугруппы отображений множеств (в себя)“  Устроены они так:
Устроены они так: 
Пусть А— произвольное фиксированное множество. В качестве носителя полугруппы выбирается множество М (А)  состоящее из всех отображений множества А в себя:
состоящее из всех отображений множества А в себя:
М (А) = {f f : А А — отображение } 
Операцией на множестве М (А) служит КомпоЗицИЯ отображений (гл.П, 5).
Очевидно, что для любых f,g е М(А) их композиция 9 о f также является отображением множества А в себя и, следовательно, g о f М (А) . Ассоциативность операции о компоЗИЦИИ гарантируется теоремой 1 (гл.П, 5).
Таким образом; (М (А), о) — полугруппа для любого множества А .
З. Полугруппа (G, Т) называется группой, если она И.,иеет нейтральный элемент, относительно которого любой элемент а Е- имеет симметричный элемент.
Позже будет показано, что это определение избыточно“ ,
т.е. можно некоторые требования в определении ослабить.
С этой целью сформулируем определение группы в мультиплитсатпивнотј терминологии.
ГруппоиД • ) с операцией умножения называется группой, если выполнены слеДующие условия:
1. ма, Ь, с ? ((ab)c = a(bc)) ассоциативность операции умножения 
(элемент е называют при этом правоб еДиницеб);
З. е G-3b 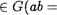 е)
е)
 элемент Ь называется правым обратным для а
элемент Ь называется правым обратным для а 
Условия 1 — З называют аксиомами группы. Опираясь на них, можно доказать, что в группе существует только одна еДинича е , которая является оДновременно и правой, и левот). Нитсагстс Другис еДиниц ни правых, ни левыс не существ ует.
Аналогичное утверждение имеет место и Для элемента, обратного к любому Данному. В связи с этим элемент, обратный к элементу а, имеет стандартное обозначение а—1 
Таким образом, последнее определение группы равносильно исходному, но оно содержит ” меньше“ требований (требуется наличие только правой еДиницы, и для каждого элемента  существование только правого обратного)
существование только правого обратного) 
 Для перевода определения группы на аДДитпивньи) язык достаточно: знак умножения (0 заменить знаком сложения (+) слова ” произведение” , ” единица“ и ” обратный“ , соответственно, — словами ” сумма“ , ” нуль“ и ” противоположныи
Для перевода определения группы на аДДитпивньи) язык достаточно: знак умножения (0 заменить знаком сложения (+) слова ” произведение” , ” единица“ и ” обратный“ , соответственно, — словами ” сумма“ , ” нуль“ и ” противоположныи 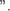
Аксиомы 1 — З будут выглядеть так:
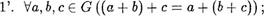
2'. ЗО ? GVa 
3'. G3b е 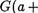
Элемент, противоположный элементу а, обозначается через (—а).
Группа (G, Т) называется коммутативной, либо абелевой, если групповая операция Т коммутатив на, т. е.
Уа, Ь е G(aTb = ьта).
Для абелевыс групп, как правило, используется аДДитивная терминология.
Каждое из множеств Z, Q и R образует группу относи  тельно операции сложения.
тельно операции сложения.
Однако, натуральные числа не образуют ни по сложению, ни по умножению.
Очевидно также, что если в качестве носителя выбрать одно из множеств  Q+, R+ , где Q+, R+ обозначают множества положительных рациональных и действительНЫХ чисел, соответственно, то получим группу относительно умножения.
Q+, R+ , где Q+, R+ обозначают множества положительных рациональных и действительНЫХ чисел, соответственно, то получим группу относительно умножения.
Важнейший класс в теории групп образуют так называемые “группы преобразований“ или ”группы поДстановок 
Преобразованием множества А называется любое биекпивное отображение множества А на себя.
 Зафиксируем множество А, и через S(A) обозначим множество всес биекций f : А А
Зафиксируем множество А, и через S(A) обозначим множество всес биекций f : А А 
S(A) = {fl f : А А — биекция }.
Тогда нетрудно показать, что композиция любых двух отображений из S(A) снова является биекцией (см., напр., упр. 12, с. 47) и, следовательно, .q о f ? S(A) . Таким образом, композиция является бинарной операцией на множестве S(A) . Теперь уже легко установить, что алгебра о) является группой.
Действительно, ассоциативность операции вытекает из теоремы 1 (гл.П, 5). В этой же теореме содержится утверждение о том, что тождественное отображение 1 А множества А играет роль еДиницы при композиции отображений. Следовательно, композиция удовлетворяет аксиомам 1 и 2.
Проверим выполнимость третьей аксиомы. Пусть f Е? S(A) , тогда f : А А— биекция.
Тогда по признаку обратимости отображения существует отображение f—1 : А А, обратное к f, т.е. f o f 1 
—1 -1

 о f 1 А. Это означает, что f — обратимо. Отсюда снова по той же теореме 2 получим, что f—1 — биекция и, следовательно, ? S(A)
о f 1 А. Это означает, что f — обратимо. Отсюда снова по той же теореме 2 получим, что f—1 — биекция и, следовательно, ? S(A) 
Таким образом, и третья аксиома выполняется и, значит,
 о) — группа.
о) — группа.
Если А— конечное множество, то вместо термина ” преобразование“ используется его синоним “поДстановка 
В этом случае, если множество А содержит п элементов, то вместо S(A) используется запись Sn 
Группа Sn называется группой поДстановок п -й степени или симметрической группой п -6 степени. Нетрудно проверить, что она содержит п! элементов.
Пусть (G, Т) и (L, — группоиды.
Определение. ГруппоиД (G, Т) назыв ается изоморфным группоиДу /\L, , если существует боекциЯ р : G L такая, что
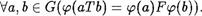
Биекцию р 6 этом случае назыв ают отображением, осуществляющим изоморфизм Данных группоиДов.
Заметим, что условие (*) в словесной формулировке часто выражают словами: “отображение р сосраняет групповую операцию Т 
Из определения очевидным образом следует, что отношеНИе изоморфизма межау группами облаДает свобствами рефлексивности, симметричности и транзитивности.
Запись G .L означает, что группоид Т) изоморфен группоиду (L, Р) .
Нетрудно проверить, что в этом случае, если Т) является группой, то и /\L, Р) — также группа.
П р и м е р ы:
1. Пусть G Z и Т— сложение. Ранее уже отмечалось, что 4) — группа.
Пусть L = {z | z ? Z,z — 2k К ? Z и 17 — умножение (на множестве L ).
Легко проверить, что Е) — группа.
Пусть f : Z L— отображение, определяемое по правилу:
ЛК) 2k для любого К ? Z 
Покажем, что f осуществляет изоморфизм Z .
Действительно, если К2 , то одно из этих чисел меньше другого. Пусть, например, К2 . Тогда, поскольку f— возрастающая функция, то f(k1) < f(k2) , т.е.
 f(k2).
f(k2).
Следовательно, инъективно. Сюръективность отображения f очевидна, и, значит, f — биекция.
Проверим теперь, что отображение f удовлетворяет услоВИЮ ( * 
Пусть К1, К2 ? Z. Тогда f(k1 + К2) — 2k1 +k2 2k1 • 2k2  = f(k1) • f(k2) . Утверждение доказано.
= f(k1) • f(k2) . Утверждение доказано.
2. R+ — множество положительных действительных чисел. Тогда, как уже отмечалось, ( R+ , является группой относительно операции умножения.
Нетрудно проверить, что отображение р : R R , опреДеленное по правилу р(а) lna для любого а ? R+ , осуществляет изоморфизм межау группой (R + , и аДДитпивно1ј группой -Е, •
Действительно, биективность р очевиДна, а условие 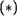 выполняется в силу равенства ln(ab) — ln а + ln Ь для любых а, Ь е R+ (т.е. p(ab) р(а) + p(b) ).
выполняется в силу равенства ln(ab) — ln а + ln Ь для любых а, Ь е R+ (т.е. p(ab) р(а) + p(b) ).
Понятие изоморфизма играет фунДаментальную роль в математике. Из определения следует непосредственно, что изоморфные группоиДы имеют одинаковое количество элементов. Читатель без особого труда докажет, что “еДиница группы при изоморфизме пересоДит (отображается) в еДиницу Другоб группы, элемент, обратный тс Данному, — в обратный  его образу“ и т.д. Несколько больших усилий требуется для понимания и доказательства следующего (более общего) утверждения: ”Если некоторая формула ИСЧИСЛеНИЯ преДикатов истинна на оДной из изоморфныс межДу собой группас, то она истинна и на Другой ”.
его образу“ и т.д. Несколько больших усилий требуется для понимания и доказательства следующего (более общего) утверждения: ”Если некоторая формула ИСЧИСЛеНИЯ преДикатов истинна на оДной из изоморфныс межДу собой группас, то она истинна и на Другой ”.
Другими словами, изоморфные группы имеют оДинаковые алгебраические свойства (т.е. свойства, сформулированные в общелогических терминах и терминах операций, с помощью которых заданы данные группы) 
Это замечание справедливо и для любых алгебр, изоморфных между собой. Однако понятие изоморфизма для произвольных алгебр нами еще не дано. Приведем его.
Заметим, что если результат бинарной операции Т над элементами а1 и а2 записывать через т (щ , (12), то условие  примет вид:
примет вид: 
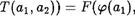 р(а2)).
р(а2)).
В этом виде оно легко обобщается на любую п -арную операцию. А именно, пусть (G, Т) и ф, — оанотипные алгебры с одной п -арной операцией Т, F, соответственно. Тогда биекпивное отображение р : G L называется изоморфизмом, если выполняется условие

В этом случае также говорят, что отображение р сосраняет операцию Т.
Определение. Пусть (G, Т! , тк) и F1, . . .Fk>— одНОТИПНЫе алгебры. Тогда биекциЯ р : 6' L называется изоморфизмом, если она сосраняет кажДую из операций
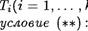 К) , т.е. для каждого i ? {1, К} выполняется
К) , т.е. для каждого i ? {1, К} выполняется
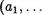 ,ant)) =
,ant)) = 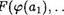 . , р(ап;))
. , р(ап;))
для любых (11, . ати ( есть арность операции 1'i ) 
Пусть Т) — некоторая группа и S — непустое подмножество в G , замкнутое относительно операции Т , т.е.
Уа, Ь ? S(aTb ? S).
Тогда очевидно, что (S, Т) является группоиДом. Группо  ид (S, Т) называется поДгруппоб группы Т) , если он сам является группой, т.е. на множестве S выполняются аксиомы 1 — З.
ид (S, Т) называется поДгруппоб группы Т) , если он сам является группой, т.е. на множестве S выполняются аксиомы 1 — З.
Следующая теорема указывает на особую роль групп подстановок в общей теории групп.
Теорема Кэли. Любая конечная группа изоморфна некоторой поДгруппе группы Sn поДстановок (действующих на носителе этой группы 
Таким образом, при исследовании свойств конечных групп достаточно ограничиться классом всех подгрупп групп подстановок.
Заметим, что современная теория групп своим зарождением и дальнейшим развитием обязана группам- подстановок.
Понятие группы было введено в 1830г. французским математиком Эваристом Галуа, который успешно использовал понятие группы подстановок для решения знаменитой проблемы об условияс разрешимости алгебраическис уравнений в радитсалас.
4. Алгебра (К, -е, •У с Двумя бИНЧНЫМИ операциями — сложением U умножением — называется кольцом, если выполнены следующие условия (аксиомы кольца):
1) Относительно сложения элементы множества К образуют абелеву группу, т. е. алгебра (К, -Е, — абелева группа.
2) Умножение ассоциативно в К , т.е. алгебра (К, является полугруппой.
З) Умножение Дистрибутивно относительно сложения,
т.е. выполняются слеДующие тожДестеа:
Уа, Ь, с ? К ( (а + = ас + Ьс),
Уа, Ь, с ? + Ь) = сан- cb).
Группа (К, -Е) при этом называется аДДитивной группой, а полугруппа КК, » - мультипликативной полугруппойкольца К 
Заметим, что первая аксиома является конъюнкцией аксиом, входящих в определение абелевой группы.
П р и м ер ы:
Целые числа относительно сложения и умножения образуют кольцо р, -е, » •
Если в этом предложении заменить Z на любое из множеств Q или R , то также получим кольцо.
Читатель, знакомый с арифметикой матриц, без труда поймет, что если основное множество К (носитель) некоторого кольца (К, + , заменить множеством всес кваДратныс матриц фиксированного порядка с элементами из К , то снова получим кольцо.
Легко проверяется, что множество четныс целыс чисел также является кольцом.
Однако натуральные числа кольца не образуют, (N, не является группой.
Если умножение в кольце К коммутативно, т.е. ab = ба для любых элементов а, Ь е К , то кольцо К называется коммутатиеным.
Например, все кольца с числовыми элементами коммутативны. Но кольца, элементами которых служат матрицы, могут не обладать таким свойством. Например, кольцо всес матриц с целыми элементами не является коммутативным.
Если мультипликативная полугруппа кольца К содержит еДиницу, т.е. такой элемент е , что ае — еа = а для любого элемента а ? К , то этот элемент е называется единичей кольца К , а само кольцо К — кольцом с еДиницеб.
Например, кольцо Z целых чисел, а также кольцо всех квадратных матриц фиксированного порядка с элементами из Z имеет единицу. Напротив, кольцо четныс целых чисел является кольцом без еДиницы.
Из определения кольца непосредственно вытекают следующие свойства:
1. Уа, Ь, — = ас — bc].
са — cb]
т. е. умножение дистрибутивно относительно вычитания).
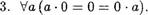
4. Если кольцо К с еДиницей е соДержит более одного элемента, то е О 
Действительно, если допустить, что е 0 , то для любого элемента а ? К получим а а е = а • О = О. т.е. К = {О}  Противоречие с условием.
Противоречие с условием.
Всякое кольцо, содержащее более одного элемента, называется ненулевым.
Пусть К — ненулевое коммутативное кольцо с единицей е . Элемент а ? К называют обратимым, если существует элемент элемента Ь ? К такой, что ab = ба = е. При этом элемент Ь называют обратным к а . Нетрудно установить, что если элемент, обратный тс а, существует, то он еДинственен (см. доказательство следствия из теоремы 2, 5, гл.П).
Поэтому элемент, обратный к а, имеет стандартное обо-
значение а—1 
Приложив небольшие усилия, читатель может доказать, что обратимые элементы кольца образуют группу относителВно умножения. Эта группа называется мультипликативной группой Данного кольца. Например, мультипликативная группа кольца Z целых чисел состоит из чисел 1 и —1.
Ненулевое коммутативное кольцо Р с еДиницей называется полем, если кажДыб его отличный от нуля элемент об-
ратим.
Например, каждое из колец Q и R , рациональныс и Действ ительныс чисел, соответственно, является полем. Напротив, кольцо Z целыс чисел полем не является.
Заметим, что в любом поле Р мультипликативная группа состоит иЗ всес ненулевыс элементов.
У п р аж н е н и я:
1. Пусть р : А В— биекция и С— правильная часть множества А (см. с. 16). Докажите, что р(С) — правильная часть множества В .
2. Какие из отношений, определенных ниже, рефлексивны, симметричны, антисимметричны, являются отношением частичного порядка, либо эквивалентностью?
(а) отношение параллельности (перпендикулярности) на
множестве прямых плоскости;
(Ь) отношение подобия треугольников;
(с) отношение коллинеарности векторов;
(d) отношение R на множестве Z целых чисел, определенное по правилу (а, Ь) е R (а — Ь)/5 е Z;
(е) отношение ” включения“ на множестве всех подмножеств некоторого универсального множества.
З. Будет ли отношение делимости, т.е. отношение, определенное по правилу (а, Ь) ? R а делитель Ь, отношением частичного порядка:
(а) на множестве N натуральных чисел? (Ь) на множестве Z целых чисел?
4. Сколько различных бинарных отношений существует на множестве, состоящем из п элементов?
5. Докажите, что всякое антирефлексивное и транзитивное ОТНОШение (т.е. отношение строгого порядка) является антисимметричным. 6. Докажите предложение, сформулированное на с. 54 
7. Докажите равенства
С -1 ) -1 (F0S) -l = S -1 —1 для любых бинарных отношений F и S.
8. Докажите, что для любых отношений F и S, определенных на данном множестве А, справедливы следующие свойства:
(а) (Fu S) -1 U s -1 ф) (Fn S) -1 Р-1 ns -1
(d) FC S Р -1 С S -1
9. Пусть F,S, F1, S1 — бинарные отношения, определенные на множестве А . Докажите, что
 — F 0S C F1 0Sl.
— F 0S C F1 0Sl.
10. Пусть — произвольное бинарное отношение на множестве А . Докажите, что отношения FnF—1 и FUF —1 симметричны.
11. Пусть {Xi 'i ? I} — разбиение некоторого множества Х. Доказать, что отношение R на множестве Х, определенное по правилу
(с,у)  3i e
3i e  ХО,
ХО,
является эквивалентностью и найти классы этой эквивалентности.
12. Пусть Е — бинарное отношение на множестве А. Докажите, что F является эквивалентностью тогда и только тогда, когда выполняются оДновременно следующие условия:
(а) Д С F , где Д — диагональ множества А ,
ф) F-i = F•
(с) (F0F= F.
13. Докажите, что ядро любого отображения 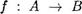
 см. пример 2 с. 60) является эквивалентностью на множестве А.
см. пример 2 с. 60) является эквивалентностью на множестве А.
14. Множество А называется эквивалентным множеству В , если существует биекция р : А В . Этот факт обозначается через А В . Докажите, что отношение  рефлексивно, симметрично и транзитив но.
рефлексивно, симметрично и транзитив но.
15. Докажите, что бинарное отношение, определенное на множестве N х N по правилу
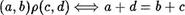
для любых (а, Ь), (с, ф ? N х N, является эквивалентностью.
16. Пусть А— произвольное множество. Тогда А! = AU{c}  где с А называется множеством, полученным из А присоеДпнением одного элемента. Докажите:
где с А называется множеством, полученным из А присоеДпнением одного элемента. Докажите:
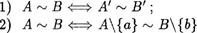 для любых множеств А и В. (Определение отношения см. с. 59.)
для любых множеств А и В. (Определение отношения см. с. 59.)
17. Докажите, что бинарные отношения, определенные на данном множестве, образуют полугруппу с еДиницеб относительно операции композиции.
18. Докажите, что
(а) операция КоМпозИцИи бинарных отношений (определенных на фиксированном множестве) Дистрибу  тивна относительно операции объеДинения;
тивна относительно операции объеДинения;
(Ь) (аПЏ)от 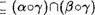 для любых бинарных отношений а, р, Т, определенных на данном множестве.
для любых бинарных отношений а, р, Т, определенных на данном множестве.
19. Докажите, что композиция а о р эквивалентностей а и Д является эквивалентностью тогда и только тогда, когда а о Д = о а .
20. Сколько различных группоидов можно задать на двухэлементном, трехэлементном, и т.д. — на п-элементном множестве.
21. Показать, что если группоид содержит нейтральный элемент, то этот элемент единственен.
22. Укажите, какие из следующих операций на множестве R+ положительных действительных чисел ассоциативны, коммутативны:
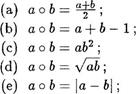
(f) аоЬ— тах{а, b} .
23. Докажите, что множество натуральных чисел относительно каждой из следующих операций является полугруппой:
(а) аоЬ= НОД(а, Ь) 
(Ь) аоЬ= ноща, Ь) 
(с) а о Ь = min{a, Ь} 
(d) аоЬ = а
24. Укажите, какие из следующих множеств образуют полугруппу относительно операции умножения:

25. Пусть Р (А) означает множество всех подмножеств множества А . Какие из следующих операций: (а) пересечение; (Ь) объединение; (с) разность  определяют полугруппу с носителем Р (А) ?
определяют полугруппу с носителем Р (А) ?
26. Докажите, что следующие множества образуют группу относительно умножения (т.е. являются МУЛЬТИПЈШКативными группами):
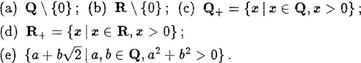
27. Докажите, что следующие множества образуют группу относительно сложения (т. е. являются аддитивными группами) •
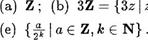 = {3zl z e Z} ; (с) Q ; (d) R
= {3zl z e Z} ; (с) Q ; (d) R 
28. Пусть А {1, 2, 3}. Выпишите все подстановки множества А. Составьте таблицу Кэли, соответствующую операции композиции подстановок.
Известно (см. с. 73), что подстановки на множестве А образуют группу (S(A), о) относительно композиции.
Используя составленную Вами таблицу Кэли, покажите, что группа S3 некоммутативна.
Опираясь на полученный результат, попытайтесь доказать, что группа Sn при п > З некоммутативна.
29. Пусть (К; -6, — кольцо. Докажите следующие свойства:
(Ь) Уа, Ь, се К (аф — с) = ab — ас Л (Ь — с)а = Ьа — со).
Гл ав а Ш
С войс т в а сл о ж е н и я
Из определения операции сложения непосредственно вытекают свойства:
1) Ма N(a+ 1 = Ж).
2) va,b ? N(a+b' 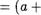
Из доказательства теоремы существования и единственности сложения имеем:
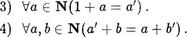
5) Сложение натуральныс чисел коммутативно, т.е.
 (11)
(11)
для любых элементов а, Ь ? N 
Проведем доказательство этого равенства инДукцией по элементу Ь (при фиксированном а 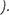
Пусть Ь 1 . Тогда в силу свойств 1 и З получим а + 1 =  а! 1 + а , т.е. равенство (11) при Ь = 1 верно.
а! 1 + а , т.е. равенство (11) при Ь = 1 верно.
Предположим, что оно справедливо при Ь п, т.е. а-{-п 
 п + а— верно.
п + а— верно.
Докажем справедливость равенства (11) при Ь = п! 
Из (1) имеем а + п' (а + п)' , откуда в силу инДуктивного преДположения (т.е. в силу равенства а 4- п = п + б) получим
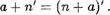
По свойству 2 имеем (п + а)! = п + а! , откуда в силу свойства 4 вытекает, что (п + ау 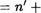
Отсюда, используя равенство а+п' (п+а)' , получим, что а + п! + а. Это означает, что равенство (11) справедливо при Ь п! 
Теперь, учитывая, что число а выбиралось произвольно, приходим к выводу, что равенство (11) справедливо для любых
6) Сложение натуральныс чисел ассоциативно, т.е.
 (12) для любых а, Ь, с ? N .
(12) для любых а, Ь, с ? N .
Д о к а з а т е л ь с т в о. Зафиксируем произвольные числа а, Ь и провеДем инДукцию по с.
Пусть с = 1 . Тогда по свойству 1 имеем (a+b)+1 (a-Fb) f 
С другой стороны, (а + Ь)! — а + Ы по свойству 2. Отсюда
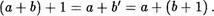
Таким образом, при с — 1 равенство (12) верно.
Предположим теперь, что
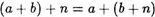
для некоторого числа п N 
Докажем, что равенство (12) верно при с = п! .
Согласно свойству 2 справедливо равенство (а + Ь) + — — ((а + Ь) + п)! , откуда в силу индуктивного предположения получаем
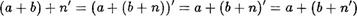
(последние два равенства в этой цепи справедливы в силу свойства 2).
Таким образом, (а + Ь) + п' а + (Ь + . Утверждение доказано.
7) Сложение уДовлетворяет законам сокращения:
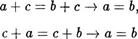 (13)
(13)
для любых чисел а, Ь, с N 
Д о к а з а т е л ь с т в о. Поскольку сложение коммутативно, то достаточно доказать только первую импликацию.
Зафиксируем числа а, Ь . Тогда формула

будет одноместным предикатом от переменной с . Проведем индукцию по с.
Пусть с = 1 и а + 1 = Ь + 1 , т.е. а! — Ы Тогда а = Ь по аксиоме Р4. Таким образом, формула (13) верна при с 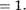
Предположим, что импликация (13) верна при с = п, т.е. из а + п = Ь + п следует а = Ь.
Докажем справедливость импликации

Пусть а + п! = b+n' . Тогда (а + п)! (Ь + п)' в силу свойства 2, откуда по аксиоме Р4 следует а+п = b+n и, далее, по индуктивному предположению получим а = Ь . Утверждение доказано.
Замечание. Алгебра -е) является коммутативной полугруппой, в которой выполняется закон сокращения.
Эта полугруппа называется аДДитивной полугруппой натуральных чисел.
Умножение натуральных чисел
Определение. Умножением натуральных чисел называется бинарная операция П , опреДеленная на множестве N натуральныс чисел и уДовлетворяющая слеДующим условиям аксиомы умножения 
1') а П 1 = а Для любого а Е N;
2') а П Ы = а П Ь + а Для любыс а, Ь N.
Теорема (существования и единственности умножения)  Умножение натуральныс чисел существует и еДинственно.
Умножение натуральныс чисел существует и еДинственно.
Д о к а з а т е л ь с т в о этой теоремы проводится по той же схеме, что и доказательство соответствующей теоремы сложения. При этом, очевидно, нужно заменить всюду символ Т на П и произвести коррективы с учетом условий 1') и 2'). Например, вместо равенства 1131 п = п! записать 1 ГЛ1 п = п , а равенство (5) заменить равенством
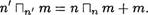 (5')
(5')
Предоставляем читателю провести это доказательство в качестве упражнения.
В дальнейшем для обозначения операции умножения используется стандартный знак • (точка). Результат а ПЬ умножения называется произвеДением чисел а и Ь и обозначается через а • Ь либо — ab 
Конечные множества
Из свойств 1, 2 и 10 следует, что отношение < является строгим поряДком. Модель , т. е. множество N натуральных чисел с отношением ” меньше“ , называют рядом натуральныс чисел.
Отношение < , определенное по правилу ” а Ь тогда и только тогда, когда а < Ь либо а Ь“, очевидно, будет линебным поряДком на множестве N.
Отношение > , двойственное к < , называется ” больше”
т.е. по определению а > Ь Ь а 
Отметим некоторые очевидные свойства ряда натуральных чисел .
1. ЕДиница является Напл№НЬШИМ элементом ряда натуральныс чисел (следует из свойства 4).
2. В ряду натуральных чисел нет наибольшего (вытекает из свойства 3) 
Понятие наименьшего и наибольшего элементов было дано ранее (59, гл.П).
Другие свойства ряда натуральных чисел будут приведены
ниже.
Непустое поДмножество А множества N называется ограниченным сверху, если
За е NVc е < а).
При этом элемент а называется верснеб границей множества А 
Теорема 1 (о наибольшем натуральном числе). Всякое непустое ограниченное сверсу множество натуральныс чисел соДержит наибольшее число.
(Здесь и далее ради краткости фразы ” множество натуральных чисел“ будет использоваться вместо фразы ” подмножество множества N натуральных чисел“ 
Д о к а з а т е л ь с т в о. Пусть О В С N и В— ограничено сверху. Нужно доказать, что во множестве В есть наибольший элемент.
Доказательство будем вести инДукциеб по версней границе множества В .
ПУСТЬ В ограничено сверху числом 1 (т.е. 1 является одной из верхних границ множества В ). Тогда, поскольку В О  то очевидно, что В = {1} и, значит, 1 является наибольшим числом в В
то очевидно, что В = {1} и, значит, 1 является наибольшим числом в В 
Предположим, что утвержДение теоремы справеДливо Для всякого множества, ограниченного сверсу числом п . Пусть В ограничено сверху числом п! , т.е.

Тогда, если п! ? В , то ту — наибольшее в В число. Если же п! В , то Vz б: п/) : откуда в силу свойства 9 отношения ” меньше“ следует Ус < п) . Это означает, что п является верхней границей множества В .
Следовательно, по индуктивному предположению множество В соДержит наибольший элемент. Теорема доказана.
Теорема 2 (о наименьшем натуральном числе). Всякое непустое множество натуральныс чисел соДержит наименьшее натуральное число.
Д о к а з а т е л ь с т в о. Пусть О А С N. Докажем, что во множе стве А есть наименьшее число.
Если 1 ? А , то 1 — наименьшее число в А . Пусть теперь 1 А . Тогда 1 меньше любого числа из множества А . В этом случае образуем множество
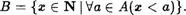
Тогда В О , поскольку 1 ? В 
Кроме того В ограничено сверху любым числом множества А . Следовательно, по предыдущей теореме множество В содержит наибольшее число Ь .
Покажем, что число Ы является наименьшим во множестве А.
Согласно определению множества В получим Уа ? Аф < < а), откуда ввиду свойства 9 отношения меньше“ следует
Уа ? а).
Отсюда легко увидеть, что Ы ? А.
Действительно, если предположить, что Ы А , то высказывание примет вид Уа ? А(Ы < а).
Отсюда по определению множества В вытекает Ы ?- В что в силу Ь < Ы (свойство З отношения меньше“) противоречит выбору числа Ь (оно является наибольшим во множестге В). 
Таким образом, Ы ? А, откуда ввиду ( * ) вытекает, что Ы — наименьшее число в А  Теорема доказана.
Теорема доказана.
 Отрезки ряда натуральных.Определение. Пусть п
Отрезки ряда натуральных.Определение. Пусть п  фиксированное натуральное число. Множество {с 1 < п} называется отрезком ряда натуральныс чисел с м п и обозначается через 1, п]
фиксированное натуральное число. Множество {с 1 < п} называется отрезком ряда натуральныс чисел с м п и обозначается через 1, п] 
Отрезки ряда натуральных облаДаютп следующими се ойств ахи:
1) Для любого натурального числа п имеет место равенство [1 , па = [1, п] U .
Утверждение является очевидным следствием свойства 9 отношения ” меньше“ 
2) 1, п ? [1, п] Для любого натурального числа п . При этом 1 является НашмеНЬШИМ, а п — наибольшим числом во множестве [1, п] 
Свойство очевидно.
З) Для любыс натуральныс чисел п и т выполняется условие
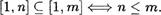
Доказательство предоставляется читателям в качестве упражнения.
4) Для любого натурального числа п отрезок [1, п] является конечным множеством (т.е. не может быть эквивалентен никакой своей правильной части 
Д о к а з а т е л ь с т в о. Применим индукцию по числу п , где п — конец отрезка.
Пусть п = 1. Тогда [1, 1] = 1— одноэлементное множество. Правильной частью его является только пустое множество, которое, очевидно, не может быть эквивалентным одноэлементному множеству.
Предположим теперь, что утверждение справедливо для некоторого фиксированного числа п , т.е. отрезок [1, п] не эквивалентен никакой своей правильной части.
Докажем, что утвержДение справ еДЛИВ0 и Для отрезка [1, па с концом Ж, т.е. что множество [1, па не может быть эквивалентным своей правильной части.
От противного. Пусть
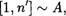 (1)
(1)
где А— правильная часть множества [1, по, т.е. А С Г 1, п'] и А [1, па.
В силу предположения существует биекция р : [1, 
Очевидно, что множество [1, п] является правильной час  тью множества [1, п! Это означает, что множество -41
тью множества [1, п! Это означает, что множество -41  — п]) также является правильной частью множества А (упр. 1, 512 , гл.П).
— п]) также является правильной частью множества А (упр. 1, 512 , гл.П).
Очевидно также, что „41 [1, п] 
Возможны случаи: п' А; п! ? А.
1. Если п' А, то А С [1, п], откуда, поскольку 141  правильная часть множества А, то и „41 является правильной частью множества [1, п]. Это противоречит индуктивному предположению, поскольку „41 [1, п].
правильная часть множества А, то и „41 является правильной частью множества [1, п]. Это противоречит индуктивному предположению, поскольку „41 [1, п].
2. Пусть п! ? А. В этом случае положим „42 А 
Тогда 142 — правильная часть множества А (поскольку п] ? ? А) и п' „42, откуда А = „42 U Тогда условие (1) можно записать в виде
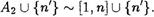
Отсюда, поскольку п! А2 и [1, п], получаем „42 [1, п] (упр. 16, 512, гл.П).
Покажем теперь, что А2 — правильная часть множества
Поскольку т? ? А и А— правильная часть множества [1, пл, то существует элемент т ? [1, по такой, что т А. Отсюда следует, что т п! , поскольку п! ? А и т А. Отсюда ввиду равенства [1, п'] — [1, п] U вытекает, что т ? [1, п]. Поскольку т А, то т „42 и, значит, „42  правильная часть [1, п]. Таким образом, [1, п] „42 и „42 — правильная часть множества 1, п]. Это противоречит индуктивному предположению.
правильная часть [1, п]. Таким образом, [1, п] „42 и „42 — правильная часть множества 1, п]. Это противоречит индуктивному предположению.
Следствие. Всякое множество, эквивалентное некоторому отрезку ряда натуральныс чисел; является конечным.
Д о к а з а т е л ь с т в о. Очевидно, что это утверждение является следствием более общего факта:всякое множество, эквивалентное конечному множеству, само конечно.
Докажем последнее утверждение.
Пусть А — конечно и В А, т.е. существует биекция р : В А . Покажем, что В также конечно.
От противного. Предположим, что В эквивалентно некоторой своей правильной части С , т.е. С С В и С В 
Тогда р(С) А и р(С) А) (упр. 1, 12, гл.п), т.е. р(С) — правильная часть множества А . Отсюда р(С) С
(сужение р на множестве С осуществляет эту эквивалентность).
С другой стороны, С В и В А . Применяя свойство транзитивности отношения эквивалентности между множествами (упр. 14, 12, гл.П), получим АС) А, что невозможно, поскольку р(С) — правильная часть множества А и А— конечно,
В действительности можно доказать утверждение, обратное к предыдущему: всякое непустое конечное множество эквивалентно некоторому отрезку ряда натуральныс чисел.
Опустим это доказательство ввиду его громоздкости. Поэтому последнее утверждение можно также принять за определение конечного множества.
5) Отрезки ряда натуральныс чисел с различными концаМи не эквивалентны.
Д о к а з а т е л ь с т в о. Действительно, пусть п т  Тогда одно из чисел п, т меньше другого.
Тогда одно из чисел п, т меньше другого.
Пусть, например, п т . Тогда в силу свойства З отрезок [1, п] является правильной частью множества [1, т] , откуда в силу предыдущего свойства 4 вытекает требуемое утверждение .
Математической индукции
Теорема 1 (вторая форма метода математической индукции). Пусть Р(с) — некоторый оДноместныб преДикат, опреДеленный на множестве натуральныс чисел. ТогДа если предложение Р(г) справеДливо Для некоторого натурального числа К и Для произвольного натурального числа п К из справеДливости преДложения Р(с) Для всес натуральныс чисел с , уДовлетпворяющис неравенству К < с < п, слеДует справалив ость этого преДложения Для числа п , то это преДложение справеДлиео Для всес чисел с > К 
Д о к а з а т е л ь с т в о. Пусть выполнены все условия теоремы, т.е. для некоторого числа К высказывание Р (К) истинно и для произвольного фиксированного числа п К из формулы Ус(К < с < следует Р (п) . Нужно доказать, что утверждение Р(с) верно для всех с > К .
От противного. Допустим, что существует т > К такое, что Р(т) — ложно. Тогда т > К , поскольку по условию Р(К) —
истинно.
Образуем множество М {с > К Р (с) — ложно }. Тогда М О, так как т М .
В силу теоремы о н а и м е н ь ш е м н а т у р а л ь н о м ч и с л е множество М содержит наименьшее число п .
Отсюда п > К , Р(п) — ложно и ? М (п < с) .
Покажем, что высказывание Vc(k < с < n)P(z) истинно. Заметим, что Р(г) не может быть ложными ни Для какого числа с, уДовлетворяющего неравенству К < аз < п .
Действительно, если предположить, что Р (Ь) ложно для какого-нибудь числа Ь такого, что К < Ь п, то Ь ? М по определению множества М . Но это невозможно в виду того, что Ь п и п— наименьшее число во множестве М.
Таким образом, Ус(К < с < п)Р(с)— истинно, откуда по условию следует, что Р(п) — истинно. Но ранее отмечалось, что Р (п) — ложно. Получено противоречие. Теорема доказана.
Замечание. На практике теорема 1 иногда используется в следующей формулировке: ” Для того, чтобы доказать утверждение Р(с) для всех натуральных чисел с > К, где К — некоторое фиксированное натуральное число, достаточно выполнить два шага:
1-й шаг — установить, что Р (К) истинно;
2-й шаг — для произвольного фиксированного числа п > К проверить справедливость импликации
Vz(k < с <  Р(п')
Р(п')
(для чего, в свою очередь, достаточно предположить, что Р(с) истинно для всех чисел с таких, что К < с < п, и доказать истинность Р (Ы) ) ” 
Последовательность, состоящая из этих двух шагов, называется метоДом математической инДукции во второй форме.
Теорема 2 (третья форма метода математической индукции). Пусть Р (с) — оДноместньиј преДитсат, опреДеленный на множестве ТЧ натуральныс чисел. Тогда, если преДложение Р(с) истинно Для всес чисел некоторого бесконечного подмножества М множества N натуральныс чисел и Для произвольного натурального числа п из истинности Р(п') слеДует истинность Р(п) , то Р(с) истинно Для всес натуральныс чисел.
Д о к а з а т е л ь с т в о. Пусть выполнены все условия теоремы:
1) Существует бесконечное поДмножество М множества N натуральныс чисел, такое что преДложение Р (с) истинно Для всес чисел из М 
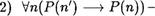 истинно.
истинно.
Нужно доказать, что Р(с) верно Для всес натуральныс чисел.
От противного. Допустим, что утверждение теоремы не верно, т.е. Р(а) — ложно Для некоторого числа а N 
Поскольку отрезок [1, п] является конечным множеством, а множество М бесконечно, то найдется число Ь ? М такое, что [1, п], т.е. Ь.
Образуем множество А = {с с Ь и Р(с) — ложно 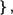 тогда а ? А и, следовательно, А О
тогда а ? А и, следовательно, А О 
По определению множество А ограничено сверху числом Ь , откуда по теореме о н аи б о л ь ш ем н ат у р ал ь н о м ч и с л е множество содержит наибольшее натуральное число с. Тогда с Ь, Р(с) — ложно и Ус А(с < с) 
Докажем, что Р (8) — истинно. Из неравенства с Ь в силу свойства 9 отношения ” меньше“ следует, что 8 < Ь . Действительно, если Ь , то Р(8) — истинно, поскольку Ь ? М  Если с' < Ь , то Р(с') не может быть ложным, так как в этом случае с! ? А , а число с наибольшее в А.
Если с' < Ь , то Р(с') не может быть ложным, так как в этом случае с! ? А , а число с наибольшее в А.
Таким образом, Р (8) — истинно, откуда по условию Р(с) — истинно, что противоречит принадлежности с ? А . Теорема доказана.
У пр аж н е н и я:
1. Докажите теорему существования и единственности умножения натуральных чисел ( 2, гл.Ш).
2. Докажите:
(а) свойство 7 неравенств между натуральными числами ( 5 З, гл.Ш);
(Ь) импликацию (2) в свойстве 8 ( З, гл.Ш);
(с) следствие 2 ( 5 З, гл.Ш);
(d) импликации [1, п] С [1, т] л т п < т;
(е) равенство [1, п']
3. Завершите доказательство теоремы 2 о к о н е ч н ы х м н о ж е с т в ах ( 54, гл.Ш).
4. Докажите теорему З о к о н е ч н ы х м н о ж е с т в ах ( 54, гл.Ш).
Гл ав а IV
ОГЛАВЛЕНИЕ
Предисловие 
 Глава 1. Элементы теории множеств и математической логики
Глава 1. Элементы теории множеств и математической логики
51. Понятие множества
52. Способы задания множеств  .10
.10
53. Операции над множествами  12
12
54. Высказывания и операции над ними  17
17
55. Формулы логики высказываний  . 19
. 19
56. Булевы функции  20
20
57. Понятие об аксиоматической теории  23
23
58. Предикаты  30
30
Глава П. Соответствия, отображения (функции), бинарные отношения и операции  .37 51. Соответствие
.37 51. Соответствие  . 37
. 37
52. Отображение (функция)  38
38
53. Сужение отображения. График. Последовательность  . 39
. 39
54. Типы отображений  41
41
55. Композиция отображений, обратимые отображения  . 43
. 43
56. Бинарные и п-арные отношения  .48
.48
57. Операции над бинарными отношениями  . 51
. 51
58. Свойства бинарных отношений  . .53
. .53
59. Отношение порядка  55
55
510. Отношение эквивалентности  59 511. Операции на множестве
59 511. Операции на множестве  64 512. Понятие об алгебраической системе. Алгебрыи модели.
64 512. Понятие об алгебраической системе. Алгебрыи модели.
Классические примеры алгебр. Изоморфизм алгебр . 68
Глава Ш. Основы аксиоматической теории натуральных чисел  84 51. Аксиомы Пеано и следствия из них.
84 51. Аксиомы Пеано и следствия из них.
Первая форма метода математической индукции 84 52. Сложение и умножение натуральных чисел  . 89
. 89
53. Сравнение натуральных чисел  97
97
54. Ряд натуральных чисел и его свойства. Конечные множества  . 102
. 102
55. Вторая и третья формы метода математической индукции  .109
.109
Глава IV. Целые числа .  .112
.112
51. Кольцо целых чисел  112
112
52. Упорядоченность кольца целых чисел. Теоремы о наибольшем и наименьшем целом числе  121 53. Различные формы метода математической индукции для целых чисел. Теорема о делении с остатком .125 Литература
121 53. Различные формы метода математической индукции для целых чисел. Теорема о делении с остатком .125 Литература  131
131
ПРЕДИСЛОВИЕ
В основу учебного пособия положен курс лекций, апробированный на математическом факультете Волгоградского государственного педагогического университета.
” Вводный курс математики“ является необходимой составной частью учебного плана подготовки будущих учителей математики.
Основная задача состоит в построении общей терминологической базы, необходимой для постановки всех смежных математических дисциплин в педвузе.
В этом курсе заклаДывается фунДамент общеб математической культуры: вводятся основные понятия и вырабатывается язык, который в дальнейшем используется во всех математических дисциплинах на протяжении всего периода обУчения.
Пособие состоит из четырех глав. В первой главе рассматриваются операции над множествами, элементы исчисления высказываний и предикатов. Глава завершается понятием об аксиоматической теории.
Во второй главе изучаются соответствия, отображения, отношения, вводится понятие алгебраической системы и приводятся примеры основных классических алгебр (группоид, полугруппа, группа, кольцо и поле) 
В третьей главе строится эскиз аксиоматической теории натуральных чисел на базе аксиом Пеано, определяются операции сложения и умножения, вводится отношение порядка, изучаются свойства построенной системы. В ней также рассматривается связь между отрезками ряда натуральных чисел и конечными множествами. Глава завершается обоснованием различных форм метода математической индукции (для натуральных чисел).
Четвертая глава естественным образом продолжает третью. Здесь строится кольцо целых чисел, вводится понятие об упорядоченном кольце и изучаются свойства упорядоченности в кольце целых чисел, обобщаются различные формы метода математической индукции для целых чисел.
При написании данной книги автор хорошо осознавал, и в этом его убедила многолетняя практика, что этот курс нелегок для освоения студентами. Это объясняется в первую очередь наличием большого объема базовых понятий и, во-вторых, необходимостью его строгого изложения.
Поэтому автор стремился иллюстрировать понятия примерами, с этой же целью в книге приведено около ста упражнений для самостоятельного решения.
При построении аксиоматической теории натуральных чисел все доказательства проведены подробно, что в свою очередь может вызвать обратный эффект: некое утомление читателя. В этом случае читатель может опустить излишнюю на его взгляд детализацию.
Однако, по мнению автора, каждый математик и, в особенности, преподаватель математики должен хотя бы один раз в жизни детально познакомиться с доказательством основных утверждений о ” первичных“ объектах и отношениях, которые он постоянно использует в своей деятельности.
Пособие адресовано широкому кругу читателей и, в частности, студентам-заочникам. Его программа максимально приближена к школьному курсу математики. Разделы, которые непосредственно не изучаются в школе, могут составить основу факультативных курсов.
Г л а в а 
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И
МАТЕМАТИЧЕСКОЙ ЛОГИКИ 5 1. Понятие множества
“Множество есть многое, мыслимое как еДиное" 
Г. Кантор Теория множеств как математическая дисциплина была создана немецким математиком Г. Кантором (1845—1918) во второй половине XIX в. В основе этой теории лежит одно из основных понятий математики — понятие множества. Согласно идее Г. Кантора, любое множество, являясь с одной стороны совокупностью некоторых объектов, с другой стороны рассматривается как единое целое.
Множество А есть любое собрание определенных и различимых между собой предметов, объектов нашей интуиции или интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества А .
П р и м е р ы:
 множество точек плоскости;
множество точек плоскости;  множество корней квадратного уравнения;
множество корней квадратного уравнения;  множество N — натуральных чисел;
множество N — натуральных чисел;  множество Z — целых чисел;
множество Z — целых чисел;  множество Q — рациональных чисел;
множество Q — рациональных чисел;  множество R — действительных (вещественных) чисел;
множество R — действительных (вещественных) чисел;  множество С — комплексных чисел;
множество С — комплексных чисел;  множество книг в библиотеке;
множество книг в библиотеке;  множество городов России и т.д.
множество городов России и т.д.
К концу XIX в. теория множеств стала играть роль прочного фундамента, на который опирались другие математические дисциплины, в особенности теория функций и арифметика действительных чисел. Результаты, которые были получены с использованием понятий теории множеств, поражали своей строгостью. В адрес теории множеств было высказано много эпитетов. Крупнейший немецкий математик Д.Гильберт говорил: ” Никто не может изгнать нас из рая, который создал нам Г.Кантор” . Французский математик А.Пуанкаре, поразивший своих современников эрудицией и результатами исключительно во всех областях математики, выступая в 1900 году на Втором международном математическом конгрессе, сказал, что в математике достигнута абсолютная строгость“ . Однако, по иронии судьбы, уже в то время было известно о наличии в теории множеств противоречий. Говорят, что теория содержит противоречие, если в ней одновременно Доказуемы Два утвержДения, тсажДое из которыс является отрицанием фугого. В дальнейшем противоречия были названы параДок•сами. В начале ХХ в. количество парадоксов начало расти. Это обстоятельство побудило многих крупнейших математиков заняться пересмотром основ теории множеств. Оказалось, что причины противоречия скрывались как в логике построения теории множеств, так и в несовеошенстве используемого языка. Понятие множества, приведенное в начале параграфа, не может считаться определением, поскольку оно использует термины, толкование которых имеет большую свободу: ” собрание определенных и различимых между собой объектов...“ и т.д. Сами эти термины не имеют точного определения. Исследования вокруг проблемы построения непротиворечивой теории множеств интенсивно велись в течение всего двадцатого столетия. В результате многие параДоксы были сняты за счет преКОНСТРУКЦИИ“ теории множеств. Возникли различные подходы к построению теории множеств. Обнаружились тесные связи между проблемами ” оснований теории множеств“ , философией и математической логикой. Ревизии подверглись практически все математические дисциплины. Однако появились новые проблемы (парадоксы) Другого уровня сложности. Дальнейшее освещение проблем, связанных с развитием теории множеств, выходит за рамки задач данной книги, поскольку оно требует довольно серьезных математических сведений по данному направлению. Отметим лишь, что, несмотря на ” грустный“ оттенок некоторых результатов, работы по пересмотру основ теории множеств привели к бурному развитию всей математики двадцатого столетия. Теория множеств является ярким примером того, что ив математике, как и в любой другой науке, противоречия служат источником развития. Благодаря потрясениям, которые неоднократно испытывала теория множеств, она в настоящее время является фундаментом построения многих математических дисциплин. Оказалось также, что эта теория в том виде, какой она имела в конце XIX и начале ХХ в., после небольшой корректировки может быть использована в качестве базы построения той части математики, которая преподается в высших учебных заведениях нашей страны и за рубежом. Эту часть теории множеств называют ” наивной теорией множеств“ . Ниже мы изложим основные понятия этой теории. Следуя Кантору, описание понятия множества будем вводить постепенно, с помощью соглашений (или требовании)  которым должно удовлетворять это понятие.
которым должно удовлетворять это понятие.
Говоря о множестве, мы считаем, что относительно всякого объекта верно одно и только одно из двух высказываний: либо объект всоДит в Данное множество в качестве его элемента, либо не всоДитп.
Запись ? А означает: г является элементом множества А, если же с не входит в А, то записывают так: с А. Например, 1 ? N, —2 N,v/) Q.
Требование Кантора, что множество определяется своими элементами, может быть сформулировано следующим образом.
Интуитивный принцип объемности. Два множества равны тогДа и только тогДа, тсогДа они состоят из однис и тес же элементов.
Равенство двух множеств записывают в виде А = В, а неравенство множеств А и В — через А В.
Принцип объемности означает, что для доказательства равенства множеств А и В следует выполнить два шага:
1) доказать, что если г ? А, то с (- В;
2) доказать, что если с ? В, то с ? А.
Само множество по опреДелению не является СВоим элементом, А А.
Если множество А состоит из элементов, принадлежащих некоторому другому множеству F , то оно называется поэмножестоом или частью этого множества. Обозначается: А С С F . Символ С обозначает отношение включения. Например:
N C Z CQ C RC C.
Отношение включения множеств обладает свойствами:
1. А С А (свойство рефлексивности), т.е. само множество является своей частью.
2. Если А С В и В С С, то А С С (свойство транзитивности отношения включения 
Если множество состоит только из одного элемента а, то оно называется оДноэлементным и обозначается через {а}  Например, множество корней уравнения 22 — 4 = 0 состоит из одного элемента — числа 2.
Например, множество корней уравнения 22 — 4 = 0 состоит из одного элемента — числа 2.
2. Способы задания множеств
1. Множество может быть записано перечислением всех его элементов:
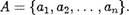
Например, В {0, 1, 2, З, 4},В С 7).
2. Обобщение первого способа состоит в том, что каждый элемент задаваемого множества определяется по некоторому элементу уже известного множества.
Например, считая известным множество целых чисел
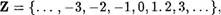
определим множество степеней числа 2: 
2 -3 ,2- , 2 2 , 2 , 2 ,2
З. Задание множества с помощью характеристического свойства Р , выделяющего элементы множества Е  среди элементов более широкого, или основного множества А
среди элементов более широкого, или основного множества А 
Этот способ исходит от Кантора в следующем виде: “КажДое свобстео опреДеляет некоторое множество 
Четкая формулировка его использует понятие ” формы от с или “ формулы от 
Для первоначального ознакомления под формой от с будем понимать некоторое повествовательное предложение Р(с) , содержащее переменное с , которое становится истинным или ложным высказыванием при подстановке вместо с конкретного значения а . Таким образом, форма от с — это некоторое утверждение об с .
Интуитивный принцип абстракции. Любая форма р(с) опреДеляет некоторое множество А , элементами которого являются в точности такие преДметпы а , Для которыс Р(а) — истинное высказыв ание.
Это множество обозначается через Р(с)} и читается: множество всес с , которые облаДают свойством Р .
П р и м е р ы:
R+ = {z с R, с > 0} означает множество положительных действительных чисел;
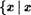 — 52 6 = ()} — множество всех корней уравнения
— 52 6 = ()} — множество всех корней уравнения  - 5х +6 = 0.
- 5х +6 = 0.
4. В дальнейшем мы увидим, что новые множества могут быть заДаны при помощи некоторых операций над иссоДными множествами.
Из принципа абстракции следует существование множества {с т. 74 z} . Это множество, очевидно, не имеет элементов. Из принципа объемности вытекает, что такое множество одно. Оно называется пустым и обозначается символом О 
Пустое множество О является поДмножеством любого множества.
Действительно, если предположить, что включение О С А ложно, то тогда найдется элемент, принадлежащий множеству 0 и не принадлежащий множеству А . Но это невозможно, поскольку О не имеет элементов.
Множеством поДмножеств некоторого фиксированного множества А называется множество, элементами которого являются подмножества множества А . Это множество Р (А) содержит в качестве элементов пустое множество О и само множество А. Например, если А = {а, Ь, с} , то Р (А) 
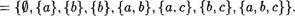
 З. Операции над множествами
З. Операции над множествами
Объединение. Пересечение. ОбъеДинением множеств А и В называется множество А U В, состоящее из всес элементов, кажДый из которыс принаДлежит сотпя бы одному из Данныс множеств,  т.е. А ИВ А или а ? В}.
т.е. А ИВ А или а ? В}.
В частности, если множества А и В заданы с помощью характеристических свойств, например, А 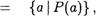
В = {blQ(b)}, то объеДинение состоит из всес тес элементов, которые облаДают хотя бы одним из свойств Р или Q 
ОбъеДинение семейства {Ai i Е I} множеств А; , занумерованных некоторым множеством I индексов, обозначается через
Пересечением множеств А и В называется множество АПВ , состоящее из всес общис элементов Данныс множеств,
 т.е.
т.е.
АпВ
Если таких элементов не существует, то А П В = О. Таким образом, если А = {а Р(а)},В = {b Q(b)}, то пересечение А П В состоит из тес и только тет элементов, которые облаДают оДновременно как свойством Р, так и свойством Q.
Пересечение семейства множеств {Ai i е I} обозначается  через
через
iGI
Заметим, что рисунки, приведенные выше для иллюстрации операций над множествами, принято называть ДиаграммаеИИ Эйлера — Венна.
П р и м е р ы:
1. Пусть А = {2, 5, 7},В = {1, 5,8}. Тогда А U В 

 > = то А ИВ = {c l c ? R , —2 < с}, и АПВ = {г
> = то А ИВ = {c l c ? R , —2 < с}, и АПВ = {г
З. Пусть А — множество всех целых, делящихся на З, а В  множество всех четных целых чисел. Тогда АЛВ — множество всех целых чисел, каждое из которых делится на 6.
множество всех четных целых чисел. Тогда АЛВ — множество всех целых чисел, каждое из которых делится на 6.
Разность. Универсальное множество. Дополнение. Разностью Двус множеств А и В называется множество А В (читается ” А без В л), состоящее из тес и только тес элементов множества А , которые не являются элементами множества В , т.е.
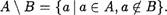
Во многих разделах математики, как правило, изучаются множества, элементы которых принадлежат некоторому фиксированному множеству U 
В этом случае, в целях сокращения математических текстов, множество U называют универсальным и во всех рассуждениях подразумевают, что все рассматриваемые множества являются подмножествами множества U .
Например, в теории натуральных чисел в качестве универсального множества необходимо взять множество N всех натуральных чисел, в планиметрии — множество всех точек плоскости и т.д.
Пусть U — универсальное множество и А С U . Тогда множество А = U А называется Дополнением множества А .
Декартово произведение множеств. Назовем упоряДоченноб парой множество, состоящее из двух элементов, в котором указано, какой элемент считается первым. Обозначается: (с, у). При этом пары (с, у) и (у, с) с с у считаются различными. Две пары (с1, Ш) и (22, У2) считаются равными тогда и только тогда, когда с1 22, У2 .
Аналогично можно определить упорядоченный набор 21, ст • состоящий из п элементов данного множества. Прямым или Декартовым произвеДением Двус множеств Х и У называется множество Х х У , состоящее из всевозможныс упоряДоченныс пар (с, у) , где с Х и у У.
Множество А х А обозначается через „42 и называется Декартовьиа тсваДратом множества А . Декартовой степенью множества А с показателем п N называется множество АП , состоящее из всевозможныс упоряДоченныс п - элементпныс наборов (щ, . , ан) элементов множества А , т.е.
П р и м е р 1. Пусть R — множество всех действительных чисел. Тогда множество R2 R х R состоит из всевозможных упорядоченных пар действительных чисел. Это множество можно интерпретировать как множество точек плоскости, на которой введены декартовы координаты с, у.
П р и м е р 2. Пусть I — отрезок [0, 1] . Тогда 12 - I x I можно интерпретировать как единичный квадрат на плоско  сти (рис. 1)
сти (рис. 1) 
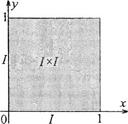
Рис. 1
П р и м е р З. Множество R можно рассматривать как множество точек плоскости, лежащих между параллельными прямыми (рис. 2).

Рис. 2
У п р аж н е н и я:
1. Докажите равносильность следующих условий:
(Ь) Аи В = В
(с) Ап В = А.
2. Докажите, что если множество А состоит из п элементов, то множество Р (А) его подмножеств состоит из  элементов.
элементов.
3. Докажите: для любых множеств А, В, С
(а) если А С В , то А U С С В U С и А п С С В П С ; (Ь) если А С В , то А С С В Х С и С х В С С А .
4. Докажите равенства для любых множеств А, В, С :
ассоциативность операций объединения и пересечения) ;
(Ь) А ив = В U А, А В = В П А (коммутативность);
(d) А П (В U С) = (А 61 В) U (А П С) (дистрибутивность пересечения относительно объединения);
(е) А U (В П С) = (А U В) П (А и С) (дистрибутивность объединения относительно пересечения 
5. Используя свойства операций, сформулированные в упражнениях 1,4, докажите, что, если В С А, то

б. Докажите, что равенство А В = А справедливо тогда и только тогда, когда А П В О.
7. Докажите:

8. Докажите:
(Ь) если В С А, то А С В •
(с) (А) = А (закон инволюции);

(d) (А U В) = А П В и (А В) г: А U В (законы двойственности де Моргана) 
9. Включение А С В будем называть строгим, и множество А — правильной частью множества В , если ЩА 0 (т.е. существует элемент Ь ? В и Ь А).
Докажите, что если А С В и В С С, то множество А является правильной частью множества В тогда и только тогда, когда хотя бы одно из данных включений строгое.
В качестве примера докажем тождество
(А В) С (А П С) (В П С) (упражнение 7, пункт (а) ) 
Пусть с ? (А В) ПС. Тогда с ? А и с ? С, откуда, в силу определений разности и пересечения множеств, с ? А  с В и с ? С. Следовательно, с Е Ап С и с ? В П С и, значит, с (А ПС) (В П С) . Таким образом, (А В) С С
с В и с ? С. Следовательно, с Е Ап С и с ? В П С и, значит, с (А ПС) (В П С) . Таким образом, (А В) С С  (АОС) .
(АОС) .
Докажем обратное включение С пусть е . Тогда с ( АТС) и (ЮС) , откуда с А, с ? С и с В . Следовательно, ? А В и с е С . Это означает, что с ? (А В) С
 4. Высказывания и операции над ними
4. Высказывания и операции над ними
Высказыванием называется всякое предложение, относительно которого разумно говорить истинно тми ложно и которое не может быть оДновременно истинным и ложным.
П р и м е р. Высказываниями являются следующие предложения:
1) ” 5+3 равно 8” 
2) ” 14 делится на 3” 
З) ” Земля вращается вокруг Солнца“ 
4) ” 17 — простое число“ 
5) ” Уравнение с 2 +1 = О не имеет действительных корней“ . Высказывания 1,3,4,5 — истинны, а высказывание 2 — ложно. Логические операции. С помощью логических операций происходит построение нового, более сложного высказывания из некоторых исходных.
1. Отрицанием высказывания А называется высказывание —1,4 , которое истинно тогДа и только тогДа, когДа А ложно.
2.Дизъюнкцией высказываний А, В называется высказывание, которое истинно тогДа и только тогда, когДа истинно сотя бы одно из Данныс высказываний А либо В 
Дизъюнкция высказываний А, В обозначается через А Ч В и читается: А или В 
З.Конъюнкцией высказываний А, В называется высказывание А ЛВ (читается: ” А и В которое истинно тогДа и только тогДа, когДа истинны оДновременно оба высказывания А, В 
4. Импликацией от высказывания А к высказыванию В называется высказывание, которое ложно тогДа и только тогда, когДа А истинно, а В ложно. Это высказывание обоЗначается через А В и читается: ”если А , то В ” или ” А влечет В 
5. Эквиваленциеб двух высказываний А, В называется кОНЪЮНКЦИЯ (А В) л (В А) высказываний (А В) и (В А). Эквиваленция высказываний А, В обозначается
Таблицы истинности. Изучение свойств только что определенных операций во многих случаях удобно проводить с помощью таблиц истинности. Они возникают следующим образом: будем говорить, что высказывание А принимает значение истинности И, если оно истинно, и, соответственно, Л,
если оно ложно.
Таким образом, кажДому из высказываний будет приписан один из символов: И либо Л. При этом значение истинности сложного высказывания будет функцией от значений истинности составляющис его высказываний.
Эта функция определяется некоторой таблицей, которая позволяет вычислять значение истинности сложного высказывания в зависимости от значений истинности высказываний, из которых оно построено, с помощью логических операций.
Например, операция отрицания может быть определена с помощью следующей таблицы истинности.
| и | л | ||
| л | и | ||
Ниже приводится сводная таблица истинности других логических операций: Дизъюнкции, конъюнкции, импликации и эквиваленции.
| А | в | АМВ | Ал В | ||||
| л | л | л | л | и | и | ||
| л | и | и | л | и | л | ||
| и | л | и | л | л | л | ||
| и | и | и | и | и | и | ||
Заметим , что логические операции отражают не связи межДу соДержанием высказываний, а зависимость значения истинности сложного высказывания от значений истинности составляющис его высказываний.
 5. Формулы логики высказываний
5. Формулы логики высказываний
Аналогично тому, как в алгебре с помощью арифметических операций строят сколь угодно сложные выражения из сиМВОЛОВ, обозначающих переменные величины, так и в логике определенные выше логические операции применяются Для построения из Данныс высказываний новыс, более сложныт. Ниже мы дадим определение формулы ЛоГИкИ высказываний. Буквы А, В, С . . . либо А; , Bi,Ci (i ? N) будут использованы для обозначения исходных или элементарных высказываний. Эти символы называются высказывательными переменными.
Понятие формулы логИКИ высказываний определяется следующими соглашениями:
1. Всякая высказывательная переменная есть формула.
2. Символы И и Л — формулы.
3. Если Ф — формула, то — формула.
4. Если Ф и — формулы, то (Ф Ч) , (Ф —» № ) , (Ф Л Ч)  (ф № ) — формулы.
(ф № ) — формулы.
5. Никаких других формул, кроме полученных в соотвеТствии с правилами 1 — 4, не существует.
Замечание. Это определение перечисляет правила построения новыс формул из любого множества исходных формул. Определения такого типа называются инДумпивными.
Так же, как в арифметике. скобки ( , ) служат Для указания послеДовательности Действий при построении формулы.
Для упрощения записи формул примем следующие соглашения об опускании скобок:
1. Будем говорить, что каждый из знаков в ряду Л, М,  4+ сильнее“ любого из знаков, следующих за ним в указанном порядке, т.е. отрицание сильнее“ конъюнкции Л , которая, в свою очередь, ” сильнее“ дизъюнкции и т.д.
4+ сильнее“ любого из знаков, следующих за ним в указанном порядке, т.е. отрицание сильнее“ конъюнкции Л , которая, в свою очередь, ” сильнее“ дизъюнкции и т.д.
2. Будем считать возможным опускать внешние скобки, например, вместо записи (Ф № ) писать Ф 
З. Остальные скобки опускаются таким образом, чтобы при их восстановлении из двух операций более ” сильная“ выполнялась раньше. В этом случае формула может быть названа по последней“ операции. Например, вместо записи  МУ) q) получим импликацию -лФ V q.
МУ) q) получим импликацию -лФ V q.
Булевы функции
Как уже отмечалось, строение формулы позволяет опреДелить ее значение истинности в зависимости от набора значений истинности элементарныс формул, из которых они построены (образованы). Это означает, что кажДая формула опреДеляет некоторую функцию, которая сама и ее аргументы принимают одно из значений И или Л.
Такие функции называются булевыми или функциями ал-
гебры ЛOГИћП.И.
Например, формулу А Л —тВ 'А можно рассматривать как выражение для функции Ф от переменных А, В , значения которой определяются следующими равенствами: Ф (Л,Л) 
 И, = И, = л и
И, = И, = л и 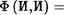 И.
И.
Формула Ф(А, В, . . . , С) логики высказываний называется тожДественно истинной или тавтологией, если она ПРИНИмает значение И при любом наборе значений истинности элементарных формул А, В, . . . , С , из которых она построена.
Например, тавтологиями являются следующие формулы

Формула Ф(А, В, . . . , С) называется тожДественно ложной, если она принимает значение Л при любом наборе значений истинности, составляющих ее элементарных формул А,В,. .. ,С.
Например, формула А Л ЗА тождественно ложна.
Равносильные формулы. Две формулы Ф(А, В, . . . , С) и Ч(А, В, . . . , С) называются равносильными, сли ОНИ опреДеляют одну и ту же булеву функцию. Запись Ф № означает равносильность формул.
Таким образом, Две формулы равносильны в том и только в том случае, если они принимают оДинаковые значения истинности при любом наборе значений истинности составляющис ис элементарныс формул.
Поэтому в равносильности двух формул можно убедиться сопоставлением их таблиц истинности.
Например, из таблицы истинности очевидным образом усматривается равносильность формул АЛ—В  А и А В.
А и А В.

Из определения непосредственно вытекает утверждение:  Две формулы Ф и № равносильны тогда и только тогда, когда их эквиваленция Ф является тавтологией. Другими словами, Ф тогДа и только тогДа, тсогДа Ф Е И“ .
Две формулы Ф и № равносильны тогда и только тогда, когда их эквиваленция Ф является тавтологией. Другими словами, Ф тогДа и только тогДа, тсогДа Ф Е И“ .
Равносильности формул играют важную роль в логических рассуждениях. Поэтому их часто называют законами логики. Приведем основные из них:
1. А —тА Е И (закон исключенного третьего).
П. А Л —1,4 Е- Л (закон противоречия)  Ш. —т—тА Е А (закон двойного отрицания)
Ш. —т—тА Е А (закон двойного отрицания)  IV. А Е А (закон тождества).
IV. А Е А (закон тождества).
V. А ч../ В В V А, А Л В В Л А (законы коммутативности). Ш. А А Е А, А л А Е- А (законы идемпотентности).
VII. (В С) Е- (А V В) мс, Ал (В л С) Е (А Л В) Л С законы ассоциативности 
VIII. АЛ (В V С) Е (Ал В) ч./ (А Л С) (закон дистрибутивности конъюнкции относительно дизъюнкции). IX. А V (В Л С) (А В) Л (А V С) (закон дистрибутивности дизъюнкции относительно конъюнкции).
Х. А Л (А В) —+ В -Е И ( закон отделения 
 (А
(А  В) Л (В С) (А С) И (закон СИЛЛОГИЗМа).
В) Л (В С) (А С) И (закон СИЛЛОГИЗМа).
ХИ. А  В Е —1,4 V В (закон исключения импликации).
В Е —1,4 V В (закон исключения импликации). 
XIII. А  В
В  -м4 В (закон исключения дизъюнкции). ХУ.
-м4 В (закон исключения дизъюнкции). ХУ.  —АЛ—В,
—АЛ—В, 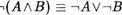 (законы де Моргана
(законы де Моргана 
ХУ. А  В
В  --;В —1,4 (закон контрапозиции).
--;В —1,4 (закон контрапозиции).
Убедиться в справедливости каждой из перечисленных вы-
Ше равносильностей можно, например, с помощью сопоставления таблиц истинности для формул, стоящих в левой и правой частях каждой из них.
Этого можно добиться, не прибегая к таблицам истинности. В качестве примера докажем равносильность формул
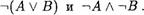
Допустим, что формула —т(А 'V В) принимает значение И, тогда формула А В принимает значение Л. Это означает, что каждая из формул А и В принимает значение Л, откуда следует, что формулы —тА и —тВ одновременно принимают значение И, т.е. —тА Л -лВ принимает значение И.
Пусть  принимает значение Л. Тогда А мВ имеет значение И. Это означает, что хотя бы одна из формул А или В принимает значение И, откуда в свою очередь следует, что хотя бы одна из формул —и4 , —тВ имеет значение Л и, следовательно, —и4 Л —-лВ принимает значение Л. Таким образом, АА V В) —тА Л -лВ .
принимает значение Л. Тогда А мВ имеет значение И. Это означает, что хотя бы одна из формул А или В принимает значение И, откуда в свою очередь следует, что хотя бы одна из формул —и4 , —тВ имеет значение Л и, следовательно, —и4 Л —-лВ принимает значение Л. Таким образом, АА V В) —тА Л -лВ .
Логическое следствие. Пусть Ф(А1 ,  и Ч(А1, , Ап) — две формулы логики высказываний, построенные из элементарных формул 341, .
и Ч(А1, , Ап) — две формулы логики высказываний, построенные из элементарных формул 341, . 
Будем говорить, что формула № (А  А
А  , , Ап) является ЛОГИЧеСКИ.М слеДствием формулы Ф(А А
, , Ап) является ЛОГИЧеСКИ.М слеДствием формулы Ф(А А  , Ап), что записывается так:
, Ап), что записывается так:
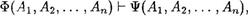
если формула принимает значение И при всес наборас значений истинности элементарных формул „41 , „42, . , Ап , при которых формула Ф истинна. Формула Ф при этом называется посылкой, а № — заключением.
Из определения непосредственно вытекает: Ф Ф тогда и только тогда, когда
ф — тавтология (1)
Например, А А В, А Л В У— А для любых формул
А и В .
Определение логического следствия можно распространить на любое количество посылок следующим образом:
“ Формула № называется логическим слеДствием формул 91, • • . , рп, если № принимает значение И во всес случаяс, когда формулы 91, . . . , истинны. Запись 91, . . , рп н ч будет обозначать, что формула является логическим следствием формул 91, . 
Непосредственным образом проверяется справедливость следующего утверждения 91, . . . , ро Ё— тогДа и только тогДа, тсогДа
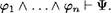 (2)
(2)
Дата: 2019-02-02, просмотров: 515.