Контроль значений признаков и восстановление ошибочных данных

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Для контроля данных найдем:

1. Минимальные и максимальные значения каждого признака в выборке.

2. Оценки математического ожидания значений признаков.

3. Оценим среднего квадратическое отклонение.

4. Стандартные ошибка среднего.

5. Отношение стандартной ошибки среднего к среднему значению.

Минимальные и максимальные значения элементов выборки представлены в таблице 2.1.6.

Таблица 2.1.6. Минимальные и максимальные значения элементов выборки.

	X1	X2	Х3	Х4	Х5	Х6	Х7	Х8	X9
Минимум	10	0	0	0	0	0	11	0	0
Максимум	255	4321	0.0281	243	4386	0.0578	255	4406	0.0246

Для того, чтобы оценить достоверность минимальных и максимальных значений признаков, проведём анализ их основных статистических характеристик.

Среднее – среднее арифметическое значение (оценка математического ожидания):

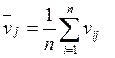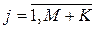, , (2)

где n – количество экспериментальных значений;

M – количество целевых показателей;

К – количество признаков;

v_ij – i–ое значение j–ого признака;

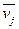– среднее арифметическое значение j–ого признака по n экспериментальным значениям;

i – номер строки (значения признака) в таблицах исходных данных;

j – номер столбца (признака) в таблицах исходных данных.

Далее во всех формулах данного раздела используются одни и те же обозначения переменных, как и в (2), поэтому нет необходимости их дальнейшего пояснения.

Стандартное отклонение (оценка среднего квадратического отклонения) – это мера того, насколько широко распределены экспериментальные данные относительно их среднего значения:

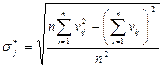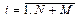; . (3)

Стандартная ошибка среднего – отношение стандартного отклонения к корню квадратному из количества экспериментальных значений:

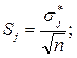
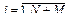. (4)

Отношение стандартной ошибки среднего к среднему значению:

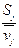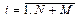; . (5)

Пример расчёта основных статистических характеристик по формулам (2) - (5) для первого признака:

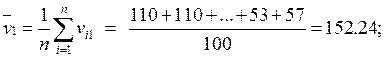
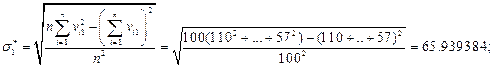
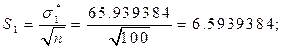
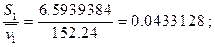
Основные статистические характеристики для всех признаков приведены в таблице 2.1.7.

Таблица 2.1.7. Основные статистические характеристики.

	X1	X2	X3	X4	X5	X6	X7	X8	X9
Среднее значение	152,24	582,29	0,16	99,44	466,91	0,21	152,86	4968,48	0,53
Стандартное отклонение	65,94	1051,49	0,15	64,89	830,94	0,19	68,89	3556,95	0,35
Стандартная ошибка среднего	6,59	105,15	0,02	6,49	83,09	0,02	6,89	355,70	0,03
Отношение стандартной ошибки к среднему	0,04	0,18	0,09	0,07	0,18	0,09	0,05	0,07	0,07

Для решения вопроса о «выскакивающих» (ошибочных) значениях необходимо найти диапазон значений фактора [ a_j , b_j ] ( j =1, M + K ), в котором должно находиться 95% значений фактора выборки:

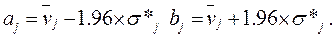
Далее необходимо найти процент значений рассматриваемого фактора непопадающих в этот диапазон. Если таких значений меньше 5%, то считается, что «выскакивающих» значений нет. В противном случае необходимо удалить одно из «выскакивающих» значений (значение наиболее удаленное от оценки среднего) и вновь воспользоваться этой же методикой.

Таблица 2.1.8. Основные статистические характеристики.

	X1	X2	X3	X4	X5	X6	X7	X8	X9
a	23,00	-1478,63	-0,14	-27,75	-1161,73	-0,16	17,84	-2003,14	-0,15
b	281,48	2643,21	0,47	226,63	2095,55	0,57	287,88	11940,10	1,21
% выскакивающих значений	2	5	8	3	6	7	2	0	3

Таблица 2.1.9. Экспериментальные данные. Начало.

№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Y
1	110	5244	0,6583	136	4503	0,4934	210	4867	0,3322	1
2	110	4169	0,587	128	2843	0,4166	136	10802	0,7642	1
3	124	3572	0,482	121	2919	0,4465	201	5664	0,3744	1
4	120	2422	0,4101	127	2132	0,3636	165	6761	0,4983	1
5	69	363	0,2761	178	380	0,1095	116	8303	0,7855	1
6	72	1076	0,4556	176	1086	0,1872	197	5407	0,3733	1
7	137	5681	0,5502	110	4754	0,6268	171	9870	0,581	1
8	17	132	0,6758	237	127	0,0476	86	3086	0,646	1
9	64	1069	0,5109	185	1105	0,1797	158	6009	0,4906	1
10	141	5490	0,0209	102	3624	0,5902	182	7677	0,4814	1
11	119	354	0,1581	133	219	0,1113	94	4357	0,7022	1
12	114	137	0,1027	139	286	0,1217	73	6248	1,0828	1
13	104	182	0,1297	148	346	0,1257	57	7129	1,4813	1
14	102	325	0,1767	150	422	0,137	92	7229	0,9242	1
15	126	142	0,0946	127	379	0,1533	111	1767	0,3787	1

Таблица 2.1.9. Экспериментальные данные. Начало.

№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Y
16	112	512	0,202	139	597	0,1758	114	3356	0,5082	1
17	143	98	0,0692	110	160	0,115	183	5471	0,4042	1
18	106	698	0,2492	145	621	0,1719	64	6473	1,2571	1
19	106	229	0,1428	147	213	0,0993	68	5888	1,1284	1
20	102	1172	0,3356	149	954	0,2073	200	4821	0,3472	1
21	213	314	0,0832	39	266	0,4182	82	8737	1,1399	1
22	201	338	0,0915	51	212	0,2855	84	5258	0,8632	1
23	222	668	0,1164	31	221	0,4796	105	34	0,0555	1
24	220	104	0,0464	33	140	0,3586	166	4555	0,4066	1
25	214	536	0,1082	38	227	0,3965	30	847	0,9701	1
26	234	494	0,095	19	131	0,6024	49	641	0,5167	1
27	230	193	0,0604	23	84	0,3985	240	252	0,0661	1
28	180	275	0,0921	73	189	0,1883	122	6808	0,6763	1
29	231	286	0,0732	22	178	0,6064	29	690	0,9058	1
30	197	589	0,1232	55	666	0,4692	30	306	0,5831	1
31	159	978	0,1967	93	621	0,268	126	5448	0,5858	1
32	159	853	0,1837	92	681	0,2837	217	2553	0,2328	1
33	183	1047	0,1768	70	1014	0,4549	232	378	0,0838	1
34	170	639	0,1487	82	603	0,2995	195	4293	0,336	1
35	202	336	0,0907	50	152	0,2466	95	9068	1,0024	1
36	184	532	0,1254	68	351	0,2755	59	6803	1,398	1
37	170	153	0,0728	83	233	0,1839	147	3878	0,4236	1
38	140	413	0,1452	113	326	0,1598	229	2571	0,2214	1
39	160	525	0,1432	93	454	0,2291	240	47	0,0286	1
40	151	539	0,1538	101	615	0,2455	89	9931	1,1197	1
41	214	696	0,1233	38	464	0,5669	26	345	0,7144	1
42	199	739	0,1366	54	597	0,4525	23	40	0,275	1
43	206	1005	0,1539	47	911	0,6422	15	25	0,3333	1
44	207	541	0,1124	46	462	0,4673	60	2146	0,7721	1
45	224	534	0,1032	29	506	0,7757	74	4001	0,8548	1
46	194	342	0,0953	59	309	0,2979	231	1563	0,1711	1
47	219	525	0,1046	33	321	0,5429	212	4049	0,3001	1
48	220	511	0,1028	32	302	0,5431	167	5135	0,4291	1
49	176	357	0,1074	76	190	0,1814	195	5464	0,3791	1
50	209	989	0,1505	44	730	0,6141	16	143	0,7474	1
51	241	323	0,0746	12	6	0,2041	99	5439	0,7449	0
52	234	292	0,073	19	15	0,2038	253	323	0,071	0
53	237	298	0,0728	16	13	0,2253	231	2554	0,2188	0
54	57	265	0,2856	190	457	0,1125	123	11631	0,8768	0
55	41	158	0,3066	210	286	0,0805	117	11610	0,9209	0
56	67	400	0,2985	180	569	0,1325	161	8027	0,5565	0

Таблица 2.1.9. Экспериментальные данные. Продолжение.

№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Y
57	76	546	0,3075	169	307	0,1037	121	10069	0,8293	0
58	67	112	0,158	185	57	0,0408	123	11732	0,8806	0
59	73	789	0,3848	171	449	0,1239	161	10957	0,6502	0
60	12	20	0,3727	242	41	0,0265	202	6642	0,4035	0
61	139	0	0	115	0	0	255	0	0	0
62	143	22	0,0328	110	183	0,123	248	1098	0,1336	0
63	38	414	0,5354	215	467	0,1005	61	4619	1,1142	0
64	118	113	0,0901	135	14	0,0277	194	5820	0,3932	0
65	173	146	0,0698	78	115	0,1375	136	11727	0,7963	0
66	138	185	0,0986	115	57	0,0657	173	10725	0,5986	0
67	114	111	0,0924	139	23	0,0345	132	10123	0,7622	0
68	139	11	0,0239	114	209	0,1268	201	4320	0,327	0
69	36	398	0,5542	214	348	0,0872	110	11455	0,973	0
70	122	0	0	132	0	0	225	3837	0,2753	0
71	251	418	0,0815	2	0	0	243	628	0,1031	0
72	251	0	0	3	0	0	255	0	0	0
73	251	0	0	3	0	0	255	0	0	0
74	252	0	0	2	0	0	255	0	0	0
75	252	0	0	2	0	0	255	0	0	0
76	165	171	0,0793	88	47	0,0779	186	3969	0,3387	0
77	162	332	0,1125	90	181	0,1495	70	5685	1,0771	0
78	171	176	0,0776	82	59	0,0937	107	9680	0,9195	0
79	176	308	0,0997	77	12	0,045	167	7610	0,5224	0
80	162	258	0,0992	91	16	0,044	132	6186	0,5958	0
81	202	269	0,0812	51	26	0,1	228	3581	0,2625	0
82	203	338	0,0906	50	20	0,0894	246	690	0,1068	0
83	197	118	0,0551	56	78	0,1577	184	5444	0,401	0
84	191	352	0,0982	61	45	0,11	192	5595	0,3896	0
85	182	2	0,0078	71	113	0,1497	161	8901	0,586	0
86	23	56	0,3254	229	415	0,089	127	8757	0,7368	0
87	83	153	0,149	169	339	0,1089	98	8783	0,9563	0
88	89	60	0,087	164	302	0,106	245	287	0,0691	0
89	71	72	0,1195	182	183	0,0743	170	7761	0,5182	0
90	70	70	0,1195	183	167	0,0706	209	5111	0,3421	0
91	234	0	0	20	0	0	255	0	0	0
92	246	410	0,0823	7	0	0	225	3837	0,2753	0
93	247	0	0	7	0	0	255	0	0	0
94	250	0	0	4	0	0	255	0	0	0
95	229	18	0,0185	24	36	0,25	199	6097	0,3924	0
96	46	56	0,1627	206	109	0,0507	120	7824	0,7371	0

Таблица 2.1.9. Экспериментальные данные. Окончание.

№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Y
97	122	83	0,0747	131	196	0,1069	152	7431	0,5671	0
98	85	176	0,1561	166	175	0,0797	148	5123	0,4836	0
99	53	283	0,3174	196	352	0,0957	152	8919	0,6213	0
100	57	329	0,3182	192	378	0,1013	151	9047	0,6299	0

Вывод: После проведения анализа данных выборки, для избавления от выскакивающих значений были удалены строки: 1,2,3,7,8,10,43,45,50,69.

Строки были удалены, поскольку в них содержались значения, не входящие в диапазон (a, b (таблица 2.1.8)):

- 7 строка была удалена из-за показателя X2;

- 1,2,8,69 строки были удалены из-за показателя X3;

- 3,10 строки были удалены из-за показателя X5;

- 43,45,50 строки были удалены из-за показателя X6.

Основные статистические характеристики для признаков сейчас выглядят таким образом, как приведено в таблице 2.1.10.

Таблица 2.1.10. Основные статистические характеристики.

	X1	X2	X3	X4	X5	X6	X7	X8	X9
Среднее значение	143,570	497,220	0,007	107,660	410,090	0,008	145,530	424,440	0,006
Стандартное отклонение	65,045	647,482	0,005	60,705	546,754	0,006	64,085	563,019	0,004
Стандартная ошибка среднего	6,504	64,748	0,001	6,071	54,675	0,001	6,409	56,302	0,000
Отношение стандартной ошибки к среднему	0,044	0,140	0,084	0,058	0,147	0,081	0,043	0,145	0,076

Выборка приведена в таблице 2.1.11

Таблица 2.1.11. Выборка. Начало.

№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Y
1	120	2422	0,4101	127	2132	0,3636	165	6761	0,4983	1
2	69	363	0,2761	178	380	0,1095	116	8303	0,7855	1
3	72	1076	0,4556	176	1086	0,1872	197	5407	0,3733	1
4	64	1069	0,5109	185	1105	0,1797	158	6009	0,4906	1
5	119	354	0,1581	133	219	0,1113	94	4357	0,7022	1
6	114	137	0,1027	139	286	0,1217	73	6248	1,0828	1
7	104	182	0,1297	148	346	0,1257	57	7129	1,4813	1
8	102	325	0,1767	150	422	0,137	92	7229	0,9242	1
9	126	142	0,0946	127	379	0,1533	111	1767	0,3787	1
10	112	512	0,202	139	597	0,1758	114	3356	0,5082	1
11	143	98	0,0692	110	160	0,115	183	5471	0,4042	1
12	106	698	0,2492	145	621	0,1719	64	6473	1,2571	1
13	106	229	0,1428	147	213	0,0993	68	5888	1,1284	1
14	102	1172	0,3356	149	954	0,2073	200	4821	0,3472	1
15	213	314	0,0832	39	266	0,4182	82	8737	1,1399	1
16	201	338	0,0915	51	212	0,2855	84	5258	0,8632	1
17	222	668	0,1164	31	221	0,4796	105	34	0,0555	1
18	220	104	0,0464	33	140	0,3586	166	4555	0,4066	1
19	214	536	0,1082	38	227	0,3965	30	847	0,9701	1
20	234	494	0,095	19	131	0,6024	49	641	0,5167	1
21	230	193	0,0604	23	84	0,3985	240	252	0,0661	1
22	180	275	0,0921	73	189	0,1883	122	6808	0,6763	1
23	231	286	0,0732	22	178	0,6064	29	690	0,9058	1
24	197	589	0,1232	55	666	0,4692	30	306	0,5831	1
25	159	978	0,1967	93	621	0,268	126	5448	0,5858	1
26	159	853	0,1837	92	681	0,2837	217	2553	0,2328	1
27	183	1047	0,1768	70	1014	0,4549	232	378	0,0838	1
28	170	639	0,1487	82	603	0,2995	195	4293	0,336	1
29	202	336	0,0907	50	152	0,2466	95	9068	1,0024	1
30	184	532	0,1254	68	351	0,2755	59	6803	1,398	1
31	170	153	0,0728	83	233	0,1839	147	3878	0,4236	1
32	140	413	0,1452	113	326	0,1598	229	2571	0,2214	1
33	160	525	0,1432	93	454	0,2291	240	47	0,0286	1
34	151	539	0,1538	101	615	0,2455	89	9931	1,1197	1
35	214	696	0,1233	38	464	0,5669	26	345	0,7144	1
36	199	739	0,1366	54	597	0,4525	23	40	0,275	1
37	207	541	0,1124	46	462	0,4673	60	2146	0,7721	1
38	194	342	0,0953	59	309	0,2979	231	1563	0,1711	1
39	219	525	0,1046	33	321	0,5429	212	4049	0,3001	1
40	220	511	0,1028	32	302	0,5431	167	5135	0,4291	1
41	176	357	0,1074	76	190	0,1814	195	5464	0,3791	1
42	241	323	0,0746	12	6	0,2041	99	5439	0,7449	0
43	234	292	0,073	19	15	0,2038	253	323	0,071	0

Таблица 2.1.11. Выборка. Продолжение.

№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Y
44	237	298	0,0728	16	13	0,2253	231	2554	0,2188	0
45	57	265	0,2856	190	457	0,1125	123	11631	0,8768	0
46	41	158	0,3066	210	286	0,0805	117	11610	0,9209	0
47	67	400	0,2985	180	569	0,1325	161	8027	0,5565	0
48	76	546	0,3075	169	307	0,1037	121	10069	0,8293	0
49	67	112	0,158	185	57	0,0408	123	11732	0,8806	0
50	73	789	0,3848	171	449	0,1239	161	10957	0,6502	0
51	12	20	0,3727	242	41	0,0265	202	6642	0,4035	0
52	139	0	0	115	0	0	255	0	0	0
53	143	22	0,0328	110	183	0,123	248	1098	0,1336	0
54	38	414	0,5354	215	467	0,1005	61	4619	1,1142	0
55	118	113	0,0901	135	14	0,0277	194	5820	0,3932	0
56	173	146	0,0698	78	115	0,1375	136	11727	0,7963	0
57	138	185	0,0986	115	57	0,0657	173	10725	0,5986	0
58	114	111	0,0924	139	23	0,0345	132	10123	0,7622	0
59	139	11	0,0239	114	209	0,1268	201	4320	0,327	0
60	122	0	0	132	0	0	225	3837	0,2753	0
61	251	418	0,0815	2	0	0	243	628	0,1031	0
62	251	0	0	3	0	0	255	0	0	0
63	251	0	0	3	0	0	255	0	0	0
64	252	0	0	2	0	0	255	0	0	0
65	252	0	0	2	0	0	255	0	0	0
66	165	171	0,0793	88	47	0,0779	186	3969	0,3387	0
67	162	332	0,1125	90	181	0,1495	70	5685	1,0771	0
68	171	176	0,0776	82	59	0,0937	107	9680	0,9195	0
69	176	308	0,0997	77	12	0,045	167	7610	0,5224	0
70	162	258	0,0992	91	16	0,044	132	6186	0,5958	0
71	202	269	0,0812	51	26	0,1	228	3581	0,2625	0
72	203	338	0,0906	50	20	0,0894	246	690	0,1068	0
73	197	118	0,0551	56	78	0,1577	184	5444	0,401	0
74	191	352	0,0982	61	45	0,11	192	5595	0,3896	0
75	182	2	0,0078	71	113	0,1497	161	8901	0,586	0
76	23	56	0,3254	229	415	0,089	127	8757	0,7368	0
77	83	153	0,149	169	339	0,1089	98	8783	0,9563	0
78	89	60	0,087	164	302	0,106	245	287	0,0691	0
79	71	72	0,1195	182	183	0,0743	170	7761	0,5182	0
80	70	70	0,1195	183	167	0,0706	209	5111	0,3421	0
81	234	0	0	20	0	0	255	0	0	0
82	246	410	0,0823	7	0	0	225	3837	0,2753	0
83	247	0	0	7	0	0	255	0	0	0
84	250	0	0	4	0	0	255	0	0	0
85	229	18	0,0185	24	36	0,25	199	6097	0,3924	0
86	46	56	0,1627	206	109	0,0507	120	7824	0,7371	0
87	122	83	0,0747	131	196	0,1069	152	7431	0,5671	0

Таблица 2.1.11. Выборка. Окончание.

№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Y
88	85	176	0,1561	166	175	0,0797	148	5123	0,4836	0
89	53	283	0,3174	196	352	0,0957	152	8919	0,6213	0
90	57	329	0,3182	192	378	0,1013	151	9047	0,6299	0

Снижение размера выборки.

Исходная выборка разбивается на классы (кластеры), в каждый из которых включаются элементы выборки близкие по значениям факторов и целевого показателя. Необходимость в этом действии возникает в том случае, если выборка имеет большое количество элементов и необходимо снизить объем выборки.

После выполнения кластеризации в выборку включают только типичные представители каждого кластера.

Выводы. В виду того, что количество элементов выборки небольшое (96 элементов) в данном случае снижение размера выборки не производится.

Подготовка файла с выборкой.

При формировании записей файла (выборки) придерживались следующих правил:

1. Элемент выборки - одна строка текстового файла.

2. Разделитель значений факторов – точка с запятой,

3. Числовые данные представлены в формате с фиксированной точкой.

4. Если значение фактора неизвестно, то оно не приводится (указываются подряд две точки с запятой).

5. Значение целевого показателя указывается последним в строке.

6. Первым значением в строке указывается номер элемента выборки.

Подготовка данных для проведения корреляционного анализа

Дата: 2018-12-28, просмотров: 462.

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒