ЛБШ представляет собой описание окрестности пикселя изображения в двоичном представлении. Базовый оператор ЛБШ, применяемый к пикселю изображения, использует восемь пикселей окрестности, принимая значение интенсивности центрального пикселя в качестве порога (рисунок 1.2.4). Пиксели со значением интенсивности большим или равным значению интенсивности центрального пикселя принимают значения равные «1», остальные принимают значения равные «0». Таким образом, результатом применения базового оператора ЛБШ к пикселю изображения является восьмиразрядный бинарный код, который описывает окрестность этого пикселя.
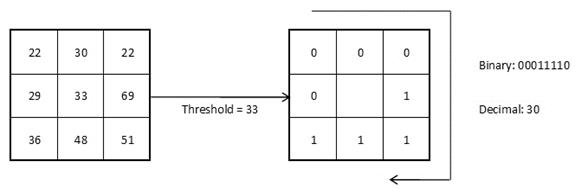
Рис. 1.2.4. Оператор LBR
Обозначения, используемые при построении семантической сети, приведены в таблице 1.2.19.
Таблица 1.2.17. Обозначения. Начало.
| № | Обозначение | Описание |
| 1 | P | Множество точек изображения |
| 2 | p | Точка изображения |
| 3 | X , Y | Множества значений координат точек изображения |
Таблица 1.2.17. Обозначения. Продолжение.
| 4 | x , y | Координаты точек изображения: x: P®X, y :P®Y. |
| 5 | B | Множество яркостей точек изображения |
| 6 | | Яркости точек изображения: : P®B . |
| 7 | l | Величина, которая не превышает расстояния множества точек окрестности точки p изображения |
| 8 | Spl | Яркость точки р |
| 9 | Npl | Множество точек окрестности (расположенных на расстоянии не более l) точки p изображения, Npl = { q / q Î P , r ( p , q ) £ l }где расстояние определяется: ________________________ r (p, q) = Ö ((x(p) – x(q))2 +(y(p) – y(q))2) p Î P , l Îl Î L, L={ l/l , lmax Î 0 £ l £ lmax }. |
| 10 | Bpl | Мультимножество яркостей множества точек окрестности (расположенных на расстоянии не более чем l) точки p изображения: Bpl = < b / b Î B , b = ( q ), q Î Npl >, p Î P , l Îl Î L, L ={ l/ l , lmax Î 0 £ l £ lmax }. |
| 11 | Tpl | Мультимножество параметров множества точек окружности точки p изображения. Значения параметров точек выбираются в зависимости от того больше или меньше значения яркости этих точек в сравнении с пороговым (яркостью точки P). |
Таблица 1.2.17. Обозначения. Окончание.
| 12 | F 0 | Определение множества точек окрестности точки изображения |
| 13 | F 1 | Определение мультимножества яркостей множества точек изображения |
| 14 | F 2 | Определение яркости точки p |
| 15 | F 3 | Изменение значений в точках окружности точки p (0 или 1) |
| 16 | F 4 | Присвоение метки точке p на основе значений в окружающих точках |
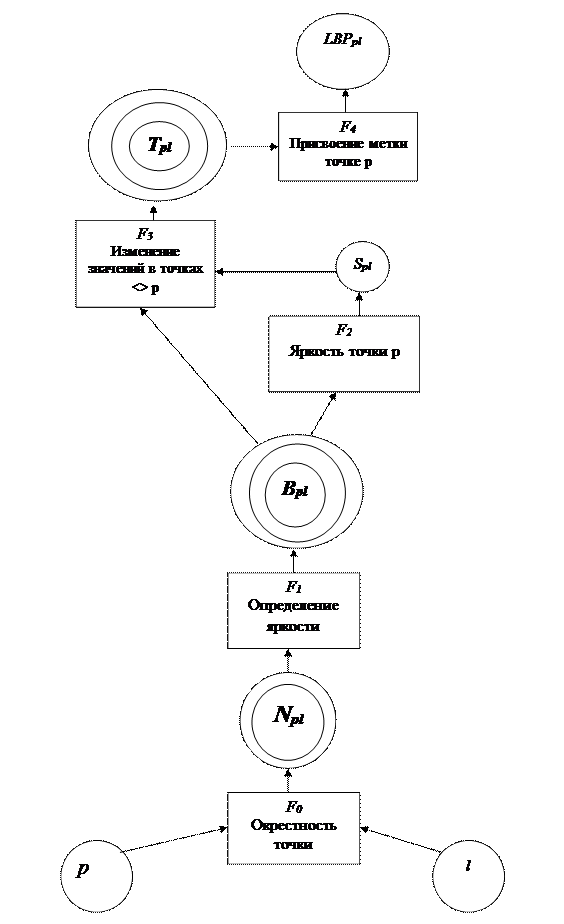Рис. 1.2.5. Выполнение операции LBP
Таблица 1.2.18. Описание функций. Начало.
| Обозначение функции | Описание функции | |
| 1 | N = F 0 ( p, l) | Определение множества точек Nl-окрестности точки изображения p . Пусть задано множество точек изображения P , точка p и расстояние l . Тогда множество N определяется выражением: Npl = { q / q Î P , r ( p , q ) £ l }где расстояние между точками r ( p , q ) определяется: ________________________ r (p, q) = Ö ((x(p) – x(q))2 +(y(p) – y(q))2) p Î P, l Îl Î L, L={ l/ l, lmax Î 0 £ l £ lmax }. Областью определения функции является декартово произведение множеств P и L. Областью значений – множество подмножеств P. |
| 2 | BN = F 1 ( N ) | Определение мультимножества яркостей множества точек изображения. Мультимножество яркостей множества точек изображения определяется с помощью функции: : P®B , где P – множество точек изображения, а B – множество целых неотрицательных чисел, определяющее возможную яркость точек изображения. Пусть задано подмножество N – множества точек изображения P, тогда мультимножество яркостей определяется как: BN = < b / b Î B , b = ( q ), q Î N >. |
Таблица 1.2.18. Описание функций. Окончание.
| 3 | S = F 2 ( B ) | Определение яркости точки p |
| 4 | T = F 3 ( S , B ) | Изменение значений в точках окружности точки p (0 или 1) |
| 5 | LBP = F 4 ( T ) | Присвоение метки точке p на основе значений в окружающих точках |
Коэффициент вариации.
Среднее квадратическое отклонение дает абсолютную оценку меры разброса. Поэтому чтобы понять, насколько разброс велик относительно самих значений (т.е. независимо от их масштаба), требуется относительный показатель. Такой показатель называется коэффициентом вариации и рассчитывается по следующей формуле: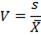 
.
Семантическая сеть на рисунке 1.2.6. Обозначения, используемые при построении семантической сети, приведены в таблице 1.2.18. Пояснения к функциям даны в таблице 1.2.19.
Таблица 1.2.18. Обозначения
| № | Обозначение | Описание |
| 1 | Dpl | Оценка дисперсии яркости окрестности точки |
| 2 | Mpl | Оценка математического ожидания яркости окрестности точки |
| 3 | So | Среднеквадратическое отклонение |
| 4 | Vpl | Коэффициент вариации |
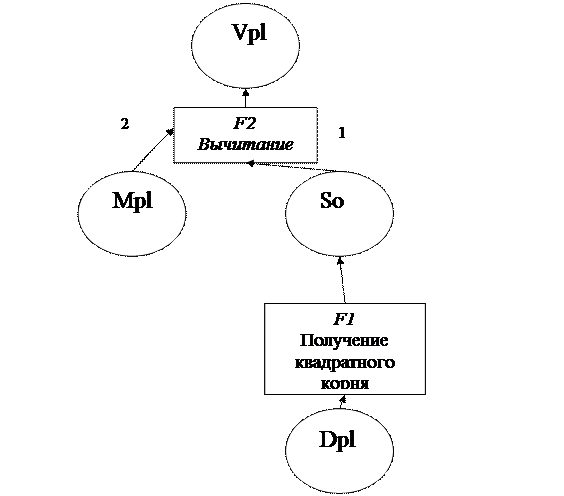
Рис. 1.2.6. Семантическая сеть коэффициента вариации.
Таблица 1.2.19. Описание функций
| Обозначение функции | Описание функции | |
| 1 | So = F 1 ( Dpl) | Математическая операция, результатом выполнения которой является извлечение квадратного корня из аргумента. |
| 2 | Vpl = F2 ( Mpl,So) | Вычитание - одна из вспомогательных бинарных математических операций (арифметических действий) двух аргументов (уменьшаемого и вычитаемого), результатом которой является новое число (разность), получаемое уменьшением значения первого аргумента на значение второго аргумента. |
Дата: 2018-12-28, просмотров: 572.
