1. а) Теперь рассмотрим цепочку из двух реакций первого порядка. Конкретно, пусть в системе в начальный момент времени присутствует только вещество S (в концентрации S0), а с этого момента начинает протекать цепь реакций:
 |
б) Стандартный вопрос: как изменяются со временем концентрации веществ S , P и Z? Будем обозначать эти концентрации теми же буквами (S , P , Z ).
 |
1. Для исходного вещества S дифференциальное уравнение является простейшим:
т.е., несмотря на наличие второй стадии вещество S убывает точно так же, как
если бы этой стадии и не было.
2. а)Для промежуточного вещества Р дифференциальное уравнение таково:
 |
Это линейное дифференциальное уравнение первого порядка.
 |
б) Решение подобных уравнений ищут в виде:
где P0(t) — некая неизвестная функция. Ее-то, очевидно, и следует найти.
 |
в) Подстановка (19.15) в (19.14,б) дает:
 |
откуда
 |
и, после интегрирования,
г) С учетом этого, решение (19.15) принимает вид:
 |
 |
д) Из начального условия (при t = 0 Р = 0) находим константу С:
 |
е) Окончательно получаем:
3. а) Данное выражение описывает колоколообразную кривую (рис. 19.3): концентрация вещества Р вначале растет, а затем начинает падать.
 |
б) Положение максимума определяют, приравнивая нулю первую производную: из условия dP / dt = 0 следует:
 |
в) Заметим, что даваемый этой формулой результат положителен и при k2 > k1, и при k2 < k1. Подставив данное выражение в формулу (19.19), находим саму максимальную концентрацию. После преобразований выражение для нее приводится к виду:
г) Таким образом, Pmax зависит, кроме S0, также от отношения констант скорости, а именно: Pmax тем выше, чем больше отношение константы притока (k1) к константе оттока (k2) (рис. 19.4), где термины «приток» и «отток» относятся к промежуточному продукту.
 |
4. а) Наконец, для конечного продукта цепи (вещества Z) дифференциальное
уравнение таково:
 |
б) Интегрируем с учётом (19.19):
в) Константу С находим из начального условия:
 |
 |
г) Окончательная зависимость:
 |
5. а) Из уравнения (19.22) следует, что производная этой функции — всегда
положительна:
т.е. функция монотонно возрастает.
 |
б) В то же время можно убедиться в наличии точки перегиба, в которой
в) Следовательно, график функции Z(t) – S-образная кривая , как это показано на рис. 19.3. При t → ∞ концентрация конечного продукта стремится к исходной концентрации субстрата (S0).
Дополнительные замечания о последовательных
Реакциях
1 . Случай равенства констант скорости: k1 = k2 ≡ k.
а) При равенстве констант полученные выше формулы, начиная с (19.19), теряют смысл, т.к. превращаются в неопределенности вида 0/0. Для раскрытия неопределенности надо считать одну из констант (например, k2) переменной величиной и применить правило Лопиталя.
б) Так, в случае формулы (19.19) получаем:
 |
 |
в) Убрав ненужный уже индекс, можно записать: при k1= k2
г) Эта функция тоже определяет горбообразную зависимость; так что ничего
принципиально нового в случае равенства констант нет.
д) Для точки максимума получаем следующие выражения (вместо (19.20) и
 |
(19.21)):
Последнее из них учтено на рис. 19.4.
2. Правило лимитирования скорости реакции.
а) Теперь, наоборот, рассмотрим случаи, когда две реакции, образующие цепь, резко различаются по значению констант скорости. Предварительно заметим: скорость процесса в целом, очевидно, определяется скоростью накопления конечного продукта, т.е. величиной dZ / dt = k2P. Выясним, к чему сводится эта скорость в двух крайних случаях.
б) I . Пусть вначале k1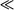 
k2, т.е. первая стадия (рассматриваемая отдельно от второй) является гораздо более медленной. Тогда, с учетом (19.19), получаем:
 |
т.е. константа скорости определяется константой скорости только первой стадии.
II . Если же гораздо более медленной является вторая стадия, то аналогично
получим, что скорость процесса определяется параметрами лишь этой стадии:
 |
в) Обобщая, можно сформулировать следующее правило.
Если стадии цепи реакций значительно различаются по величине констант скорости, то скорость результирующего процесса зависит практиче c ки только от константы медленной стадии.
3. Сопоставление с обратимыми реакциями.
 |
а) Как отмечалось выше, обратимую реакцию тоже можно записать в виде двустадийного процесса:
На этом основании иногда утверждают, что такая реакция — частный случай цепи из двух последователь-
ных «реакций» (случай, когда вещество Z совпадает
с веществом А).
б) Но данная аналогия является чисто внешней. Кинетика же этих процессов принципиально различна. Так, для вещества Р обратимой реакции, как следует из п. 17.2, получим экспоненциальный рост до некоей равновесной концентрации (рис. 19.5), но вовсе не горбообразную кривую, как для промежуточного метаболита цепи.
Дата: 2019-02-02, просмотров: 196.
