Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

а) Первый фактор – специфика реакции – количественно отражается в энергии активации. В качестве последней используют две несколько отличающиеся величины:

- ΔG_ак – энергию Гиббса активации и

 -  Е_ак  –  энергию активации по Аррениусу, или просто энергию активации.

б) В трактовке обеих величин ключевую роль играет представление о том, что молекулы одного и того же вещества существенно различаются по энергии.

в) Поэтому рассмотрим вначале, как образуется такое распределение. Для простоты будем пока иметь в виду лишь кинетическую энергию молекул.

1. Распределение по проекциям скорости на направление. Мгновенную скорость (u)  любой молекулы можно разложить на составляющие по направлениям – u_x, u_y, u_z .

Так вот, прежде всего молекулы различаются по проекциям своей скорости на каждое направление; причём эти проекции постоянно меняются. Тем не менее общий характер распределения проекций остаётся постоянным и характеризуется двумя функциями.

а) F ( u_x ) – интегральная функция распределения, т.е. вероятность того, что проекция скорости – не более значения u_x. Очевидно, с ростом аргумента u_x  указанная вероятность возрастает от 0 до 1 (рис. 18.1,а).

б) Но обычно рассматривают не саму функцию F(u_x), а её производную – плотность вероятности:     

Очевидно, ω(u_x)∙du_x  – вероятность того, что проекция скорости про-извольной молекулы изуча-емой системы лежит в интервале du_x, примыкаю-щем к точке u_x.

I . Распределение проекций и_х является нормальным. Это значит, что оно
описывается следующей формулой:

 

 

II . Центр этого распределения — в нуле (рис. 18.1, б). Действительно, так как частицы с равной вероятностью могут двигаться в обоих направлениях оси х, то
средняя скорость по этой оси равна нулю. Величина 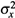— среднеквадратичное
отклонение. Можно доказать, что

где М — молярная масса вещества.

2. Распределение частиц по абсолютной скорости (распределение Максвелла). А как найти распределение частиц по абсолютной скорости и?

а) Величина ω(u_x,u_y,u_z) — это плотность вероятности того, что проекции скорости частицы равны u_x,u_y,u_z (рис. 18.2). Она получается путем перемножения выражений вида (18.2):

 

б) Но некоторое значение скорости и может складываться из большого множества различных комбинаций значений u_x,u_y и   u_z. Величина этого множества определяется (в пространстве скоростей) площадью сферы радиуса и, равной 4πu ². Учитывая это, приходим к распределению частиц по абсолютной скорости:

 

в) Подставим сюда формулы (18.2)—(18.4), учитывая 3 обстоятельства:

В последнем соотношении N — число частиц, а N₀ — общее количество частиц. С помощью этого соотношения переходим от плотности вероятности к числу частиц, имеющих определенную скорость (точнее, к производной числа частиц по скорости).

г) В итоге получаем распределение Максвелла — распределение числа частиц по абсолютной скорости:

 

 

В отличие от нормального распределения, здесь (рис.18.3) максимум распределения и средняя арифметическая скорость находятся не в нуле, а имеют положительные значения, которые, как можно доказать, таковы:

 

 

Ещё больше по величине значение среднеквадратичной скорости:

                                                    

 3. Распределение частиц по кинетической энергии.

а) Наконец, перейдём к распределению частиц по кинетической энергии. Для этого учтём следующее:

б) Отсюда

в) Данное распределение похоже на предыдущее, но является более пологим (рис. 18.4), т.к. и степенная, и экспоненциальная зависимости здесь уже не такие сильные.

г) Исходя из формулы (18.10) или формулы (18.8,в), можно придти к известному выражению (1.2,а) для средней кинетической энергии идеального газа или идеального раствора (в расчёте на 1 моль вещества):

                                                      

В частности, для 298 К получаем: Е_к^ср ≈ 3,7 кДж/моль.