В завершение этой главы уточним, из чего складывается измеряемая ЭДС
элемента.
 |
1. а) Согласно закону Кирхгофа, суммарные падения напряжения (разность по тенциалов) во внешней и во внутренней цепи элемента одинаковы по величине и
противоположны по знаку:
б) Следовательно, речь идет об определении всех слагаемых правой части
этого равенства. Или, как говорят, скачков потенциала во внутренней цепи эле-
мента. Такие скачки создаются на каждой границе фаз в элементе.
2. а) Два из них, причём самые важные, нам уже известны: это рассмотренные в предыдущем пункте электродные разности потенциалов в каждом из двух полуэлементов, ΔΨэ,1 и ΔΨэ,2 (рис.14.7). Они возникают на границах металлических электродов с жидкими фазами полуэлементов.
 |
б) Заметим: записывая для представленного элемента любую разность потенциалов ΔΨ i, следует располагать потенциалы фаз в порядке, противоположном ходу часовой стрелки. С учётом этого,
3. а) Еще две границы раздела — между растворами электролитов. В нашем
случае это границы раствора KCl в солевом мостике с раствором ZnSO4 в одном полуэлементе и с раствором CuSO4 — в другом.
б) Соответственно, говорят о диффузионных разностях потенциалов, ΔΨд,1 и ΔΨд,2, возникающих потому, что ионы (компоненты растворов) отличаются по концентрации (I) и подвижности (II).
I . Так, ионы того или иного вида диффундируют через границу раздела в раствор с меньшей концентрацией именно этих ионов. Например, ионы Zn2+и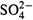 
— в раствор солевого мостика, а ионы K+ и Cl- — в раствор CuSO4.
II . А из-за различия в подвижности эти перемещения происходят с разной скоростью, что и приводит к появлению ΔΨд,i.
в) Рассмотрим сумму величин ΔΨд,1 и ΔΨд,2:
 |
Здесь ΨXY,1 и ΨXY,2 — потенциалы растворa KCl соответственно на границе с первым и вторым полуэлементами.
В силу высокой подвижности ионов К+ и Cl– эти потенциалы можно считать практически одинаковыми (хотя не абсолютно: иначе ионы К+ и Cl– вообще бы не перемещались). Тогда, принимая, что ΨXY,1 ≈ ΨXY,2, имеем:
min (ΔΨд,1 + ΔΨд,2 ) = ΨZnSO4 – ΨCuSO4 . (14.38,б)
г) Таким образом, выбор в качестве солевого мостика насыщенного раствора KCl вовсе не устраняет диффузионную разность потенциалов, а только сводит её к минимально возможному значению, которая определяется природой полуэлементов.
4. Наконец, контактные разности потенциалов, ΔΨK, возникают на границе двух металлов.
а) В случае, изображенном на схеме (рис. 14.7), это границы между проволокой из металла X , соединяющей электроды, и цинковой (ΔΨK,1) или медной (ΔΨK,,2) пластинкой.
б) Поскольку металлы характеризуются разной работой выхода электрона, то при прямом контакте металлов на их границе происходит некоторое перераспределение электронов.
в) Вновь обратим внимание на сумму двух скачков потенциала:
 |
Здесь ΨX,1 и ΨX,2 — потенциалы проволоки в месте соединения с первым и вторым электродами.
 |
г)Если бы во внешней цепи не было сопротивления (представленного, например, вольтметром), а сопротивлением проволоки можно было бы пренебречь, то потенциалы проволоки везде были бы одинаковы — в т.ч. на её концах (выполнялось бы равенство ΨX,1 = ΨX,2), и получалось бы, что
Это означает, что сумма контактных потенциалов не зависит от природы
проволоки X , а определяется только природой электродов.
5. а) В итоге измеряемая вольтметром ЭДС складывается из следующих шести скачков потенциала во внутренней части цепи:
 |
 |
б) Если мы подставим приводившиеся выше выражения для всех этих величин, то при условии (14.39,б) получим просто ноль, т.к. все потенциалы сократятся:
Таким образом, если во внешней цепи нет нагрузки (сопротивления), то элемент не вырабатывает ЭДС.
в) А теперь пусть во внешней цепи содержится сопротивление Rex . В этом случае потенциалы соединительной проволоки в местах контакта с электродами уже не одинаковы, и, как нетрудно убедиться путём такой же подстановки величин в (14.40), измеряемая ЭДС равна разности этих потенциалов:
если Rex ≠ 0 , то ЭДС = ΨX,2 – ΨX,1 . (14.41,б)
г) Причём данная разность максимальна тогда, когда во внешней среде не происходит падения напряжения:
при Rex → ∞ ЭДС → max.
6. Но не означает ли проведённое рассмотрение, что, благодаря влиянию диффузионных и контактных разностей потенциалов, максимальное значение измеряемой ЭДС всё-таки отличается от того значения (ΔΨрц), которое рассчитывается по энергии Гиббса? – Ни в коей мере.
 |
I .. В отсутствие химической реакции для диффузионных потенциалов получаем:
т.к. потенциалы растворов не отличались бы друг от друга. Их различие
создается лишь благодаря тому, что растворы по-разному обмениваются с
металлическими пластинками ионами или электронами.
II . По той же причине равнялась бы нулю и сумма контактных скачков
потенциала (14.39,б), Таким образом, сумма всех скачков потенциала во вну-
тренней цепи элемента имеет своим происхождением только энергию ОВР.
Краткое содержание главы 14
В главе рассмотрены электродные процессы.
1. В ходе одного из них – ЭЛЕКТРОЛИЗА – происходит преобразование электрической энергии в энергию эндергонической ОВР.
2. Другой феномен – ГЕНЕРАЦИЯ ЭДС в гальванических элементах. Здесь, напротив, энергия ОВР преобразуется в электрическую энергию.
Так, в ЭЛЕМЕНТЕ ДАНИЭЛЯ-ЯКОБИ используется энергия следующей реакции:
 |
3. а) При условии, что ток во внешней цепи — БЕСКОНЕЧНО МАЛ, возникающая ЭДС, или ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ реакции (∆Ψрц), однозначно связаны с энергией Гиббса:
 |
б) Отсюда следует зависимость ЭДС от активностей участников (УРАВНЕНИЕ
НЕРНСТА) и от температуры:
4. а) С другой стороны, ∆ψрц можно представить и через ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ:
 |
где Ψ1 — потенциал катода (–), т.е. ОВ-пары, служащей ВОССТАНОВИТЕЛЕМ, а Ψ2 — потенциал анода (+), т.е. пары, служащей ОКИСЛИТЕЛЕМ.
б) Электродные потенциалы принято измерять по водородной шкале (при условии, что у водородного электрода P(H2) = 1атм и рН = 0). Тогда их называют РЕДОКС–ПОТЕНЦИАЛАМИ.
 |
5. Редокс-потенциалы зависят от активностей участников соответствующей ПОЛУРЕАКЦИИ, например:
Эти выражения иногда называют уравнениями Нернста; в других источниках —
уравнениями Петерса.
6. а) СТАНДАРТНЫЕ значения ЭДС (∆Ψ°рц) и редокс-потенциалов (∆Ψ° i) относятся к ЕДИНИЧНЫМ АКТИВНОСТЯМ всех участников. Если среди них – и протоны, то данное условие означает, что рН = 0.
б) Используются также КАЖУЩИЕСЯ значения ЭДС (∆Ψ′рц), относящиеся к условию рН = 7,0.
7. а) В основе механизма генерации ЭДС – обмен ионами или электронами между электродом и раствором.
б) А измеряемая ЭДС складывается, по меньшей мере, из шести СКАЧКОВ ПОТЕНЦИАЛА во внутренней цепи элемента:
ЭДС = – (∆Ψ э, 1 + ∆Ψ э, 2 + ∆Ψ к, 1 + ∆Ψ к, 2 + ∆Ψ Д, 1+ ∆Ψ Д, 2 )
Эти скачки представляют собой разности потенциалов:
ЭЛЕКТРОДНЫЕ (∆Ψэ, i) — на границе металлических электродов с жидкой фазой полуэлементов;
КОНТАКТНЫЕ (∆Ψ к, i) — на границе электродов с соединяющей проволокой, и
ДИФФУЗИОННЫЕ (∆Ψ д, i) – на границе жидких фаз полуэлементов с содержимым cолевого мостика.
Глава 15. ВИДЫ ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ И
ЭЛЕКТРОДОВ. ПОТЕНЦИОМЕТРИЯ
Рассмотрев теоретические аспекты феномена генерации ЭДС в гальванических элементах, перейдем к более практическим вопросам.
В этой главе будут описаны различные виды этих элементов (до сих пор мы имели дело, фактически, только с элементом Даниэля–Якоби), а также соответствующие методы физико-химического анализа.
Дата: 2019-02-02, просмотров: 216.
