1. а) Обратим внимание на знаки: для самопроизвольной реакции (т.е. реакции, идущей в прямом направлении)
 |
Положительный знак ∆ψрц означает, что работа по перемещению единичного положительного заряда от электрода 1 к электроду 2 совершалась бы над системой (п. 1.4); следовательно, перенос отрицательного заряда (каковыми являются электроны) происходит в указанном направлении самой системой.
б) Отсюда вытекает следующая расстановка индексов в записи
 |
1 — восстановитель (донор электронов),
2 — окислитель (акцептор электронов).
в) Соответственно,
Ψ1 — электрический потенциал катода (–): здесь — избыток электронов;
Ψ2 — электрический потенциал анода (+), на котором — дефицит электронов.
 |
2. а) Следовательно, обобщенную ОВР, за счет которой генерируется ЭДС в
гальваническом элементе, следует записать в виде
где фигурируют две окислительно-восстановительные пары (ОВ-пары):
- пара 1 (Ox1/Rd1) — служит в реакции восстановителем и образует катод,
- и пара 2 (Ox2/Rd2) — служит окислителем и образует анод.
б) Заметим: в записи отдельной окислительно-восстановительной пары первой указывается окисленная форма.
3. В результате, например, для элемента Даниэля—Якоби (рис. 14.1 и (14.5))
необходимо полагать:
 |
поскольку в происходящей в этом элементе реакции первая из указанных пар
является восстановителем, а вторая — окислителем.
14.8. Зависимость ∆Ψрц от концентраций участников ОВР
И от температуры
1. Зависимость от концентраций.
а) Вспомним уравнение изотермы реакции:
 |
 |
которое определяет зависимость энергии Гиббса от концентраций (активностей) участников. Здесь ΔG °рц – стандартное значение этой энергии; оно соответствует реакции при постоянных одномолярных концентрациях всех реагентов и продуктов. А Па – произведение активностей, которое для обобщённой ОВР вида (14.14) равно:
б) Подставим (8.35,б) в формулу (14.12,б). Тогда получаем уравнение Нернста:
де
u
Здесь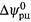 
— стандартная ЭДС реакции {стандартный электрический потенциал реакции). Эта величина, как и ΔG °рц, соответствует ситуации, когда в полуэлементах поддерживаются одномолярные активности всех участников.
в) Вместе с тем, благодаря соотношению (4.35), стандартная ЭДС реакции просто связана с константой равновесия той же реакции (14.17,в).
г) Итак, уравнение Нернста (14.17,а) устанавливает зависимость ЭДС гальванического элемента от концентраций (активностей) участников ОВР.
Конкретно: чем меньше Па, тем больше генерируемая ЭДС. Важно отметить, что при этом учитываются активности веществ в обоих полуэлементах.
2. Зависимость от температуры.
а) А здесь воспользуемся формулой (5.13, а)
 |
которая следует из соотношения
 |
при условии, что энтальпия и энтропия реакции практически не зависят от
температуры. Подстановка (14.17,б) дает:
б) Производная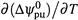 
называется температурным коэффициентом ЭДС. Как видно, этот коэффициент полностью определяется энтропией реакции. Отсюда вытекает, что сама зависимость 
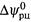от температуры является линейной.
 |
в) С другой стороны, измеряя ЭДС гальванического элемента при разных температурах, производную
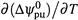можно оценить из экспериментальных данных. Тогда легко найти не только энтропию реакции (исходя из (14.18)), но и энтальпию, т.е. (вместе с энергией Гиббса (14.17,в)) все три термодинамические характеристики соответствующей ОВР. Действительно,
или
 |
г) Итак, чтобы воспользоваться данной формулой, надо знать производную
стандартной ЭДС по температуре, а также конкретное значение стандартной
ЭДС при какой-либо температуре.
Электродные потенциалы
1. а) В практических расчетах часто используют не только ЭДС самой реакции (ОВР), т.е. разность потенциалов между электродами — ∆Ψрц, но и потенциалы отдельных электродов — Ψ1 и Ψ2; они же — потенциалы соответствующих окислительно-восстановительных пар:
 |
б) Из того факта, что величина ∆Ψрц зависит от концентраций участников ОВР, следует аналогичная зависимость и для электродных потенциалов.
Однако каждый такой потенциал, очевидно, зависит от концентраций
участников только своей полуреакции.
 |
2. а) Чтобы найти эту зависимость, надо в уравнении Нернста (14.17,а) разделить величины, относящиеся к разным полуреакциям:
В частности, стандартная ЭДС (∆Ψ0рц) представлена как разность стандартных потенциалов, относящихся к единичным активностям всех компонентов соответствующей окислительно-восстановительной пары.
 |
б) I . Сопоставляя (14.21, б) с (14.20), для потенциала любой пары (любого электрода) можно записать выражение:
 |
II . Если стехиометрические коэффициенты в уравнении полуреакции (α и β)
отличны от 1, то, очевидно, формулу надо несколько усложнить:
III . Наконец, если в уравнении полуреакции, кроме основных компонентов ОВ-пары, фигурируют другие ионы, например, протоны (как часто бывает в случае органических веществ), то их активность, естественно, тоже входит в формулу расчета потенциала. Так, для полуреакции
 |
 |
потенциал равен
3. а) Эти формулы и определяют зависимость электродного потенциала от активностей участников полуреакции.
а) Если все активности равны 1, то потенциал равен стандартному.
б) В противном случае потенциал тем больше, чем сильнее сдвинуто соот-ношение активностей в сторону окисленной формы, т.е. чем выше сродство пары к электронам.
в) И, как следует из (14.23,б), потенциал может зависеть от рН среды.
Полученные нами выражения фактически являются разновидностями
уравнения Нернста, отчего данное название нередко используют и для них,
хотя в некоторых учебниках их называют уравнениями Петерса.
4. Другие формы записи ур-я Нернста (Петерса).
 |
а) Часто обсуждаемые уравнения записывают для Т = 298 К и одновременно переходят от натуральных логарифмов к десятичным. Тогда, например, выражение (14.22, б) приобретает вид:
б) Нередко активности тех или иных участников полуреакции следует принять за 1. Это относится к веществу
- в твердой фазе (например, металлической меди в паре (Сu2+/Cu)),
- или в газообразном состоянии, если давление вещества равно нормальному атмосферному давлению.
в) В общем же случае активность газообразного участника (например, H2)
равна отношению его давления к стандартному:
 |
5. Используем сделанные замечания для электродов элемента Даниэля—
Якоби. Кроме того, учтем, что в этом случае z = 2, так что 0,059/z ≈ 0,03В.
Тогда получаем выражения вида:
 |
 |
которые, по существу, аналогичны формулам для химического потенциала:
Дата: 2019-02-02, просмотров: 232.
