Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

И элементов

Кроме вышеизложенного, существуют и другие принципы подразделения электродов и элементов. Так, и те, и другие могут быть обратимыми и
необратимыми.

1. а)Обратимые электроды таковы, что если с помощью внешней ЭДС изменить направление тока в цепи на противоположное, в полуэлементе пойдет
обратная полуреакция.

б) В элементе Даниэля—Якоби оба электрода — обратимые:

 

в) Обратимые электроды, в свою очередь, могут быть двух видов.

I . Обратимые по катиону: электроды и раствор обмениваются катионами. В
основном, это электроды первого рода: электроды элемента Даниэля–Якоби
(медный и цинковый), водородный электрод и др. Потенциал таких электродов определяется активностью соответствующего катиона в растворе.

II . А в обратимых по аниону электродах происходит обмен (между твердой
фазой и раствором) анионами; соответственно, от их концентрации и зависит
потенциал электрода. Очевидно, сюда относятся электроды второго рода.

2. а) А каковы необратимые электроды и элементы? В этом случае при изменении направления тока (с помощью внешней цепи) происходит не та реакция, которая обратна исходной, а другая.

б) Пример — элемент Вольта (рис. 15.5):

В нем цинковая и медная пластинки погружены в один и тот же раствор.

I . При отсутствии внешней ЭДС (рис. 15.5,а) происходят те же реакции, что в элементе Даниэля–Якоби:

т.е. цинковая пластинка растворяется, а медная — утолщается. Но если изменить направление тока (рис. 15.5,б), будет происходить электролиз, и на цинковой пластинке будет выделяться не цинк, а медь — потому что сродство к электронам у неё выше, чем у цинка.

3. Наконец, отметим еще одно подразделение гальванических элементов:
с переносом и без переноса.

а) В элементах с переносом есть граница между жидкими фазами полуэлементов, и поэтому при замыкании цепи происходит перенос ионов (по солевому мостику) из одной среды в другую. Сюда относится большинство известных нам элементов.

б) В элементах же без переноса нет границы между жидкими фазами. Приме-
ры — элементы Вольта (рис. 15.5, а) и Вестона (рис. 15.1).

 

 

Потенциометрия

1. Нам осталось рассмотреть последний вопрос этого раздела — измерение ЭДС гальванических элементов в целях физико-химического анализа. Данный подход обозначается как потенциометрия. Возможные его применения весьма многообразны.

а) Например, найдя для OB-реакции ∆Ψ_рц (при нескольких температурах), можно рассчитать термодинамические параметры этой реакции — ∆G_рц, ∆G⁰_рц, K_p, ∆Н⁰_рц и ∆S⁰_рц.

б) С помощью потенциометрии определяют также характеристики растворенного вещества:

- коэффициент активности сильного электролита (активность рассчитывают по формуле Нернста и сравнивают с реальной концентрацией), 

- рН раствора и

- константу кислотности слабого электролита (в эквимолярной буферной
смеси, составленной с участием этого электролита,  рН совпадает с pK_a), и т.д.

2. Подробней остановимся на потенциометрическом титровании.

а) Это метод, используемый для определения концентрации какого-либо вещества (электролита). – Составляют гальванический элемент; в полуэлемент с исследуемым раствором последовательно добавляют титрант и измеряют каждый раз ЭДС элемента.

б) В критической точке титрования происходит резкое изменение ЭДС.

 

3. Пример: титрование раствора FeCl₃ раствором SnCl_2.

а) Пусть требуется определить в растворе концентрацию соли FeCl₃. Составим гальванический элемент (рис. 15.6): один электрод водородный, другой — редокс-электрод с изучаемым раствором FeCl₃.

б) В принципе, некоторое количество ионов Fe³⁺ могло бы восстанавливаться за счет окисления H₂. Но из-за высокого сопротивления во внешней цепи этот процесс совершенно незначителен. Поэтому до титрования в левом полуэлементе ОВ-пары ещё нет, так как имеется только один ее компонент — ионы Fe³⁺.

в) Начнем добавлять к раствору FeCl₃ в данном полуэлементе раствор соли SnCl₂ . Будет происходить реакция:

 

Поскольку появятся ионы Fe²⁺, то образуется пара Fe³⁺/Fe²⁺, и измеряемая ЭДС будет определяться соотношением её компонентов:

г) А. По мере добавления  SnCl₂  отношение c(Fe³⁺)/c(Fe²⁺)  и, следовательно, ЭДС будет снижаться (ветвь I  на рис. 15.7).

Б. В критической точке титрования (КТТ) будет оттитровано всё количество Fe³⁺, так что в растворе останутся только продукты реакции – ионы Fe²⁺ и Sn⁴⁺, т.е. ОВ-пары в растворе вновь больше нет. Но определить прохождение системой КТТ можно лишь после дальнейшего титрования.

д) А. Действительно, при добавлении очередных порций раствора SnCl₂ в системе возникнет новая ОВ пара – Sn⁴⁺/Sn²⁺, и теперь ЭДС определяется ею (ветвь II  на рис. 15.7):

 

Б. По мере добавления SnCl₂ соотношение c(Fe³⁺)/c(Fe²⁺)  тоже падает, так что ΔΨ  продолжает снижаться.

е) Но теперь критический объём титрования (V_КТТ) легко определить по точке перегиба кривой – от ветви I к ветви II. Тогда, зная количество соли в этом объёме, можно найти и количество исчезнувшей соли FeCl­­­₃ (оно в 2 раза больше), а значит и концентрацию FeCl­­­₃  в исходном растворе.

ж) Кроме того, можно оценить и стандартные  редокс-потенциалы обеих ОВ пар, если они неизвестны. Действительно,

          

            при V₁ = 0,5 V_КТТ          ΔΨ = Ψ⁰ (Fe³⁺/Fe²⁺),                 (15.28, а-б)        

 

          а при V₁ = 2 V_КТТ           ΔΨ = Ψ⁰ (Sn⁴⁺/Sn²⁺)               (15.29, а-б)       

 

Заметим, что самомỳ критическому объёму (V_КТТ ) соответствует такое ΔΨ, которое равно среднему арифметическому значению Ψ⁰ (Fe³⁺/Fe²⁺) и Ψ⁰ (Sn⁴⁺/Sn²⁺).

Краткое содержание главы 15

В этой главе продолжалось рассмотрение гальванических элементов.

1. В частности, в обобщённом виде природу элемента записывают так:

При этом  гальванические элементы  делятся на

ХИМИЧЕСКИЕ — полуэлементы различны по природе, и

КОНЦЕНТРАЦИОННЫЕ — оба полуэлемента одинаковы по природе, но различаются по концентрации компонентов.

Сами же электроды (полуэлементы) подразделяют на 4 группы.

I . ЭЛЕКТРОДЫ ПЕРВОГО РОДА – M│M²⁺, включают ПРОСТОЕ ВЕЩЕСТВО И ПРОСТОЙ ИОН этого вещества.

Примеры: электроды элемента Даниэля–Якоби — Zn│Zn²⁺ и Cu│Cu²⁺, водородный электрод — (Pt)H⁺│H, амальгамный электрод в элементе Вестона — Cd(в Hg) │Cd²⁺.

II .   ЭЛЕКТРОДЫ ВТОРОГО РОДА — КатАн↓| M |Ан. Здесь — три компонента:
ПРОСТОЕ ВЕЩЕСТВО (М), его ТРУДНОРАСТВОРИМАЯ СОЛЬ (КатАн), а также
РАСТВОРИМЫЙ ИОН данной соли (Ан). Примеры: ртутно–сульфатный электрод
элемента Вестона — Hg₂SO₄|Hg|SO₄^2-, каломельный электрод — Hg₂Cl₂|Hg(Pt)Cl^-, хлорсеребряный электрод — AgCl|Ag|Cl^-.

III . РЕДОКС-ЭЛЕКТРОДЫ: все компоненты полуреакции (Ох и Rd) находятся в растворе.

Примеры: пара 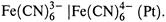, хингидронный электрод — эквимолярная смесь хинона и гидрохинона.

IV. ИОНОСЕЛЕКТИВНЫЕ ЭЛЕКТРОДЫ: включают твердую фазу, которая избирательно сорбирует из раствора те или иные ионы. Пример — СТЕКЛЯННЫЙ электрод, используемый для измерения рН.

4. Кроме того, электроды могут быть ОБРАТИМЫМИ по катиону или аниону.
Обратимыми являются  и составленные из них элементы.

НЕОБРАТИМЫЕ же элементы таковы, что при изменении направления тока происходит не реакция, обратная исходной, а другая. Пример — элемент Вольта:

                                           (-)Zn|CuSO₄|Cu(+).

5. Наконец, элементы делят еще по-иному: С ПЕРЕНОСОМ и БЕЗ ПЕРЕНОСА. В
последнем случае нет границы между жидкими фазами (пример – тот же элемент Вольта).

6. Составление гальванических элементов и измерение их ЭДС может служить для физико-химического анализа, что обозначается как ПОТЕНЦИОМЕТРИЯ. В частности, при ПОТЕНЦИОМЕТРИЧЕСКОМ ТИТРОВАНИИ в критической точке титрования резко меняется ЭДС элемента. Это позволяет оценить концентрации веществ и стандартные редокс-потенциалы.

 

 

ЗАДАЧИ К РАЗДЕЛУ 3

1. Раствор содержит оксалат натрия, Na ₂ C ₂ O ₄  ( c ₁ = 0,1 M ), сульфат меди, С uSO ₄ ( c ₂ =0,1 М) и уксусную кислоту, СН₃СООН (с₃ = 0,01 М). Найти ионную силу раствора.

Решение

Действуем по формуле (13.2):

I = 0,5 Σ z_i² c_i = 0,5 (1²·2 c ₁ + 2²·c ₁ + 2²·c ₂ + 2²·c ₂ + 1²·α·c _{3 +} 1²·α·c ₃ ) ≈ 0,7 .     (III.1)  

                                   Na ⁺   C ₂ O ₄ ^2–       Cu ⁺    SO ₄ ^2– H ⁺ CH ₃ COO ^–  

При расчёте этой суммы двумя последними слагаемыми можно пренебречь (а значит, не рассчитывать степень диссоциации α) по двум причинам:

 - во-первых, в растворе отсутствуют основания (щёлочи), а в нейтральной и кислой среде степень диссоциации (α) уксусной кислоты очень мала (11.29,б);

- во-вторых, концентрация уксусной кислоты (c ₃) на порядок ниже концентрации остальных компонентов раствора, так что даже при большей диссоциации вклад этой кислоты в ионную силу был бы весьма мал.

 

 

2. Имеется раствор Са Cl ₂ c концентрацией с = 0,002 М при 25^оС. Оценить коэффициент активности ионов Са²⁺ с помощью предельного закона Дебая-Хюккеля. Фигурирующий в этом законе коэффициент считать равным А ≈ 0,52 √1/M.  

Решение

а) Ионная сила раствора:

                                                       I = 0,5 (2²·c + 1²·2 c ) = 0,006 М .                                (III.2)

Первый член в этой сумме относится к ионам Са²⁺, второй – к ионам С l ^– .

б) Для оценки коэффициента активности ионов Са²⁺ используем формулу (13.15):       

         lg γ (Са²⁺) ≈ – A·Z (Са²⁺)²·√ I ≈ – 0,52 √1/М ·2² · √0,006 М ≈ –0,161;          (III.3,a)    

 

                                                   γ (Са²⁺) = 10^–0,161 ≈ 0,690 .                                      (III.3,б)

Как видно, даже в таком относительно разбавленном растворе (0,002 М) коэффициент активности ионов существенно меньше единицы. Правда, при использовании более точной формулы расчёта (13.16) результат оказывается несколько выше (13.18,а-б).

 

 

3. Требуется приготовить V = 1 л натрий-фосфатного буфера с рН =6,6  и ионной силой I = 0,1. Определить количество необходимых (не считая воды) компонентов (в молях). Значения рК_а для фосфорной кислоты таковы (рис. 12.2):

                        рК_а,1  = 2,1 ;   рК_а.2 = 7,2 ; рК_а.3 = 12,4 .

Решение

а) Заданное значение рН (6,23) лежит во второй буферной зоне фосфорной кислоты, в которой существуют следующие две её формы:

                                           Н₂РО₄^– ↔ Н⁺ + НРО₄^2– , рК_а.2 = 7,2   .                  (III.4)

                                      (“кислота”)               (“соль”)   

 

Таким образом, требуются две натриевые соли: Na Н₂РО₄ (“кислота”) и Na ₂ НРО₄ (“соль”).

б) Соотношение, в котором они должны быть взяты, находим из уравнения Гендерсона-Хассельбаха (12.3):

         рН = рК_а.2 + lg (с_с /с_к ),  откуда lg (с_с /с_к ) = – 0,6 и с_с /с_к ≈ 0,25 .  (III.5,а-в)

в) Количество же солей определяется условием, наложенным на ионную силу:

 

           I (моль/л) = 0,5 ( 1²·2 c _с + 1²·c _к + 2²·c _с + 1²·c _к ) = 0,1.            (III.6,а)                     

                     

                                Na⁺ из “соли” Na⁺ из “к-ты” HPO₄^2– H₂PO₄^–      

Отсюда

                                                  3 c _с + c _к = 0,1 моль/л                                                 (III.6,б)

г) Подставляя в это уравнение с_с = 0,25 с_к (из III.5,в), легко находим искомые концентрации компонентов в составляемой буферной системе:

                                             с_к   ≈ 0,057 моль/л ; с_с   ≈ 0,014 моль/л .                     (III.7,а)

Поскольку требуемый объём раствора – 1 л , то таковы же по величине и количества солей, необходимые для приготовления системы:

                     n ( Na Н₂РО₄) = 0,057 молей и n ( Na ₂ НРО₄)= 0,014 молей .             (III.7,б)