Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Теперь перейдём к влиянию концентрации на электропроводность.

1. В п.13.5 говорилось, что с ростом концентрации электролита взаимодействие ионов увеличивается, и поэтому эквивалентная проводимость снижается.

В качестве конкретных причин можно назвать два эффекта. Причём оба они связаны с оболочкой из противоионов, которая, согласно теории Дебая и Хюккеля, в достаточно концентрированном растворе существует вокруг каждого иона (п. 13.2).

2. а) Электрофоретический эффект: указанная оболочка стремится перемещаться в противоположную сторону, что замедляет движение центрального иона.

б) Релаксационный эффект: в процессе своего перемещения оболочка деформируется, так что с одной стороны от центрального иона создается избыток отрицательных зарядов, а с другой стороны — дефицит. Следовательно, возникает поле, ослабляющее внешнее поле.

 3. а) Примерный вид зависимости эквивалентной проводимости от концентрации
показан на чертеже (рис. 13.4, а).

б) Экстраполяция к нулевой концентра-ции (т.е. к бесконечному разбавлению раствора) позволяет определить предельные значения эквивалентной проводимости, а значит и связанных с ней подвижностей ионов:

в) Именно данные величины и приводятся в справочниках, что нашло отражение в табл. 13.1. (Иногда для них используются обозначения ).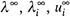

4. а) При конечных же концентрациях проводимость раствора и подвижность
ионов меньше предельных значений.

б) Это отличие характеризуется коэффициентом электрической проводимости:

 

5. Относительно введённого коэффициента следует сделать три замечания.

а) Для чистого раствора слабого электролита (при с » К_а) f_λ  практически равен 1. Поэтому подвижность ионов в широком диапазоне концентраций близка к предельной, но эквивалентная проводимость раствора ниже предельной:

 

                 λ _i ≈ λ _i⁰ ,    λ = α∙Σ λ _i ≈ α∙Σ λ _i⁰ = α∙λ⁰  < λ⁰                 (13.50)

                                          

В растворе же сильного электролита, как следует из (13.49), ниже предельных значений являются и подвижность ионов, и итоговая проводимость:

 

         λ _i  = f_λ ∙ λ _i⁰ ,    λ = Σ λ _i ≈ f_λ ∙ Σ λ _i ⁰ = f_λ ∙ λ⁰ .              (13.51,а)

б) Коэффициент f_λ (для сильных электролитов), равно как и степень диссоциации α  (для слабых электролитов), зависит от концентрации раствора, уменьшаясь с её ростом.

в) Наконец, в бесконечно разбавленных растворах

    f_λ → 1, α → 1 (11.26,в),  откуда  λ⁰ = Σ λ _i⁰ .                 (13.51,б)

 

Заключённое в рамку уравнение аналогично уравнению (13.41,а), но трактуется как выражение закона Кольрауша:  в бесконечно разбавленном растворе ионы движутся независимо друг от друга. 

6. Конкретная зависимость эквивалентной проводимости от концентрации
приближенно описывается уравнением Онзагера.

а) Если электролит диссоциирует только на одновалентные ионы, то данное
уравнение таково:

Здесь член B₁λ⁰ учитывает релаксационный эффект, а член В₂ — электрофоретический эффект торможения. 

б) Уравнение описывает линейное снижение λ по мере роста 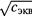. Для сильных электролитов это справедливо на достаточно большом интервале концентрации (рис. 13.5).

7. Коротко — о зависимости удельной проводимости χ  от концентрации.

а) В п. 13.5 отмечалось, что на данную величину концентрация раствора оказывает два противоположных влияния. И действительно, согласно (13.30), удельная проводимость есть произведение двух величин —

 

б) За счет первого сомножителя проводимость с увеличением концентрации
вначале растет. Затем же, когда начинает преобладать снижение λ, удельная
проводимость начинает уменьшаться.

Так что зависимость χ(c_экв) является двухфазной (рис. 13.4,5).

 

Кондуктометрия

После рассмотрения основ электропроводности растворов кратко остановимся на использовании этого явления в целях физико-химического анализа.

а) Измерение электропроводности раствора электролита называется кондуктометрией (от англ. « to conduct » — проводить).

б) Для подобных измерений созданы специальные приборы — кондуктометры.

В основе их — схема из четырех сопротивлений — мост Уитстона (рис. 13.6). Исследуемый раствор помещают в кондуктометрическую ячейку, после чего этот раствор служит одним из сопротивлений схемы, а именно, сопротивлением R_χ.

Еще одно сопротивление является переменнным (R_упр). Изменяя его, добиваются того, чтобы разность потенциалов между точками А и В обратилась в нуль.

в) Тогда выполняются соотношения:

 

откуда измеряемое сопротивление равно

г) Зная его и параметры ячейки ( l , S ), по формулам (13.28—13.30) нетрудно найти удельную и эквивалентную электропроводность:

 

Из многих применений кондуктометрии отметим лишь два.

1. Определение степени и константы диссоциации слабого электролита.

Вариант I . Для ионов, на которые диссоциирует электролит, известны
предельные эквивалентные подвижност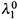и — и ^.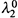

а) Исходя из формулы (13.50), получаем:

б) Следовательно, определив экспериментально λ, можно оценить степень
диссоциации слабого электролита при данной его концентрации.

в) А зная α — с помощью закона разведения Оствальда рассчитать и кон-
станту диссоциации:

 

Вариант II . Величины 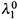и 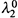неизвестны. Как в этом случае найти α  и K_a?

а) Соотношение (13.56, а) можно записать и так:

где λ⁰— предельная эквивалентная проводимость раствора. Подставляем его
в (11.25):

б) Последнее уравнение преобразуем к виду:

что после деления на λ дает:

В итоге получается линейная зависимость χ (удельной электропроводности) от 1/λ (рис. 13.7).

в) Следовательно, если по экспериментальным данным построить график такой зависимости, то по точке его пересечения с осью абсцисс можно найти 1/λº, затем для какой-либо концентрации — α (по формуле (13.56,6)) и, наконец, K_a (11.25).

г) Что касается K_a, то можно воспользоваться и указанным графиком:

 

2. Кондуктометрическое титрование.

а) А этот метод применяется для определения концентрации веществ. Принцип основан на том, что в т.н. критических точках титрования (КТТ) резко меняется зависимость проводимости раствора от количества титранта. Три примера кривых титрования приведены на рис. 13.8.

 

б) Чтобы объяснить первую кривую, обратимся к реакции

I . При добавлении в ячейку NaOH подвижные ионы H⁺ связываются с
гидроксил–ионами и заменяются на менее подвижные ионы Na⁺. Поэтому электропроводность ячейки снижается и в критической точке титрования (V_KTT)
она минимальна.

II . Но затем, по мере добавления избыточных количеств ионов Na⁺ и OH^-, которые уже ни с чем не связываются и ничего не замещают, а просто накапливаются в ячейке, электропроводность, очевидно, опять повышается.

в) При титровании слабого электролита (рис. 13.8,б) небольшой подъем χ наблюдается задолго до V_KTT — из-за того, что увеличивается степень диссоциации электролита. Но после V_KTT  проводимость начинает возрастать гораздо быстрей.

 

Краткое содержание главы 13

 

Глава посвящена РАСТВОРАМ СИЛЬНЫХ ЭЛЕКТРОЛИТОВ.

1. Так, было введено понятие ИОННОЙ СИЛЫ раствора:

      I ≡ 0,5 Σ c_i·z_i² .

2. От этой величины зависит, в частности, КОЭФФИЦИЕНТ АКТИВНОСТИ любого электролита, присутствующего в растворе. Зависимость описывается ФОРМУЛОЙ ДЕБАЯ-ХЮККЕЛЯ, которая имеет три варианта – в том числе

 

 

Соответствующие графики изображены на рисунке.

Другая рассмотренная проблема – ПРОВЕДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА растворами электролитов.

3. а) Введены две характеристики движения ионов i-того вида – ПОДВИЖНОСТЬ (u_i) и ЭКВИВАЛЕНТНАЯ ПОДВИЖНОСТЬ (λ _i):          

                          u_i  ≡ v_дв,i / E , м²/( B∙c ) ;        λ _i ≡ u_i∙F , м²∙C м/моль.

Определены также две характеристики электропроводности раствора – УДЕЛЬНАЯ ПРОВОДИМОСТЬ ( χ) и ЭКВИВАЛЕНТНАЯ ПРОВОДИМОСТЬ (λ):

                       χ ≡ 1 / ρ , См / м ;             λ ≡ χ / c _экв , м²∙C м/моль.

б) Установлена взаимосвязь между подвижностью ионов и проводимостью раствора:

                                 λ = Σ λ _i ,                 λ = α∙Σ λ _i

(второе соотношение – для раствора слабого электролитов).

4. Рассмотрены факторы, влияющие на введённые характеристики.

а) Для сферических заряженных частиц при предельном разбавлении справедлива формула:

                                        u_{i ,сф} = Z_i e / (6 πη r_i ) .

Согласно ей, на подвижность частиц влияют их ЗАРЯД, РАЗМЕР, а также ВЯЗКОСТЬ среды.

б) Немаловажную роль имеет ФОРМА частиц, МЕХАНИЗМ их ПЕРЕМЕЩЕНИЯ, ТЕМПЕРАТУРА и КОНЦЕНТРАЦИЯ раствора. В частности, с ростом концентрации эквивалентная проводимость 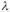снижается, что отражается эмпирическим УРАВНЕНИЕМ ОНЗАГЕРА:

в) И лишь в бесконечно разбавленном растворе ионы движутся независимо друг от друга (ЗАКОН КОЛЬРАУША):

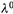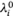где  и  — предельные значения проводимости раствора и подвижностей, ионов,
достигаемые при c_экв →0.

5. На измерении электропроводности раствора основана КОНДУКТОМЕТРИЯ – метод физико-химического анализа. Так, при КОНДУКТОМЕТРИЧЕСКОМ ТИТРОВАНИИ в критической точке  титрования резко меняется зависимость электропроводности от количества титранта.