У багатьох задачах потрібно встановити й оцінити залежність досліджуваної випадкової величини Y від однієї або декількох інших випадкових величин. Роздивимося залежність Y від однієї випадкової величини Х. Строга функціональна залежність реалізується рідко, тому що обидві величини або одна з них підлягає дії випадкових чинників. У цьому випадку виникає статистична залежність. Зокрема, статистична залежність виявляється в тому, що при зміні однієї з величин змінюється середнє значення іншої; у цьому випадку статистичну залежність називають кореляційною.
Основна задача регресійного аналізу – визначення форми й параметрів рівняння зв'язку між змінними. Основна задача кореляційного аналізу – визначення зв'язку між випадковими змінними й оцінка його тісноти.
Схематично аналіз зв'язку між змінними можна розділити на наступні етапи:
1. Постановка задачі, встановлення наявності зв'язку між досліджуваними змінними.
2. Визначення характеру зв'язку, його напрямку й форми, підбір математичного рівняння для вираження існуючого зв'язку (за допомогою побудови графіків (кореляційного поля та ін), складання кореляційних таблиць, перегляду різних функцій тощо).
3. Розрахунок числових характеристик кореляційного зв'язку (визначення параметрів рівняння і показників тісноти зв'язку).
4. Статистична оцінка (перевірка значущості) вибіркових показників зв'язку (за допомогою відповідних критеріїв перевірки статистичних гіпотез).
5. Розрахунок прогнозних значень залежної змінної при відповідних значеннях незалежних змінних (факторів).
Припустимо, що вивчається зв'язок між випадковою величиною Y і випадковою величиною Х . Нехай кожному значенню Х відповідає декілька значень Y.
Умовним середнім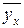 
називають середнє арифметичне значення Y, що відповідає значенню Х = х.
Кореляційною залежністю Y від Х називають функціональну залежність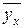 
від х:
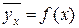
Це рівняння називають рівнянням регресії Y на X; функцію f(x) регресією Y на Х, а її графік – лінією регресії Y на Х .
Припустимо, що ознаки Y і Х пов'язані лінійною кореляційною залежністю. У цьому випадку лінії регресії будуть прямими.
Припустимо, що для опису рівнянь цієї прямій проведено п незалежних іспитів, у результаті яких отриманий пар чисел: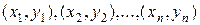 
. Рівняння, знайдені за цими даними, називають вибірковими.
Будемо шукати вибіркове рівняння прямої лінії регресії Y на Х . Для цього введемо поняття вибіркового коефіцієнта кореляції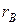 
. Він визначається співвідношенням:
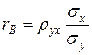(3.1)
де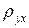 
- коефіцієнт регресії, рівний
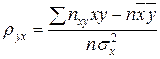
де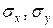 
- середньоквадратичні відхилення випадкових величин Х і Y відповідно.
Одержимо формулу для вибіркового коефіцієнта кореляції
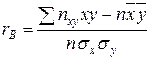
де х, у – варіанти (значення), що спостерігалися;
п xy – частота пари (х,у) варіант, що спостерігалася;
n - обсяг вибірки;
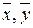– вибіркові середні;
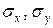– вибіркові середні квадратичні відхилення.
Властивості коефіцієнтом кореляції:
Коефіцієнт кореляції приймає значення на відрізку [-1;1], тобто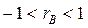 
.
Чим ближче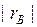 
до 1, тим тісніший зв'язок, тим ближче точки кореляційного поля відстають від прямої лінії регресії (розрізняють зв'язок слабкий, помірний, помітний, достатньо тісний, тісний і дуже тісний). Знак при коефіцієнті кореляції вказує на напрямок зв'язку ("+"– прямий, "–" – зворотний).
При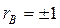 
кореляційний зв'язок представляє лінійну функціональну залежність. Точки кореляційного поля знаходяться на прямій лінії.
При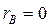 
лінійний кореляційний зв'язок відсутній. При цьому може бути нелінійна кореляційна або статистична залежність.
Вибірковий коефіцієнт кореляції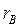 
є оцінкою коефіцієнта кореляції генеральної сукупності (тим більше точною, чим більше об'єм вибірки n).
Квадрат коефіцієнта кореляції називається коефіцієнтом детермінації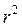 
. Він показує, яка доля загальної варіації залежної змінної у визначається фактором х. Якщо коефіцієнт детермінації виражається у відсотках, то він показує, на скільки відсотків варіація (коливання) залежної змінної у обумовлена варіацією факторах.
Коефіцієнт детермінації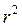 
приймає значення на відрізку [0;1]. Чим ближче 
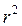до 1, тим тісніший зв'язок між змінними.
Вибіркове рівняння прямої лінії регресії Y на Х можна записати у виді :
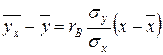
або
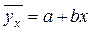
де
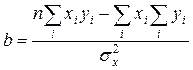
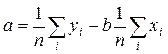
ПРИКЛАД 10. На 100 ділянках землі площею 0,3 га (кожна з різною кількістю внесених добрив) зроблено обстеження урожайності кукурудзи. Результати наведені в таблиці.
Таблиця 15
| Зібрано зерна с ділянки, ц | Кількість добрив, внесених на делянку, т | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 14 | 10 | 8 | – | – | – |
| 15 | – | 12 | 7 | – | – |
| 16 | – | – | 28 | 6 | – |
| 17 | – | – | – | 8 | 9 |
| 18 | – | – | – | – | 12 |
На підставі цих даних знайти: а) вибіркове рівняння лінійної регресії, що описує кореляційну залежність величини урожайності (у) від кількості внесених добрив (x); б) вибіркові коефіцієнти кореляції і детермінації.
РОЗВ’ЯЗАННЯ. Складемо кореляційну таблицю (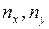 
– частоти значень x і y відповідно, n – об’єм вибірки).
| y | x | ny | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| 14 | 10 | 8 | – | – | – | 18 |
| 15 | – | 12 | 7 | – | – | 19 |
| 16 | – | – | 28 | 6 | – | 34 |
| 17 | – | – | – | 8 | 9 | 17 |
| 18 | – | – | – | – | 12 | 12 |
| nx | 10 | 20 | 35 | 14 | 21 | 
|
Знайдемо середні.
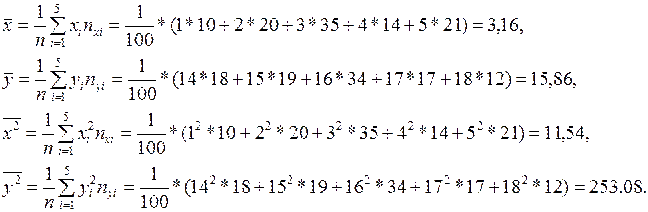
Обчислимо вибіркові дисперсії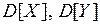 
, а потім вибіркові середньоквадратичні відхилення 
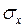і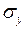 
.
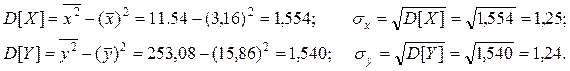
Знайдемо параметри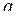 
і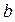 
рівняння лінійної регресії
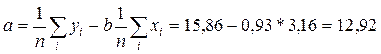
Отже рівняння лінійної регресії
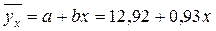
Коефіцієнт регресії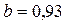 
показує, що при збільшенні кількості внесених добрів (x) на одну тону урожайність кукурудзи (y) в середньому збільшується на 0,93 т.
Розрахуємо вибірковий лінійний коефіцієнт кореляції
.
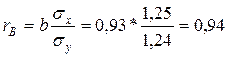Коефіцієнт кореляції показує, що між урожайністю і кількістю внесених добрів існує дуже тісний зв’язок.
Коефіцієнт детермінації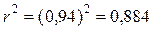 
показує, що 88,4% загальної варіації урожайності обумовлено кількістю внесених добрів, решта (11,6%) – іншими факторами, які в даній задачі не були враховані.
КОНТРОЛЬНА РОБОТА
ЗАДАЧА 1. Задано вибірку, що отримана для дискретної випадкової величини. Обробивши її, побудувати:
1) варіаційний ряд;
2) статистичний розподіл вибірок у частотах і відносних частотах;
3) полігон частот;
4) знайти чисельні характеристики вибірки:
· вибіркову середню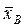 
· статистичні моду Мо і медіану Ме
· статистичні дисперсію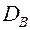 
і середньоквадратичне відхилення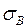 
№1
| 12 6 8 10 4 9 8 12 9 12 8 7 14 7 16 5 11 7 4 5 8 5 8 4 7 9 9 6 9 5 |
№2
| 2 4 8 5 9 3 5 9 4 10 15 9 5 10 5 7 7 12 8 6 13 9 5 11 9 13 11 12 8 4 |
№3
| 5 10 7 7 8 10 13 7 10 5 7 10 10 11 9 16 12 10 7 5 13 7 12 6 13 12 13 12 8 14 |
№4
| 13 19 8 12 15 15 13 12 17 13 17 15 19 14 13 15 13 18 13 8 8 9 14 16 9 14 19 15 12 11 |
№5
| 8 10 8 8 7 5 3 6 9 6 9 8 8 4 15 5 7 4 10 10 5 3 6 11 7 6 9 8 11 11 |
№6
| 3 0 1 1 2 2 2 0 1 1 1 1 0 4 3 1 1 3 3 1 2 1 1 3 4 3 3 2 2 2 |
№7
| 2 3 1 4 3 1 1 2 1 2 3 4 1 4 3 5 3 4 1 2 5 4 2 4 4 3 3 4 5 4 |
№8
| 2 2 1 1 3 1 3 2 0 2 3 3 2 1 1 2 2 3 2 2 2 2 2 3 2 3 2 2 3 3 |
№9
| 3 2 3 4 2 2 2 3 2 1 3 1 2 2 2 1 2 1 4 2 3 3 3 1 1 2 4 2 3 2 |
№10
| 3 2 1 3 1 2 1 1 4 2 1 3 3 4 2 2 2 4 3 1 1 4 3 3 1 0 3 2 3 4 |
ЗАДАЧА 2. Задано вибірку, отримана для безупинної випадкової величини, Обробивши її, побудувати:
1) варіаційний ряд.
2) виконати інтервальну угруповання даних.
3) побудувати гістограму відносних частот.
4) знайти чисельні характеристики вибірки:
· вибіркову середню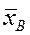 
· статистичні моду Мо і медіану Ме
· статистичні дисперсію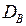 
і середньоквадратичне відхилення .
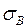№1
| 1,65 7,86 6,96 4,95 1,88 0,23 0,39 5,16 0,71 5,56 0,73 23,92 3,01 6,79 3,49 1,11 8,72 24,08 0,62 2,06 7,93 4,96 6,67 2,57 0,98 12,32 1,65 3,03 7,32 0,42 |
№2
| 7,43 6,44 17,77 7,74 19,52 5,97 4,75 31,92 4,27 39,68 1,37 17,13 3,31 0,55 1,01 6,83 1,31 6,45 0,69 3,56 9,15 9,89 2,10 9,46 1,67 0,08 0,44 6,25 0,90 9,30 |
№3
| 0,16 0,77 6,57 0,61 9,10 26,43 6,73 0,86 8,44 0,91 2,56 3,41 13,74 3,99 1,77 18,34 6,16 1,01 11,63 6,86 19,76 12,44 14,18 4,78 0,53 0,42 5,83 1,85 1,92 3,17 |
№4
| 12,93 26,27 3,21 11,19 0,87 4,66 11,37 14,37 18,65 10,07 50,78 19,96 12,64 3,04 0,73 16,04 2,81 23,90 1,74 27,30 20,94 28,65 22,97 6,65 35,39 5,19 24,64 0,31 2,60 9,54 |
№5
| 12,88 8,71 9,64 12,31 10,26 12,48 17,49 4,42 4,65 14,71 10,15 11,69 7,42 20,38 13,61 8,60 9,68 10,92 15,35 7,08 6,05 21,58 5,39 9,87 14,28 6,23 8,94 19,51 3,61 10,18 |
№6
| 0,40 1,75 0,47 1,57 2,07 0,73 3,86 5,27 0,43 2,25 2,05 1,50 1,23 3,67 1,34 1,54 2,49 1,15 0,67 1,31 1,95 1,77 0,50 0,49 0,40 1,94 0,91 8,60 1,91 3,59 |
№7
| 1,50 0,93 1,40 0,41 0,54 0,47 5,19 1,04 0,31 1,56 0,52 0,61 2,04 1,15 1,20 1,43 0,71 1,32 0,90 0,72 0,85 0,56 1,98 0,50 0,71 0,32 0,38 0,36 0,56 2,17 1,44 |
№8
| -3,29 0,18 4,02 11,38 5,74 9,11 11,17 0,44 9,79 -0,27 -5,55 2,37 6,66 -2,12 3,99 0,67 -1,74 3,69 1,65 3,61 7,72 5,13 5,87 8,62 1,39 4,00 1,67 3,37 7,29 0,62 |
№9
| 3,63 9,34 15,16 -6,46 -13,19 -7,92 7,06 12,34 14,46 -15,45 11,51 1,62 15,04 -7,90 -6,04 8,35 11,70 4,69 -3,47 0,44 -4,24 3,57 14,35 7,89 5,56 14,43 5,56 6,76 -4,17 3,01 |
№10
| -5,52 13,13 -14,81 21,07 13,98 8,87 -0,63 9,14 7,35 -2,35 5,98 16,67 13,92 21,64 0,18 -0,62 8,72 13,94 2,72 13,74 -0,96 18,34 7,88 0,13 -8,66 16,50 27,44 -6,34 -0,34 18,58 |
ЗАДАЧА 3. Задано вибірку, Необхідно:
1) побудувати статистичну функцію розподілу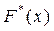 
. Записати її аналітичне вираження. Побудувати графік.
2) виконати інтервальну оцінку параметрів розподілу:
· Математичного сподівання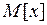 
,
· Середньоквадратичного відхилення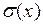 
(Довірчу імовірність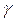 
прийняти рівної 0,95)
№1
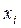
| 2 | 5 | 7 | 9 | 11 | 13 | 17 |
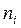
| 11 | 15 | 9 | 13 | 25 | 17 | 10 |
№2
|
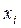
| 12 | 14 | 18 | 21 | 25 | 27 | 31 |
| 10 | 15 | 22 | 31 | 24 | 14 | 9 |
№3
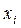
| 1 | 3 | 7 | 9 | 11 | 14 | 21 |
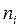
| 36 | 32 | 21 | 19 | 15 | 22 | 34 |
№4
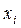
| 3 | 5 | 6 | 8 | 11 | 12 | 15 |
|
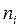
| 22 | 31 | 24 | 23 | 28 | 32 | 19 |
№5
|
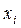
| 2 | 5 | 7 | 9 | 13 | 16 | 18 |
|
| 18 | 14 | 13 | 19 | 22 | 34 | 45 |
№6
|
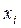
| 1 | 4 | 5 | 8 | 10 | 13 | 15 |
|
| 34 | 43 | 25 | 29 | 34 | 28 | 30 |
№7
|
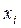
| 4 | 5 | 7 | 8 | 9 | 11 | 13 |
|
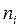
| 21 | 23 | 24 | 19 | 17 | 22 | 25 |
№8
|
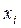
| 4 | 6 | 8 | 12 | 14 | 15 | 17 |
|
| 11 | 12 | 9 | 16 | 19 | 21 | 15 |
№9
|
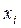
| 1 | 3 | 5 | 9 | 11 | 14 | 17 |
|
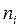
| 24 | 25 | 33 | 21 | 17 | 15 | 22 |
№10
|
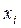
| 2 | 3 | 4 | 6 | 7 | 9 | 10 |
|
| 34 | 31 | 27 | 24 | 22 | 17 | 13 |
ЗАДАЧА 4. Задано вибірку, отримана для безупинної випадкової величини X. Обробивши її, записати гіпотезу про вид закону розподілу. Перевірити гіпотезу, використовуючи критерій Пірсона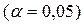 
№1.
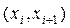
| (2;4) | (4;6) | (6;8) | (8;10) | (10;12) | (12;14) | (14;16) |
|
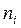
| 49 | 35 | 24 | 17 | 9 | 5 | 1 |
№2.
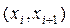
| (0;3) | (3;6) | (6;9) | (9;12) | (12;15) | (15;18) | (18;21) |
|
| 13 | 8 | 12 | 10 | 9 | 11 | 10 |
№3.
|
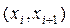
| (0;5) | (5;10) | (10;15) | (15;20) | (20;25) | (25;30) | (30;35) |
|
| 2 | 16 | 34 | 35 | 31 | 13 | 1 |
№4.
|
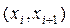
| (1;3) | (3;5) | (5;7) | (7;9) | (9;11) | (11;13) | (13;16) |
|
| 65 | 50 | 37 | 21 | 12 | 4 | 2 |
№5.
|
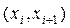
| (0;4) | (4;8) | (8;12) | (12;16) | (16;20) | (20;24) | (24;28) |
|
| 37 | 43 | 34 | 41 | 45 | 39 | 42 |
№6.
|
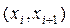
| (-1;1) | (1;3) | (3;5) | (5;7) | (7;9) | (9;11) | (11;13) |
|
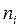
| 4 | 12 | 24 | 37 | 19 | 9 | 2 |
№7.
|
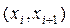
| (-6;-3) | (-3;0) | (0;3) | (3;6) | (6;9) | (9;12) | (12;15) |
|
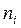
| 44 | 25 | 18 | 11 | 4 | 2 | 1 |
№8.
|
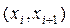
| (-5;-1) | (-1;3) | (3;7) | (7;11) | (11;15) | (15;19) | (19;23) |
|
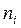
| 4 | 16 | 28 | 35 | 31 | 19 | 6 |
№9.
|
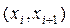
| (2;4) | (4;6) | (6;8) | (8;10) | (10;12) | (12;14) | (14;16) |
|
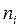
| 27 | 31 | 29 | 33 | 30 | 24 | 22 |
№10.
|
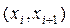
| (0;3) | (3;6) | (6;9) | (9;12) | (12;15) | (15;18) | (18;21) |
|
| 3 | 8 | 22 | 43 | 29 | 11 | 5 |
ЗАДАЧА 5. Задано вибірку, що отримана для дискретної випадкової величини X. Перевірити гіпотезу про вид закону розподілу, використовуючи критерій Пірсона (a = 0,05).
№1. Розподіл Пуассона.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 269 | 175 | 41 | 9 | 4 | 2 |
№2. Біноміальний розподіл.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 2 | 4 | 15 | 51 | 17 | 8 |
№3. Розподіл Пуассона.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 301 | 132 | 54 | 10 | 2 | 1 |
№4. Біноміальний розподіл.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 3 | 6 | 18 | 47 | 19 | 7 |
№5. Розподіл Пуассона.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 285 | 144 | 39 | 12 | 4 | 2 |
№6. Біноміальний розподіл.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 6 | 11 | 25 | 67 | 21 | 14 |
№7. Розподіл Пуассона.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 315 | 196 | 58 | 17 | 0 | 3 |
№8. Біноміальний розподіл.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 3 | 7 | 22 | 65 | 19 | 13 |
№9. Розподіл Пуассона.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 244 | 131 | 55 | 19 | 7 | 4 |
№10. Біноміальний розподіл.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 3 | 7 | 22 | 64 | 19 | 11 |
ЗАДАЧА 7. За даними таблиці визначити параметри емпіричного й теоретичного розподілів і за допомогою критерію Колмогорова оцінити близькість емпіричного розподілу до нормального.
№1.
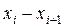
| 110- 115 | 115- 120 | 120- 125 | 125-130 | 130-135 | 135- 140 | 140- 145 | 145- 150 | 150-155 |
|
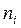
| 20 | 62 | 144 | 170 | 188 | 176 | 124 | 74 | 24 |
№2.
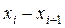
| 0- 20 | 20- 40 | 40- 60 | 60- 80 | 80- 100 | 100- 120 | 120- 140 | 140- 160 | 160- 180 |
|
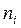
| 30 | 80 | 200 | 400 | 470 | 360 | 180 | 50 | 25 |
№3.
|
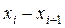
| 6,65- 6,70 | 6,70- 6,75 | 6,75- 6,80 | 6,80- 6,85 | 6,85- 6,90 | 6,90- 6,95 | 6,95- 7,00 | 7,00- 7,05 | 7,05- 7,10 |
|
| 5 | 17 | 24 | 54 | 52 | 23 | 18 | 7 | 4 |
№4.
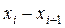
| 3,0- 3,6 | 3,6- 4,2 | 4,2- 4,8 | 4,8- 5,4 | 5,4 6,0 | 6,0- 6,6 | 6,6- 7,2 | 7,2- 7,8 | 7,8- 8,4 |
|
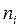
| 2 | 8 | 35 | 43 | 22 | 15 | 5 | 4 | 2 |
№5.
|
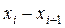
| 5- 10 | 10- 15 | 15- 20 | 20- 25 | 25- 30 | 30- 35 | 35- 40 | 40- 45 | 45- 50 |
|
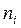
| 7 | 8 | 15 | 18 | 19 | 14 | 10 | 6 | 3 |
№6.
|
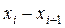
| 2- 4 | 4- 6 | 6- 8 | 8- 10 | 10- 12 | 12- 14 | 14- 16 | 16- 18 | 18- 20 |
|
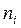
| 5 | 15 | 25 | 30 | 50 | 28 | 30 | 20 | 7 |
№7.
|
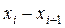
| 125- 175 | 175- 225 | 225- 275 | 275- 325 | 325- 375 | 375- 425 | 425- 475 | 475- 525 | 525- 575 |
|
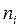
| 12 | 24 | 28 | 28 | 20 | 16 | 15 | 12 | 12 |
№8.
|
| 2- 5 | 5- 8 | 8- 11 | 11- 14 | 14- 17 | 17- 20 | 20- 23 | 23- 26 | 26- 29 |
|
| 25 | 25 | 70 | 120 | 187 | 130 | 80 | 20 | 8 |
№9.
|
| 7- 9 | 9- 11 | 11- 13 | 13- 15 | 15- 17 | 17- 19 | 19- 21 | 21- 23 | 23- 25 |
|
| 40 | 60 | 75 | 95 | 125 | 88 | 80 | 50 | 37 |
№10.
|
| 2- 4 | 4- 6 | 6- 8 | 8- 10 | 10- 12 | 12- 14 | 14- 16 | 16- 18 | 18- 20 |
|
| 7 | 18 | 35 | 45 | 50 | 40 | 30 | 15 | 10 |
ЗАДАЧА 8. В таблицях наведено дані, що характеризують залежність змінної y від змінної x . На підставі цих даних: а) знайти вибіркове рівняння лінійної регресії, що описує кореляційну залежність y від x; б) обчислити вибіркові коефіцієнти кореляції й детермінації.
№1
| Y | X | |||||
| 4 | 9 | 14 | 19 | 24 | 29 | |
| 20 | 1 | 8 | - | - | - | - |
| 30 | - | 9 | 3 | - | - | - |
| 40 | - | 4 | 5 | 46 | - | - |
| 50 | - | - | - | 6 | 8 | - |
| 60 | - | - | - | - | 4 | 6 |
№2
| Y | X | |||||
| 10 | 15 | 20 | 25 | 30 | 35 | |
| 6 | 3 | 5 | 4 | - | - | - |
| 8 | - | 2 | 1 | 3 | - | - |
| 12 | - | 4 | 40 | 8 | - | - |
| 16 | - | - | - | 5 | 7 | 5 |
| 20 | - | - | - | - | 7 | 10 |
№3
| Y | X | |||||
| 6 | 12 | 18 | 24 | 30 | 36 | |
| 4 | 4 | 1 | 3 | - | - | - |
| 9 | - | 5 | 9 | - | - | - |
| 14 | - | - | 18 | 6 | 9 | - |
| 19 | - | - | 4 | 3 | 10 | - |
| 24 | - | - | - | - | 1 | 10 |
№4
| Y | X | |||||
| 5 | 10 | 15 | 20 | 25 | 30 | |
| 6 | 1 | 4 | - | - | - | - |
| 10 | - | 5 | 9 | - | - | - |
| 14 | - | - | 38 | 6 | 9 | - |
| 18 | - | - | 4 | 3 | 10 | - |
| 22 | - | - | - | - | 1 | 10 |
№5
| Y | X | |||||
| 8 | 14 | 20 | 26 | 32 | 38 | |
| 5 | 8 | 3 | 4 | - | - | - |
| 10 | - | - | 11 | 38 | - | - |
| 15 | - | - | 6 | 1 | 4 | - |
| 20 | - | - | - | 7 | 1 | - |
| 25 | - | - | - | - | 9 | 8 |
№6
| Y | X | |||||
| 3 | 8 | 13 | 18 | 23 | 28 | |
| 1 | 1 | 3 | 6 | - | - | - |
| 6 | - | 4 | 7 | - | - | - |
| 11 | - | - | 50 | 9 | 1 | - |
| 16 | - | - | 2 | 8 | 2 | - |
| 21 | - | - | - | 1 | 3 | 3 |
№7
| Y | X | |||||
| 7 | 10 | 13 | 16 | 19 | 22 | |
| 2 | 3 | 5 | - | - | - | - |
| 4 | - | 15 | 9 | - | - | - |
| 6 | - | - | 23 | 6 | 1 | - |
| 8 | - | - | - | 12 | 7 | - |
| 10 | - | - | - | - | 14 | 5 |
№8
| Y | X | |||||
| 2 | 7 | 12 | 17 | 22 | 27 | |
| 20 | 4 | 1 | 3 | - | - | - |
| 30 | - | 5 | 6 | - | - | - |
| 40 | - | - | 7 | 40 | 8 | - |
| 50 | - | - | - | 9 | 1 | 3 |
| 60 | - | - | - | - | 9 | 4 |
№9
| Y | X | |||||
| 10 | 20 | 30 | 40 | 50 | 60 | |
| 1 | 2 | 2 | 3 | - | - | - |
| 6 | - | 4 | 4 | 5 | - | - |
| 11 | - | - | 40 | 11 | 21 | - |
| 16 | - | - | - | 1 | 2 | 3 |
| 21 | - | - | - | - | - | 4 |
№10
| Y | X | |||||
| 1 | 4 | 7 | 10 | 13 | 16 | |
| 9 | 7 | 3 | - | - | - | - |
| 13 | - | 10 | 23 | 5 | - | - |
| 17 | - | - | 5 | 43 | 8 | - |
| 21 | - | - | - | - | 9 | 6 |
| 25 | - | - | - | - | - | 6 |
ЛІТЕРАТУРА
1. Гмурман В.Е. Теория верностей и математическая статистика. Учебн. пособие для вузов. – 7-е издание – М.: Высш. шк., 1999. – 479 с.
2. Гмурман В.Е. Руководство к решению задач по теории верностей и математической статистике. Учебн. пособие для студ. вузов. – 5-е издание – М.: Высш. шк., 2000. – 400 с.
3. Ю.Д.Заворотнев, А.С.Крахмаль, Е.Б.Лещинский. Курс лекций по вероятностно-статистическим методам в психологи / Часть 1. Основы теории вероятностей и математической статистики // Учебное пособие. – Донецк: Норд-Пресс. – 275 с.
4. Практикум з теорії ймовірностей та математичної статистики: Навч. посіб. для студ. вищ. навч. зал. / Р.К.Чорней, О.Ю.Дюженкова, О.Б.Жильцов та ін.; За ред. Р.К.Чорнея. – К.: МАУП, 2003. – 328 с.
5. Теория верностей и математическая статистика. Учебн. пособие для вузов/ Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фурман; Под ред.. проф. Н.Ш.Кремера. – М.: ЮНИТИ, 2000. – 407 с.
6. Жлуктенко B.I. Наконєчний С.І. Теорія ймовірностей із елементами математичної статистики. – К., УМКВО, 1991.
7. Жлуктенко B.I., Наконєчний C.I. Практикум з курсу "Теорія ймовірностей і математична статистика". – К.: КІНГ, 1991.
8. Заворотнєв Ю.Д., Крахмаль А.С., Маєвський B.C. Теорія ймовірностей. Навчальний посібник. Макіївка, 1996.
9. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1971.
ДОДАТОКИ
Таблиця 1. Значення функції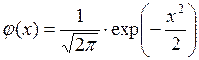 
| 
|
|
|
|
|
|
|
|
|
|
|
| 0,00 01 02 03 04 05 06 07 08 09 0,10 11 12 13 14 15 16 17 18 19 0,20 21 22 23 24 25 26 27 28 29 0,30 31 32 33 34 35 36 37 38 39 | 0,39894 39892 39886 39876 39862 39844 39822 39797 39767 39733 39695 39654 39608 39559 39505 39448 39387 39322 39253 39181 39104 39024 38940 38853 38762 38667 38568 38466 38361 38251 38139 38023 37903 37780 37654 37524 37391 37255 37115 36973 | 0,40 41 42 43 44 45 46 47 48 49 0,50 51 52 53 54 55 56 57 58 59 0,60 61 62 63 64 65 66 67 68 69 0,70 71 72 73 74 75 76 77 78 79 | 0,36827 36678 36526 36371 36213 36053 35889 35723 35553 35381 35207 35029 34849 34667 34482 34494 34105 33912 33718 33521 33322 33121 32918 32713 32506 32297 32086 31874 31659 31443 31225 31006 30785 30563 30339 30114 29887 29659 29430 29200 | 0,80 81 82 83 84 85 86 87 88 89 0,90 91 92 93 94 95 96 97 98 99 1,00 01 02 03 04 05 06 07 08 09 1,10 11 12 13 14 15 16 17 18 19 | 0,28969 28737 28504 28269 28034 27798 27562 27324 27086 26848 26609 26369 26129 25888 25647 25647 25164 24923 24681 24439 0,24197 23955 23713 23471 23230 22988 22747 22506 22265 22025 21785 21546 21307 21069 20831 20594 20357 20121 19886 19652 | 1,20 21 22 23 24 25 26 27 28 29 1,30 31 32 33 34 35 36 37 38 39 1,40 41 42 43 44 45 46 47 48 49 1,50 51 52 53 54 55 56 57 58 59 | 0,19419 19186 18954 18724 18494 18265 18637 17810 17585 17360 17137 16915 16694 16474 16256 16038 15822 15608 15395 15183 14973 14764 14556 14350 14146 13943 13742 13542 13944 13147 0,12952 12758 12566 12376 12188 12001 11816 11632 11450 11270 | 1,60 61 62 63 64 65 66 67 68 69 1,70 71 72 73 74 75 76 77 78 79 1,80 81 82 83 84 85 86 87 88 89 1,90 91 92 93 94 95 96 97 98 99 | 0,11092 10915 10741 10567 10396 10226 10059 09893 09728 09566 09405 09246 09089 08933 08780 08628 08478 08329 08183 08038 07895 07754 07614 07477 07341 07206 07074 06943 06814 06687 06562 06438 06316 06195 06077 05959 05844 05730 05618 05508 | 2,00 01 02 03 04 05 06 07 08 09 2,10 11 12 13 14 2,15 16 17 18 19 2,20 21 22 23 24 25 26 27 28 29 2,30 31 32 33 34 35 36 37 38 39 | 0,05399 05292 05186 05082 04980 04879 04780 04682 04586 04491 04398 04307 04217 04128 04041 03955 03871 03788 03706 03626 03547 03470 03394 03319 03246 03174 03103 03034 02965 02898 02833 02768 02705 02643 02582 02522 02463 02406 02349 02294 |
Продовження таблиці 1 значень функції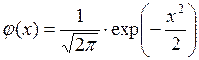
|
|
|
|
|
|
|
|
|
|
|
|
| 2,40 41 42 43 44 45 46 47 48 49 2,50 51 52 53 54 55 56 57 58 59 2,60 61 62 63 64 65 66 67 68 69 | 0,02239 02186 02134 02083 02033 01984 01936 01888 01842 01797 01750 01709 01667 01625 01585 01545 01506 01468 01431 01394 01358 01323 01289 01256 01223 01191 01160 01130 01100 01071 | 2,70 71 72 73 74 75 76 77 78 79 2,80 81 82 83 84 85 86 87 88 89 2,90 91 92 93 94 95 96 97 98 99 | 0,01042 01014 00987 00961 00935 00909 00885 00861 00837 00814 00792 00770 00748 00727 00707 00687 00668 00649 00631 00613 00595 00578 00562 00545 00530 00514 00499 00485 00470 00457 | 3,00 01 02 03 04 05 06 07 08 09 3,10 11 12 13 14 15 16 17 18 19 3,20 21 22 23 24 25 26 27 28 29 | 0,00443 00430 00417 00405 00393 00381 00370 00358 00348 00337 00327 00317 00307 00298 00288 00279 00271 00262 00254 00246 00238 00231 00224 00216 00210 00203 00196 00190 00184 00178 | 3,30 31 32 33 34 35 36 37 38 39 3,40 41 42 43 44 45 46 47 48 49 3,50 51 52 53 54 55 56 57 58 59 | 0,00172 00167 00161 00156 00151 00146 00141 00136 00132 00127 00123 00119 00115 00111 00107 00104 00100 06097 00094 00090 00087 00084 00081 00079 00076 00073 00071 00068 00066 00063 | 3,60 61 62 63 64 65 66 67 68 69 8,70 71 72 73 74 75 76 77 78 79 3,80 81 82 83 84 85 86 87 88 89 | 0,00061 00059 00057 00055 00053 00051 00049 00047 00046 00044 00042 00041 00039 00038 00037 00035 00034 00033 00031 00030 00029 00028 00027 00026 00025 00024 00023 00022 00021 00021 | 3,90 91 92 93 94 95 96 97 98 99 | 0,00020 00019 00018 00018 00017 00016 00016 00015 00014 00014 |
Таблиця 2. Значення функції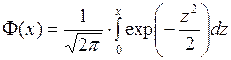 
|
| 
|
|
|
|
|
|
|
|
|
|
|
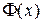
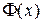
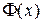
| 0,00 01 02 03 04 05 06 07 08 09 0,10 11 12 13 14 15 16 17 18 19 0,20 21 22 23 24 25 26 27 28 29 0,30 31 32 33 34 35 36 37 38 39 | 0,00000 00399 00798 01197 01595 01994 02392 02790 03188 03586 03983 04380 04776 05172 05567 05962 06356 06749 07142 07535 07926 08317 08706 09095 09483 09871 10257 10642 11026 11409 11791 12172 12552 12930 13307 13683 14058 14431 14803 15173 | 0,40 41 42 43 44 45 46 47 48 49 0,50 51 52 53 54 55 56 57 58 59 0,60 61 62 63 64 65 66 67 68 69 0,70 71 72 73 74 75 76 77 78 79 | 0,15542 15910 16276 16640 17003 17364 17724 18082 18439 18793 19146 19497 19847 20194 20540 20884 21226 21566 21904 22240 22575 22907 23237 23565 23891 24215 24537 24857 25175 25490 25804 26115 26424 26730 27035 27337 27637 27935 28230 28524 | 0,80 81 82 83 84 85 86 87 88 89 0,90 91 92 93 94 95 96 97 98 99 1.00 01 02 03 04 05 06 07 08 09 1,10 11 12 13 14 15 16 17 18 19 | 0,28814 29103 29389 29673 29955 30234 30511 30785 31057 31327 31594 31859 32121 32381 32639 32894 33147 33398 33646 33891 34134 34375 34614 34850 35083 35314 35543 35769 35993 36214 36433 36650 36864 37076 37286 37493 37698 37900 38100 38298 | 1,20 21 22 23 24 25 26 27 28 29 1,30 31 32 33 34 35 36 37 38 39 1,40 41 42 43 44 45 46 47 48 49 1,50 51 52 53 54 55 56 57 58 59 | 0,38493 38686 38877 39065 39251 39435 39617 39796 39973 40147 40320 40490 40658 40824 40988 41149 41309 41466 41621 41774 41924 42073 42220 42364 42507 42647 42786 42922 43056 43189 43319 43448 43574 43699 43822 43943 44062 44179 44295 44408 | 1,60 61 62 63 64 65 66 67 68 69 1,70 71 72 73 74 75 76 77 78 79 1,80 81 82 83 84 85 86 87 88 89 1,90 91 92 93 94 95 96 97 98 99 | 0,44520 44630 44738 44845 44950 45053 45154 45254 45352 45449 45543 45637 45728 45818 45907 45994 46080 46164 46246 46327 46407 46485 46562 46638 46712 46784 46856 46926 46995 47062 47128 47193 47257 47320 47381 47441 47500 47558 47615 47670 | 2,00 01 02 03 04 05 06 07 08 09 2,10 11 12 13 14 15 16 17 18 19 2,20 21 22 23 24 25 26 27 28 29 2,30 31 32 33 34 35 36 37 38 39 | 47725 47778 47831 47882 47932 47932 48030 48077 48124 48169 48214 48257 48300 48311 48382 48422 48461 48500 48537 48574 48610 48645 48679 48713 48745 48778 48809 48840 48870 48899 48928 48956 48983 49010 49036 49061 49086 49111 49134 49158 |
Продовження таблиці 2 значень функції 
|
|
|
|
|
|
|
|
|
| 2,40 41 42 43 44 45 46 47 48 49 2,50 51 52 53 54 55 56 57 58 59 | 0,49180 49202 49224 49245 49266 49286 49305 49124 49343 49361 0,49379 49396 49413 49430 49446 49461 49477 49492 49506 49520 | 2,60 61 62 63 64 65 66 67 68 69 2,70 71 72 73 74 75 76 77 78 79 | 0,49534 49547 49560 49573 49585 49598 49609 49621 49632 49643 0,49653 49664 49674 49683 49693 49702 49711 49720 49728 49736 | 2,80 81 82 83 84 85 86 87 88 89 2,90 91 92 93 94 95 96 97 98 99 | 0,49744 49752 49760 49767 49774 49781 49788 49795 49801 49807 0,49813 49819 49825 49831 49836 49841 49846 49851 49856 49861 | 3,0 1 2 3 4 5 6 7 8 9 4,0 4,5 5,0 | 0,40865 49903 49931 49952 49966 49977 49984 49989 49993 49995 499968 499997 499999 |
Таблиця 3. Критичні точки розподілу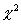 
Таблиця 4. Значення функції Колмогорова.
| 
| 
|
| 
|
|
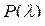
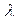
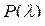
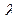
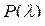
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0,33 0,34 0,35 0,35 0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 0,80 | – – 0,0001 0,0002 0,0003 0,0005 0,0008 0,0013 0,0019 0,0028 0,0040 0,0055 0,0074 0,0097 0,0186 0,0160 0,0200 0,0247 0,0300 0,0361 0,0428 0,0503 0,0585 0,0674 0,0772 0,0876 0,0987 0,1104 0,1228 0,1357 0,1492 0,1632 0,1778 0,1927 0,2080 0,2236 0,2396 0,2558 0,2722 0,2888 0,3055 0,3223 0,3301 0,3560 0,3728 0,3896 0,4064 0,4230 0,4395 0,4559 | 0,81 0,82 0,83 0,84 0,85 0,85 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 1,30 | 0,4720 0,4880 0,5038 0,5194 0,5347 0,5497 0,5645 0,5791 0,5933 0,6073 0,6209 0,6343 0,6473 0,6601 0,6725 0,6846 0,6994 0,7079 0,7191 0,7300 0,7406 0,7508 0,7608 0,7704 0,7798 0,7889 0,7976 0,8061 0,8143 0,8222 0,8300 0,8374 0,8445 0,8514 0,8580 0,8644 0,8706 0,8765 0,8829 0,8878 0,8930 0,8981 0,9030 0,9076 0,9121 0,9164 0,9206 0,9245 0,9283 0,9319 | 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 1,59 1,60 1,61 1,63 1,65 1,80 1,85 1,90 1,95 2,00 2,05 2,10 2,15 2,20 2,25 2,30 2,35 2,40 2,50 3,00 | 0,9354 0,9387 0,9418 0,9448 0,9478 0,9505 0,9531 0,9557 0,9580 0,9603 0,9625 0,9646 0,9665 0,9684 0,9702 0,9718 0,9734 0,9750 0,9764 0,9778 0,9791 0,9803 0,9815 0,9826 0,9836 0,9846 0,9855 0,9864 0,9873 0,9880 0,9914 0,9938 0,9956 0,9969 0,9979 0,9985 0,9990 0,9993 0,9996 0,9997 0,9998 0,9998 0,9999 0,99995 0,99997 0,99998 0,99999 0,99999 |
Таблиця 5 . Значення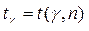 
| n | g | n | g | ||||
| 0,95 | 0,99 | 0,999 | 0,95 | 0,99 | 0,999 | ||
| 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10 | 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88 | 8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 | 20 25 30 35 40 45 50 60 70 80 90 100 120 ¥ | 2,093 2,064 2,045 2,032 2,023 2,016 2,009 2,001 1,996 1,991 1,987 1,984 1,980 1,960 | 2,861 2,797 2,756 2,720 2,708 2,692 2,679 2,662 2,649 2,640 2,633 2,627 2,617 2,576 | 3,883 3,745 3,659 3,600 3,558 3,527 3,502 3,464 3,439 3,418 3,403 3,392 3,374 3,291 |
Таблиця 6. Значення критерію Фішера (F-критерію) для рівню значимості p = 0,05. f1 – число ступіней свободи більшої дисперсії, f2 - число ступіней свободи меншої дисперсії
| f 1 | |||||||||||
| f 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 |
| 1 | 161.45 | 199.50 | 215.71 | 224.58 | 230.16 | 233.99 | 236.77 | 238.88 | 240.54 | 241.88 | 245.95 |
| 2 | 18.51 | 19.00 | 19.16 | 19.25 | 19.30 | 19.33 | 19.35 | 19.37 | 19.38 | 19.40 | 19.43 |
| 3 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 | 8.81 | 8.79 | 8.70 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.86 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.77 | 4.74 | 4.62 |
| 6 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 3.94 |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.64 | 3.51 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.35 | 3.22 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.14 | 3.01 |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.98 | 2.85 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.85 | 2.72 |
| 12 | 4.75 | 3.89 | 3.49 | 3.26 | 3.11 | 3.00 | 2.91 | 2.85 | 2.80 | 2.75 | 2.62 |
| 13 | 4.67 | 3.81 | 3.41 | 3.18 | 3.03 | 2.92 | 2.83 | 2.77 | 2.71 | 2.67 | 2.53 |
| 14 | 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.76 | 2.70 | 2.65 | 2.60 | 2.46 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.71 | 2.64 | 2.59 | 2.54 | 2.40 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | 2.35 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.61 | 2.55 | 2.49 | 2.45 | 2.31 |
| 18 | 4.41 | 3.55 | 3.16 | 2.93 | 2.77 | 2.66 | 2.58 | 2.51 | 2.46 | 2.41 | 2.27 |
| 19 | 4.38 | 3.52 | 3.13 | 2.90 | 2.74 | 2.63 | 2.54 | 2.48 | 2.42 | 2.38 | 2.23 |
| 2 0 | 4.35 | 3.49 | 3.10 | 2.87 | 2.71 | 2.60 | 2.51 | 2.45 | 2.39 | 2.35 | 2.20 |
Методичні вказівки
Методичні вказівки до виконання індивідуальних робіт з дисципліни “Теорія ймовірностей та математична статистика” для студентів спеціальності “Соціологія”. Частина 2.
Укладачі:
Дата: 2019-02-02, просмотров: 513.
