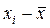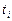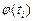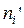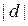Правила оформлення контрольної роботи

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ЗМІСТ

ВСТУП.. 4

Правила оформлення контрольної роботи.. 4

1. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ.. 5

1.1. Основні поняття. 5

1.2. Поняття оцінки характеристик генеральної сукупності. 8

1.3. Числові характеристики статистичного розподілу. 9

1.4. Метод добутків обчислення вибіркових середнього. 17

2. ПЕРЕВІРКА СТАТИСТИЧНИХ ГІПОТЕЗ. 18

2.1. Основні поняття. 18

2.2. Критерій для перевірки гіпотези про імовірність події 19

2.3. Критерій для перевірки гіпотези про математичне сподівання. 21

2.4. Критерій для перевірки гіпотези про порівняння двох дисперсій. 22

2.5. Критерій Пирсона для перевірки гіпотези про вид закону розподілу випадкової величини. 23

2.6. Критерій Колмогорова. 30

3. КОРЕЛЯЦІЙНИЙ ТА РЕГРЕСІЙНИЙ АНАЛІЗ. 34

4. КОНТРОЛЬНА РОБОТА.. 38

5. ЛІТЕРАТУРА.. 50

6. ДОДАТОКИ.. 51

ВСТУП

У зв'язку зі специфікою навчального процесу студентів соціологічних спеціальностей актуальною є методична розробка за основними темами курсу “Теорія ймовірностей та математична статистика”, яка призначена для теоретичного і практичного вивчення. Знання, отримані при вивченні цього курсу необхідні студентам для освоєння спеціальних дисциплін.

Для закріплення вивченого теоретичного матеріалу, а також для набуття навичок і вмінь практичного використання отриманих знань, студентам пропонується виконати індивідуальну самостійну роботу за курсом.

Вибір варіанта здійснюється таким чином: беремо останню цифру номера з журналу і це Ваш варіант.

Робота, виконана не за своїм варіантом, не приймається.

Правила оформлення контрольної роботи

1) Контрольну роботу варто виконувати в окремому зошиті, залишаючи поля для зауважень рецензента.

2) У заголовку роботи потрібно зазначити таке: назву дисципліни, факультет, курс, група, прізвище студента, ім'я та по батькові, номер індивідуального плану. Заголовок роботи треба помістити на обкладинці зошита.

3) Перед розв’язанням кожної задачі потрібно записати цілком її умову.

4) Розв’язання задач варто викладати докладно, пояснюючи дії.

5) Наприкінці виконаної роботи необхідно перерахувати використану для виконання літературу.

Захист індивідуальної роботи проводиться у формі співбесіди за темою роботи.

ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ

Основні поняття

Нехай потрібно досліджувати будь-яку ознаку, яка притаманна великій групі однотипних виробів (наприклад: розмір деталей даного типу, вагу виробу тощо)

Сукупність значень ознаки усіх N виробів даного типу називається генеральною сукупністю.

Вибірковою сукупністю, або просто вибіркою, називають сукупність випадково відібраних об'єктів. Ці вибірки реально спостерігаються в експерименті. Кількість цих даних називається об'ємом вибірки. Теоретично вибірка є сукупність незалежних однаково розподілених випадкових величин, розподіл яких співпадає з розподілом генеральної сукупності.

Вибірковий метод полягає в тому, що з генеральної сукупності береться вибірка обсягу п (причому п << N) і визначаються характеристики вибірки, що приймаються в якості наближених значень відповідних характеристик генеральної сукупності.

Вибірки бувають повторні (з поверненням відібраного елемента до генеральної сукупності) та безповторпі (без повернення).

Вибірки розрізняються за способом відбору: простий випадковий відбір (елементи відбирають по одному з генеральної сукупності), типовий відбір (елементи відбирають з деякої частини генеральної сукупності), механічний відбір (елементи відбирають по одному з кожної частини генеральної сукупності), серійний відбір (елементи відбирають серіями).

Різні елементи вибірки називаються варіантами і позначаються 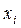. Число, що показує, скільки разів зустрічається варіанта в даній вибірці, називається частотою і позначається 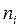. Сума частот дорівнює об'єму вибірки (загальному числу спостережень 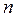). Відношення частоти до об'єму вибірки називається відносною частотою, тобто 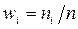. Сума відносних частот дорівнює одиниці.

Для проведення статистичного аналізу необхідно вибірки, що розглядаються представити у зручному і сприйнятливому вигляді. Для цього складають статистичний розподіл вибірки.

Припустимо, що вивчається деяка випадкова величина Х, закон розподілу якої невідомий. Над випадковою величиною Х проводиться ряд незалежних спостережень (вимірів). Результати вимірів подають у вигляді таблиці, що складається з двох рядків, у першому із яких указуються номера вимірів i, а у другому – результати вимірів х_i :

і	1	2	…	п
x_i	x₁	x₂	…	x_n

Таблицю, що вміщує номера і результати вимірів, називають рядом варіант або статистичним рядом.

Варіаційним рядом вибірки називають засіб її запису, при якому елементи х_i (варіанти) розташовані за розміром, тобто записуються в зростаючому порядку. Різниця між максимальним і мінімальним елементами вибірки називається розмахом вибірки. Рівні між собою члени нумеруються в довільному порядку. Ці дії називаються рангуванням статистичних даних.

Нехай у вибірці обсягу п елемент x_i зустрічається n_i разів. Число n_i називається частотою елемента x_i. При цьому 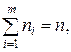де т – число різноманітних варіант n_i._.

Відношення 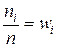називаються відносними частотами і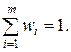

Статистичним розподілом (розподілом частот) вибірки називають перелік варіант і відповідних їм частот.

Його можна також записати у вигляді послідовності інтервалів і відповідних їм частот. У якості частоти, що відповідає інтервалу, приймають суму частот, що потрапили в цей інтервал, причому якщо при угрупованні значень що спостерігаються, маємо значення, що у точності лежить на межі двох інтервалів, то варто додати до числа n_i однієї і іншої груп по 1/2 частоти, що відповідає даному значенню.

З метою наочності будують різноманітні графіки статистичного розподілу і, зокрема, полігон і гістограму.

Полігоном частот називається ломана, відрізки якої з'єднують точки з координатами (x₁, n₁),...,( x_m, n_m).

Полігоном відносних частот називають ломану, що з'єднує точки з координатами (x₁, w₁),...,( x_m, w_m).

У випадку неперервноі ознаки (наприклад, дальність польоту снаряда) або при великому числі значень ознаки доцільно будувати гістограму частот, для чого інтервал, у якому укладені всі значення ознаки, розбивають на декілька часткових інтервалів довжиною h і знаходять для кожного i-го часткового інтервалу частоту n_i, що дорівнює сумі частот варіант, що потрапили в i-й інтервал.

Гістограмою частот називають ступінчасту фігуру, що складається з прямокутників, основами яких є часткові інтервали довжиною h, а висоти дорівнюють відношенню 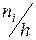(щільність частоти). Площа i-го часткового прямокутника дорівнює 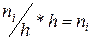- сумі частот варіант i-го інтервалу; отже, площа гістограми частот дорівнює сумі всіх частот, тобто обсягу вибірки.

Гістограмою відносних частот називають ступінчасту фігуру, що складається з прямокутників, основами яких є часткові інтервали довжиною h 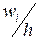а висоти дорівнюють відношенню 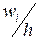(щільність відносної частоти). Площа гістограми відносних частот дорівнює сумі площ усіх прямокутників, тобто

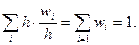
Емпіричною функцією розподілу називають функцію , яка визначає для кожного значення х відносну частоту події Х<х, тобто 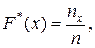де 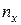– число варіант, менших х, п - обсяг вибірки.

З визначення випливають такої її властивості:

1) значення емпіричної функції належать відрізку [0;1];

2) - функція , що не убуває;

3) якщо x₁ – найменша варіанта, то 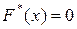при ;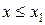

якщо х_k - найбільша варіанта, то 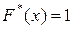при х > х_k;

Емпіричну функцію розподілу 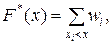можна також визначити як суму відносних частот варіант, менших х.

ПРИКЛАД 1 . При обстеженні студентів першого курсу за віком були зафіксовані наступні дані (табл. 1). Побудувати полігон розподілу.

Таблиця 1.

Розподіл студентів першого курсу за віком

Вік студентів (варіанты x_i)	Число студенів з даним віком (частоти n_i)	Частости (f_i)
Вік студентів (варіанты x_i)	Число студенів з даним віком (частоти n_i)	відносні	в %
17 18 19 20 21 22 23	2 15 14 6 6 5 2	0,04 0,30 0,28 0,12 0,12 0,10 0,04	4 30 28 12 12 10 4
Разом	50	1,0	100

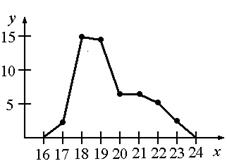
Рис.1. Полігон розподілу студентів за віком

У прямокутній системі координат на горизонтальній осі відкладаємо значення ознаки (вік студентів), а на вертикальній осі – частоти (число студентів з даним віком). Отримані крапки з'єднаємо відрізками прямої. Для того щоб фігура була замкнутої, уведемо додатково нові значення ознаки (16 років, 24 роки); відповідні їм частоти, природно, дорівнюють нулю. У результаті одержимо полігон розподілу студентів за віком (мал. 1).

ПРИКЛАД 2. Побудуємо гістограму розподілу душ за розміром прирізки в Бєльському повіті Смоленської губернії за даними табл.2. (За браком додаткових даних при побудові графіка скористаємося припущенням, що величина останнього відкритого інтервалу дорівнює величині попереднього).

Таблиця 2 Розподіл душ за розміром прирізки в Бєльському повіті Смоленської губернії.

Размір прирізки x_i	Кількість душ, до ділянок яких зроблені прирізки n_i, %
До 10 11-20 21-30 31-40 41-50 Більш 50	24,5 26,7 19,3 9,7 5,8 14,0
Разом	100,0

Рис.2. Полігон частот

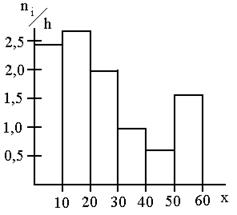
Як уже відзначалося, для інтервального ряду також можна побудувати полігон розподілу. Для цього за значення ознаки приймають середини інтервалів і для отриманого дискретного ряду звичайним способом будують полігон. Результати такої побудови зображені на рис 2.

Основні поняття

Статистичною гіпотезою називається будь-яке припущення щодо виду або параметрів невідомого розподілу.

Розрізняють прості й складні статистичні гіпотези. Простою називають гіпотезу, яка містить тільки одне припущення. Наприклад, якщо l - параметр показникового розподілу, то гіпотеза 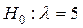– проста.

Складною називають гіпотезу, що складається з скінченого або нескінченного числа простих гіпотез. Наприклад, гіпотеза 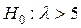складна та складається з незліченної множини простих гіпотез 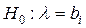, де 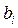- будь-яке число більше 5.

Гіпотезу, що перевіряють, називають нульовою (або основною) і позначають 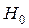. Альтернативною ( або конкуруючою) називають гіпотезу 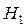, що є логічним запереченням 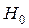і яку ми приймаємо, якщо відкидаємо основну гіпотезу.

Приклад. Нехай Н₀ полягає в тому, що математичне сподівання генеральної сукупності а = 3. Тоді ймовірні варіанти Н₁: а) а≠3; б) а>3; в) а<3.

При перевірці гіпотез можуть виникнути помилки двох видів. Помилка першого роду полягає в тому, що буде відкинута гіпотеза 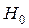, коли вона вірна.

Ймовірність помилки першого роду позначають a і називають рівнем значущості критерію.

Помилка другого роду полягає в тому, що буде прийнята гіпотеза 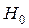, коли вона невірна. Ймовірність цієї помилки позначають b .

Ймовірність 1-b не припуститися помилки другого роду, тобто відкинути гіпотезу 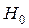, коли вона невірна, називається потужністю критерію. Чим більше потужність критерію, тим менше ймовірність помилки другого роду.

Яка з помилок є на практиці більш небезпечною, залежить від конкретної задачі. Наприклад, якщо перевіряється правильність вибору методу лікування хворого, то помилка першого роду означає відмовлення від правильної методики, що може сповільнити лікування, а помилка другого роду (застосування неправильної методики) чревата погіршенням стану хворого і є більш небезпечної.

Для перевірки нульової гіпотези використовують спеціально підібрану випадкову величину, яку називають статистичним критерієм.

Спостережуваним значенням критерію називається значення критерію, що обчислюється за вибіркою.

Після вибору статистичного критерію множину всіх його можливих значень розбивають на дві області, які не перетинаються. Це область відхилення нульової гіпотези та область прийняття цієї гіпотези. Критичною областю називається сукупність значень критерію, при яких нульову гіпотезу відкидають. Областю прийняття гіпотези називається сукупність значень критерію, при яких нульову гіпотезу приймають.

Основний принцип перевірки статистичних гіпотез: якщо спостере жуване значення критерію належить критичній області, гіпотезу відкидають; якщо спостережуване значення належить області прийняття гіпотези - гіпотезу приймають.

Отже, процес перевірки гіпотези складається з наступних етапів:

1. Вибирається статистичний критерій ДО.

2. Обчислюється його значення, що спостерігається, К_набл по наявній вибірці.

3. Оскільки закон розподілу ДО відомий, визначається (за відомим рівнем значимості α) критичне значення k_кр, що розділяє критичну область й область прийняття гіпотези (наприклад, якщо р(ДО > k_кр) = α, то праворуч від k_кр розташовується критична область, а ліворуч – область прийняття гіпотези).

4. Якщо обчислене значення К_спост попадає в область прийняття гіпотези, то нульова гіпотеза приймається, якщо в критичну область – нульова гіпотеза відкидається.

Розрізняють різні види критичних областей:

· правобічну критичну область, обумовлену нерівністю K > k_кр ( k_кр > 0);

· лівосторонню критичну область, обумовлену нерівністю K < k_кр ( k_кр < 0);

· двосторонню критичну область, обумовлену нерівностями K < k₁, K > k₂(k₂> k₁).

Потужністю критерію називають імовірність потрапляння критерію в критичну область за умови, що вірна конкуруюча гіпотеза. Після вибору рівня значимості варто будувати критичну область так, щоб потужність критерію була максимальною.

Критерій Колмогорова

Критерій призначений для зіставлення двох розподілів: а) емпіричного з теоретичним; б) одного емпіричного розподілу з іншим емпіричним розподілом.

Критерій дозволяє знайти точку, у якій сума накопичених розбіжностей між двома розподілами є найбільшої й оцінити вірогідність цієї розбіжності. Найчастіше застосуються для перевірки простої гіпотези Н₀ про те, що незалежні однаково розподілені випадкові величини Х₁, Х₂, …, Х_п мають задану безупинну функцію розподілу F(x).

Гіпотези:

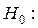розходження між двома розподілами недостовірні;

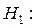розходження між двома розподілами достовірні (судячи з точки максимально накопиченої розбіжності між ними).

Обмеження критерію. Критерій вимагає досить великої вибірки при зіставленні двох емпіричних розподілів (більше чи дорівнює 50). При зіставленні емпіричного розподілу з теоретичним допускається n більше чи дорівнюючі 5.

Алгоритм розрахунку абсолютної величини різниці d між емпіричним і рівномірним розподілами.

1. Занести в таблицю найменування розрядів і відповідні їм емпіричні частоти (перший стовпець).

2. Підрахувати відносні емпіричні частоти для кожного розряду за формулою: 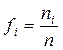, де: 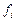– емпірична частота по даному розряду, n – загальна кількість спостережень. Занести результати в другий стовпець.

3. Підрахувати накопичені емпіричні частоти за формулою:

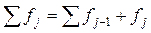де 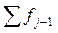– частота, накопичена на попередніх розрядах;

j – порядковий номер розряду;

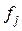– емпірична частота даного j-го розряду.

Занести результати в третій стовпець таблиці.

4. Підрахувати накопичені теоретичні частоти для кожного розряду за формулою:

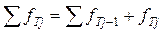де: 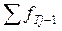– теоретична частота, накопичена на попередніх розрядах;

j – порядковий номер розряду;

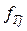– теоретична частота даного розряду. Занести результати в четвертий стовпець таблиці.

5. Обчислити різниці між емпіричними й теоретичними накопиченими частотами за кожнім розрядом.

6. Записати в п'ятий стовпець абсолютні величини отриманих різностей (без обліку їхнього знака). Позначити їх як d.

7. Визначити по п'ятому стовпці найбільшу величину різниці .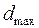

8. Обчислити величину 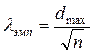. Виходячи з таблиць, визначити при заданому рівні надійності 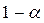зі співвідношення 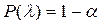табличне значення критерію 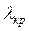. Якщо отримане емпіричне число 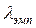перевищують критичне 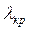– розходження достовірні.

ПРИКЛАД 9. Визначити параметри емпіричного й теоретичного розподілів та за допомогою критерію Колмогорова оцінити близькість емпіричного розподілу до нормального при рівні значимості .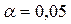

Вихідні дані дано втаблиці.

Таблиця 12

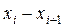
	306- 311	311- 316	316- 321	321- 326	326- 331	331- 336	336- 341	341- 346	346- 351	351- 356
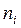
	19	34	38	33	38	17	11	6	2	2

За допомогою методу умовних моментів визначаємо середню величину 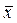і середньоквадратичне відхилення 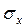. Розрахунки представлені в наступній таблиці

Таблиця 13

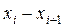
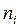
		Середина інтервалу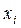
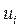
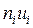
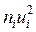
306-311 311-316 316-321 321-326 326-331 331-336 336-341 341-346 346-351 351-356	19 34 38 33 38 17 11 6 2 2	308,5 313,5 318,5 323,5 328,5 333,5 338,5 343,5 348,5 353,5	-4 -3 -2 -1 0 1 2 3 4 5	-76 -102 -76 -33 0 17 22 18 8 10	304 306 152 33 0 17 44 54 32 50
Разом	200			-212	992

Умовні моменти

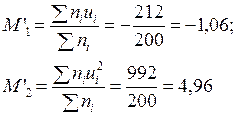
Вибіркові середня і середньоквадратичне відхилення

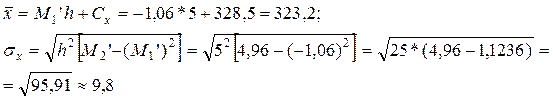
Розрахуємо теоретичні частоти (див. наступну таблицю). Для цього визначаємо нормовані відхилення 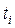(графа 4), по додатку встановлюємо значення функції 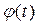(графа 5), розраховуємо теоретичні частоти по формулі

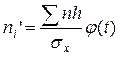
За даними розглянутого приклада

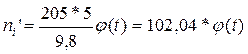
Таблица 1 4

Уточ-нена

теор. частота

Накопичена

частота

Фак-тична

Теоре-тична

296-301 301-306 306-311 311-316 316-321 321-326 326-331 331-336 336-341 341-346 346-351 351-356

- - 19 34 38 33 38 17 11 6 2 2

-24,7 -19,7 -14,7 -9,7 -4,7 -0,3 5,3 10,3 15,3 20,3 25,3 30,3

-2,52 -2,01 -1,50 -0,99 -0,48 -0,03 -,54 1,05 1,56 2,07 2,58 3,10

0,0167 0,0529 0,1296 0,2444 0,3565 0,3988 0,3448 0,2299 0,1182 0,0468 0,0143 0,0033

- - 13 25 36 41 35 24 12 5 1 -

2 6 13 25 36 41 35 24 12 5 1 -

- - 19 53 91 124 162 179 190 196 198 200

2 8 21 46 82 123 158 182 184 199 200 200

2 8 2 7 9 1 4 3 4 3 2 0

З огляду на те, що теоретичні частоти можуть бути тільки цілими числами, округляємо їх і знаходимо суму, що дорівнює 192. Таким чином, має місце розбіжність сум теоретичних частот (192) і фактичних (200). У даному випадку така розбіжність може бути пояснено відмінністю крайніх теоретичних частот від нуля. Тому теоретичну криву треба продовжити. У нашому прикладі нормальна крива може бути продовжена убік від'ємних відхилень від середньої. Робимо розрахунок теоретичних частот для перших двох інтервалів і одержуємо значення частот, що дорівнюють 2 і 6. Далі визначаємо накопичені фактичні й теоретичні частоти. Розраховуємо різницю між ними й встановлюємо максимальну розбіжність 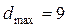(п'ятий інтервал). Обчислюємо величину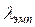

За даними таблиці додатка знаходимо при рівні значимості 0,05

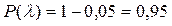табличне значення критерію 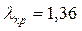. Так як (0,636<1,36), то гіпотеза про нормальний розподіл досліджуваної ознаки приймається.

КОНТРОЛЬНА РОБОТА

ЗАДАЧА 1. Задано вибірку, що отримана для дискретної випадкової величини. Обробивши її, побудувати:

1) варіаційний ряд;

2) статистичний розподіл вибірок у частотах і відносних частотах;

3) полігон частот;

4) знайти чисельні характеристики вибірки:

· вибіркову середню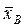

· статистичні моду Мо і медіану Ме

· статистичні дисперсію 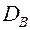і середньоквадратичне відхилення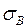

№1

12 6 8 10 4 9 8 12 9 12 8 7 14 7 16 5 11 7 4 5 8 5 8 4 7 9 9 6 9 5

№2

2 4 8 5 9 3 5 9 4 10 15 9 5 10 5 7 7 12 8 6 13 9 5 11 9 13 11 12 8 4

№3

5 10 7 7 8 10 13 7 10 5 7 10 10 11 9 16 12 10 7 5 13 7 12 6 13 12 13 12 8 14

№4

13 19 8 12 15 15 13 12 17 13 17 15 19 14 13 15 13 18 13 8 8 9 14 16 9 14 19 15 12 11

№5

8 10 8 8 7 5 3 6 9 6 9 8 8 4 15 5 7 4 10 10 5 3 6 11 7 6 9 8 11 11

№6

3 0 1 1 2 2 2 0 1 1 1 1 0 4 3 1 1 3 3 1 2 1 1 3 4 3 3 2 2 2

№7

2 3 1 4 3 1 1 2 1 2 3 4 1 4 3 5 3 4 1 2 5 4 2 4 4 3 3 4 5 4

№8

2 2 1 1 3 1 3 2 0 2 3 3 2 1 1 2 2 3 2 2 2 2 2 3 2 3 2 2 3 3

№9

3 2 3 4 2 2 2 3 2 1 3 1 2 2 2 1 2 1 4 2 3 3 3 1 1 2 4 2 3 2

№10

3 2 1 3 1 2 1 1 4 2 1 3 3 4 2 2 2 4 3 1 1 4 3 3 1 0 3 2 3 4

ЗАДАЧА 2. Задано вибірку, отримана для безупинної випадкової величини, Обробивши її, побудувати:

1) варіаційний ряд.

2) виконати інтервальну угруповання даних.

3) побудувати гістограму відносних частот.

4) знайти чисельні характеристики вибірки:

· вибіркову середню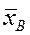

· статистичні моду Мо і медіану Ме

· статистичні дисперсію 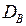і середньоквадратичне відхилення .

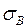№1

1,65 7,86 6,96 4,95 1,88 0,23 0,39 5,16 0,71 5,56 0,73 23,92 3,01 6,79 3,49 1,11 8,72 24,08 0,62 2,06 7,93 4,96 6,67 2,57 0,98 12,32 1,65 3,03 7,32 0,42

№2

7,43 6,44 17,77 7,74 19,52 5,97 4,75 31,92 4,27 39,68 1,37 17,13 3,31 0,55 1,01 6,83 1,31 6,45 0,69 3,56 9,15 9,89 2,10 9,46 1,67 0,08 0,44 6,25 0,90 9,30

№3

0,16 0,77 6,57 0,61 9,10 26,43 6,73 0,86 8,44 0,91 2,56 3,41 13,74 3,99 1,77 18,34 6,16 1,01 11,63 6,86 19,76 12,44 14,18 4,78 0,53 0,42 5,83 1,85 1,92 3,17

№4

12,93 26,27 3,21 11,19 0,87 4,66 11,37 14,37 18,65 10,07 50,78 19,96 12,64 3,04 0,73 16,04 2,81 23,90 1,74 27,30 20,94 28,65 22,97 6,65 35,39 5,19 24,64 0,31 2,60 9,54

№5

12,88 8,71 9,64 12,31 10,26 12,48 17,49 4,42 4,65 14,71 10,15 11,69 7,42 20,38 13,61 8,60 9,68 10,92 15,35 7,08 6,05 21,58 5,39 9,87 14,28 6,23 8,94 19,51 3,61 10,18

№6

0,40 1,75 0,47 1,57 2,07 0,73 3,86 5,27 0,43 2,25 2,05 1,50 1,23 3,67 1,34 1,54 2,49 1,15 0,67 1,31 1,95 1,77 0,50 0,49 0,40 1,94 0,91 8,60 1,91 3,59

№7

1,50 0,93 1,40 0,41 0,54 0,47 5,19 1,04 0,31 1,56 0,52 0,61 2,04 1,15 1,20 1,43 0,71 1,32 0,90 0,72 0,85 0,56 1,98 0,50 0,71 0,32 0,38 0,36 0,56 2,17 1,44

№8

-3,29 0,18 4,02 11,38 5,74 9,11 11,17 0,44 9,79 -0,27 -5,55 2,37 6,66 -2,12 3,99 0,67 -1,74 3,69 1,65 3,61 7,72 5,13 5,87 8,62 1,39 4,00 1,67 3,37 7,29 0,62

№9

3,63 9,34 15,16 -6,46 -13,19 -7,92 7,06 12,34 14,46 -15,45 11,51 1,62 15,04 -7,90 -6,04 8,35 11,70 4,69 -3,47 0,44 -4,24 3,57 14,35 7,89 5,56 14,43 5,56 6,76 -4,17 3,01

№10

-5,52 13,13 -14,81 21,07 13,98 8,87 -0,63 9,14 7,35 -2,35 5,98 16,67 13,92 21,64 0,18 -0,62 8,72 13,94 2,72 13,74 -0,96 18,34 7,88 0,13 -8,66 16,50 27,44 -6,34 -0,34 18,58

ЗАДАЧА 3. Задано вибірку, Необхідно:

1) побудувати статистичну функцію розподілу 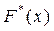. Записати її аналітичне вираження. Побудувати графік.

2) виконати інтервальну оцінку параметрів розподілу:

· Математичного сподівання ,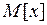

· Середньоквадратичного відхилення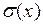

(Довірчу імовірність 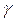прийняти рівної 0,95)

№1

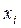
	2	5	7	9	11	13	17
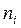
	11	15	9	13	25	17	10

№2

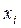
	12	14	18	21	25	27	31
	10	15	22	31	24	14	9

№3

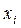
	1	3	7	9	11	14	21
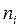
	36	32	21	19	15	22	34

№4

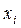
	3	5	6	8	11	12	15
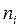
	22	31	24	23	28	32	19

№5

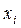
	2	5	7	9	13	16	18
	18	14	13	19	22	34	45

№6

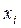
	1	4	5	8	10	13	15
	34	43	25	29	34	28	30

№7

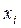
	4	5	7	8	9	11	13
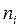
	21	23	24	19	17	22	25

№8

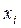
	4	6	8	12	14	15	17
	11	12	9	16	19	21	15

№9

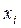
	1	3	5	9	11	14	17
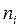
	24	25	33	21	17	15	22

№10

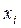
	2	3	4	6	7	9	10
	34	31	27	24	22	17	13

ЗАДАЧА 4. Задано вибірку, отримана для безупинної випадкової величини X. Обробивши її, записати гіпотезу про вид закону розподілу. Перевірити гіпотезу, використовуючи критерій Пірсона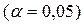

№1.

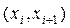
	(2;4)	(4;6)	(6;8)	(8;10)	(10;12)	(12;14)	(14;16)
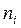
	49	35	24	17	9	5	1

№2.

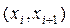
	(0;3)	(3;6)	(6;9)	(9;12)	(12;15)	(15;18)	(18;21)
	13	8	12	10	9	11	10

№3.

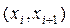
	(0;5)	(5;10)	(10;15)	(15;20)	(20;25)	(25;30)	(30;35)
	2	16	34	35	31	13	1

№4.

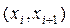
	(1;3)	(3;5)	(5;7)	(7;9)	(9;11)	(11;13)	(13;16)
	65	50	37	21	12	4	2

№5.

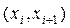
	(0;4)	(4;8)	(8;12)	(12;16)	(16;20)	(20;24)	(24;28)
	37	43	34	41	45	39	42

№6.

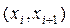
	(-1;1)	(1;3)	(3;5)	(5;7)	(7;9)	(9;11)	(11;13)
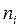
	4	12	24	37	19	9	2

№7.

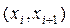
	(-6;-3)	(-3;0)	(0;3)	(3;6)	(6;9)	(9;12)	(12;15)
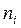
	44	25	18	11	4	2	1

№8.

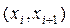
	(-5;-1)	(-1;3)	(3;7)	(7;11)	(11;15)	(15;19)	(19;23)
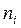
	4	16	28	35	31	19	6

№9.

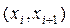
	(2;4)	(4;6)	(6;8)	(8;10)	(10;12)	(12;14)	(14;16)
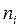
	27	31	29	33	30	24	22

№10.

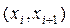
	(0;3)	(3;6)	(6;9)	(9;12)	(12;15)	(15;18)	(18;21)
	3	8	22	43	29	11	5

ЗАДАЧА 5. Задано вибірку, що отримана для дискретної випадкової величини X. Перевірити гіпотезу про вид закону розподілу, використовуючи критерій Пірсона (a = 0,05).

№1. Розподіл Пуассона.

x_i	0	1	2	3	4	5
n_i	269	175	41	9	4	2

№2. Біноміальний розподіл.

x_i	0	1	2	3	4	5
n_i	2	4	15	51	17	8

№3. Розподіл Пуассона.

x_i	0	1	2	3	4	5
n_i	301	132	54	10	2	1

№4. Біноміальний розподіл.

x_i	0	1	2	3	4	5
n_i	3	6	18	47	19	7

№5. Розподіл Пуассона.

x_i	0	1	2	3	4	5
n_i	285	144	39	12	4	2

№6. Біноміальний розподіл.

x_i	0	1	2	3	4	5
n_i	6	11	25	67	21	14

№7. Розподіл Пуассона.

x_i	0	1	2	3	4	5
n_i	315	196	58	17	0	3

№8. Біноміальний розподіл.

x_i	0	1	2	3	4	5
n_i	3	7	22	65	19	13

№9. Розподіл Пуассона.

x_i	0	1	2	3	4	5
n_i	244	131	55	19	7	4

№10. Біноміальний розподіл.

x_i	0	1	2	3	4	5
n_i	3	7	22	64	19	11

ЗАДАЧА 7. За даними таблиці визначити параметри емпіричного й теоретичного розподілів і за допомогою критерію Колмогорова оцінити близькість емпіричного розподілу до нормального.

№1.

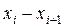
	110- 115	115- 120	120- 125	125-130	130-135	135- 140	140- 145	145- 150	150-155
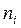
	20	62	144	170	188	176	124	74	24

№2.

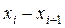
	0- 20	20- 40	40- 60	60- 80	80- 100	100- 120	120- 140	140- 160	160- 180
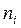
	30	80	200	400	470	360	180	50	25

№3.

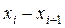
	6,65- 6,70	6,70- 6,75	6,75- 6,80	6,80- 6,85	6,85- 6,90	6,90- 6,95	6,95- 7,00	7,00- 7,05	7,05- 7,10
	5	17	24	54	52	23	18	7	4

№4.

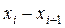
	3,0- 3,6	3,6- 4,2	4,2- 4,8	4,8- 5,4	5,4 6,0	6,0- 6,6	6,6- 7,2	7,2- 7,8	7,8- 8,4
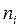
	2	8	35	43	22	15	5	4	2

№5.

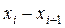
	5- 10	10- 15	15- 20	20- 25	25- 30	30- 35	35- 40	40- 45	45- 50
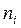
	7	8	15	18	19	14	10	6	3

№6.

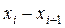
	2- 4	4- 6	6- 8	8- 10	10- 12	12- 14	14- 16	16- 18	18- 20
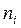
	5	15	25	30	50	28	30	20	7

№7.

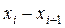
	125- 175	175- 225	225- 275	275- 325	325- 375	375- 425	425- 475	475- 525	525- 575
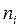
	12	24	28	28	20	16	15	12	12

№8.

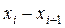
	2- 5	5- 8	8- 11	11- 14	14- 17	17- 20	20- 23	23- 26	26- 29
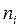
	25	25	70	120	187	130	80	20	8

№9.

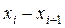
	7- 9	9- 11	11- 13	13- 15	15- 17	17- 19	19- 21	21- 23	23- 25
	40	60	75	95	125	88	80	50	37

№10.

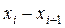
	2- 4	4- 6	6- 8	8- 10	10- 12	12- 14	14- 16	16- 18	18- 20
	7	18	35	45	50	40	30	15	10

ЗАДАЧА 8. В таблицях наведено дані, що характеризують залежність змінної y від змінної x . На підставі цих даних: а) знайти вибіркове рівняння лінійної регресії, що описує кореляційну залежність y від x; б) обчислити вибіркові коефіцієнти кореляції й детермінації.

№1

Y	X
Y	4	9	14	19	24	29
20	1	8	-	-	-	-
30	-	9	3	-	-	-
40	-	4	5	46	-	-
50	-	-	-	6	8	-
60	-	-	-	-	4	6

№2

Y	X
Y	10	15	20	25	30	35
6	3	5	4	-	-	-
8	-	2	1	3	-	-
12	-	4	40	8	-	-
16	-	-	-	5	7	5
20	-	-	-	-	7	10

№3

Y	X
Y	6	12	18	24	30	36
4	4	1	3	-	-	-
9	-	5	9	-	-	-
14	-	-	18	6	9	-
19	-	-	4	3	10	-
24	-	-	-	-	1	10

№4

Y	X
Y	5	10	15	20	25	30
6	1	4	-	-	-	-
10	-	5	9	-	-	-
14	-	-	38	6	9	-
18	-	-	4	3	10	-
22	-	-	-	-	1	10

№5

Y	X
Y	8	14	20	26	32	38
5	8	3	4	-	-	-
10	-	-	11	38	-	-
15	-	-	6	1	4	-
20	-	-	-	7	1	-
25	-	-	-	-	9	8

№6

Y	X
Y	3	8	13	18	23	28
1	1	3	6	-	-	-
6	-	4	7	-	-	-
11	-	-	50	9	1	-
16	-	-	2	8	2	-
21	-	-	-	1	3	3

№7

Y	X
Y	7	10	13	16	19	22
2	3	5	-	-	-	-
4	-	15	9	-	-	-
6	-	-	23	6	1	-
8	-	-	-	12	7	-
10	-	-	-	-	14	5

№8

Y	X
Y	2	7	12	17	22	27
20	4	1	3	-	-	-
30	-	5	6	-	-	-
40	-	-	7	40	8	-
50	-	-	-	9	1	3
60	-	-	-	-	9	4

№9

Y	X
Y	10	20	30	40	50	60
1	2	2	3	-	-	-
6	-	4	4	5	-	-
11	-	-	40	11	21	-
16	-	-	-	1	2	3
21	-	-	-	-	-	4

№10

Y	X
Y	1	4	7	10	13	16
9	7	3	-	-	-	-
13	-	10	23	5	-	-
17	-	-	5	43	8	-
21	-	-	-	-	9	6
25	-	-	-	-	-	6

ЛІТЕРАТУРА

1. Гмурман В.Е. Теория верностей и математическая статистика. Учебн. пособие для вузов. – 7-е издание – М.: Высш. шк., 1999. – 479 с.

2. Гмурман В.Е. Руководство к решению задач по теории верностей и математической статистике. Учебн. пособие для студ. вузов. – 5-е издание – М.: Высш. шк., 2000. – 400 с.

3. Ю.Д.Заворотнев, А.С.Крахмаль, Е.Б.Лещинский. Курс лекций по вероятностно-статистическим методам в психологи / Часть 1. Основы теории вероятностей и математической статистики // Учебное пособие. – Донецк: Норд-Пресс. – 275 с.

4. Практикум з теорії ймовірностей та математичної статистики: Навч. посіб. для студ. вищ. навч. зал. / Р.К.Чорней, О.Ю.Дюженкова, О.Б.Жильцов та ін.; За ред. Р.К.Чорнея. – К.: МАУП, 2003. – 328 с.

5. Теория верностей и математическая статистика. Учебн. пособие для вузов/ Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фурман; Под ред.. проф. Н.Ш.Кремера. – М.: ЮНИТИ, 2000. – 407 с.

6. Жлуктенко B.I. Наконєчний С.І. Теорія ймовірностей із елементами математичної статистики. – К., УМКВО, 1991.

7. Жлуктенко B.I., Наконєчний C.I. Практикум з курсу "Теорія ймовірностей і математична статистика". – К.: КІНГ, 1991.

8. Заворотнєв Ю.Д., Крахмаль А.С., Маєвський B.C. Теорія ймовірностей. Навчальний посібник. Макіївка, 1996.

9. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1971.

ДОДАТОКИ

Таблиця 1. Значення функції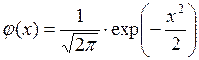


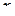
0,00 01 02 03 04 05 06 07 08 09 0,10 11 12 13 14 15 16 17 18 19 0,20 21 22 23 24 25 26 27 28 29 0,30 31 32 33 34 35 36 37 38 39	0,39894 39892 39886 39876 39862 39844 39822 39797 39767 39733 39695 39654 39608 39559 39505 39448 39387 39322 39253 39181 39104 39024 38940 38853 38762 38667 38568 38466 38361 38251 38139 38023 37903 37780 37654 37524 37391 37255 37115 36973	0,40 41 42 43 44 45 46 47 48 49 0,50 51 52 53 54 55 56 57 58 59 0,60 61 62 63 64 65 66 67 68 69 0,70 71 72 73 74 75 76 77 78 79	0,36827 36678 36526 36371 36213 36053 35889 35723 35553 35381 35207 35029 34849 34667 34482 34494 34105 33912 33718 33521 33322 33121 32918 32713 32506 32297 32086 31874 31659 31443 31225 31006 30785 30563 30339 30114 29887 29659 29430 29200	0,80 81 82 83 84 85 86 87 88 89 0,90 91 92 93 94 95 96 97 98 99 1,00 01 02 03 04 05 06 07 08 09 1,10 11 12 13 14 15 16 17 18 19	0,28969 28737 28504 28269 28034 27798 27562 27324 27086 26848 26609 26369 26129 25888 25647 25647 25164 24923 24681 24439 0,24197 23955 23713 23471 23230 22988 22747 22506 22265 22025 21785 21546 21307 21069 20831 20594 20357 20121 19886 19652	1,20 21 22 23 24 25 26 27 28 29 1,30 31 32 33 34 35 36 37 38 39 1,40 41 42 43 44 45 46 47 48 49 1,50 51 52 53 54 55 56 57 58 59	0,19419 19186 18954 18724 18494 18265 18637 17810 17585 17360 17137 16915 16694 16474 16256 16038 15822 15608 15395 15183 14973 14764 14556 14350 14146 13943 13742 13542 13944 13147 0,12952 12758 12566 12376 12188 12001 11816 11632 11450 11270	1,60 61 62 63 64 65 66 67 68 69 1,70 71 72 73 74 75 76 77 78 79 1,80 81 82 83 84 85 86 87 88 89 1,90 91 92 93 94 95 96 97 98 99	0,11092 10915 10741 10567 10396 10226 10059 09893 09728 09566 09405 09246 09089 08933 08780 08628 08478 08329 08183 08038 07895 07754 07614 07477 07341 07206 07074 06943 06814 06687 06562 06438 06316 06195 06077 05959 05844 05730 05618 05508	2,00 01 02 03 04 05 06 07 08 09 2,10 11 12 13 14 2,15 16 17 18 19 2,20 21 22 23 24 25 26 27 28 29 2,30 31 32 33 34 35 36 37 38 39	0,05399 05292 05186 05082 04980 04879 04780 04682 04586 04491 04398 04307 04217 04128 04041 03955 03871 03788 03706 03626 03547 03470 03394 03319 03246 03174 03103 03034 02965 02898 02833 02768 02705 02643 02582 02522 02463 02406 02349 02294

Продовження таблиці 1 значень функції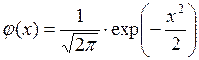


2,40 41 42 43 44 45 46 47 48 49 2,50 51 52 53 54 55 56 57 58 59 2,60 61 62 63 64 65 66 67 68 69	0,02239 02186 02134 02083 02033 01984 01936 01888 01842 01797 01750 01709 01667 01625 01585 01545 01506 01468 01431 01394 01358 01323 01289 01256 01223 01191 01160 01130 01100 01071	2,70 71 72 73 74 75 76 77 78 79 2,80 81 82 83 84 85 86 87 88 89 2,90 91 92 93 94 95 96 97 98 99	0,01042 01014 00987 00961 00935 00909 00885 00861 00837 00814 00792 00770 00748 00727 00707 00687 00668 00649 00631 00613 00595 00578 00562 00545 00530 00514 00499 00485 00470 00457	3,00 01 02 03 04 05 06 07 08 09 3,10 11 12 13 14 15 16 17 18 19 3,20 21 22 23 24 25 26 27 28 29	0,00443 00430 00417 00405 00393 00381 00370 00358 00348 00337 00327 00317 00307 00298 00288 00279 00271 00262 00254 00246 00238 00231 00224 00216 00210 00203 00196 00190 00184 00178	3,30 31 32 33 34 35 36 37 38 39 3,40 41 42 43 44 45 46 47 48 49 3,50 51 52 53 54 55 56 57 58 59	0,00172 00167 00161 00156 00151 00146 00141 00136 00132 00127 00123 00119 00115 00111 00107 00104 00100 06097 00094 00090 00087 00084 00081 00079 00076 00073 00071 00068 00066 00063	3,60 61 62 63 64 65 66 67 68 69 8,70 71 72 73 74 75 76 77 78 79 3,80 81 82 83 84 85 86 87 88 89	0,00061 00059 00057 00055 00053 00051 00049 00047 00046 00044 00042 00041 00039 00038 00037 00035 00034 00033 00031 00030 00029 00028 00027 00026 00025 00024 00023 00022 00021 00021	3,90 91 92 93 94 95 96 97 98 99	0,00020 00019 00018 00018 00017 00016 00016 00015 00014 00014

Таблиця 2. Значення функції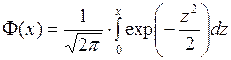


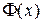
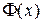
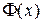
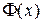
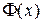
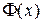
0,00 01 02 03 04 05 06 07 08 09 0,10 11 12 13 14 15 16 17 18 19 0,20 21 22 23 24 25 26 27 28 29 0,30 31 32 33 34 35 36 37 38 39	0,00000 00399 00798 01197 01595 01994 02392 02790 03188 03586 03983 04380 04776 05172 05567 05962 06356 06749 07142 07535 07926 08317 08706 09095 09483 09871 10257 10642 11026 11409 11791 12172 12552 12930 13307 13683 14058 14431 14803 15173	0,40 41 42 43 44 45 46 47 48 49 0,50 51 52 53 54 55 56 57 58 59 0,60 61 62 63 64 65 66 67 68 69 0,70 71 72 73 74 75 76 77 78 79	0,15542 15910 16276 16640 17003 17364 17724 18082 18439 18793 19146 19497 19847 20194 20540 20884 21226 21566 21904 22240 22575 22907 23237 23565 23891 24215 24537 24857 25175 25490 25804 26115 26424 26730 27035 27337 27637 27935 28230 28524	0,80 81 82 83 84 85 86 87 88 89 0,90 91 92 93 94 95 96 97 98 99 1.00 01 02 03 04 05 06 07 08 09 1,10 11 12 13 14 15 16 17 18 19	0,28814 29103 29389 29673 29955 30234 30511 30785 31057 31327 31594 31859 32121 32381 32639 32894 33147 33398 33646 33891 34134 34375 34614 34850 35083 35314 35543 35769 35993 36214 36433 36650 36864 37076 37286 37493 37698 37900 38100 38298	1,20 21 22 23 24 25 26 27 28 29 1,30 31 32 33 34 35 36 37 38 39 1,40 41 42 43 44 45 46 47 48 49 1,50 51 52 53 54 55 56 57 58 59	0,38493 38686 38877 39065 39251 39435 39617 39796 39973 40147 40320 40490 40658 40824 40988 41149 41309 41466 41621 41774 41924 42073 42220 42364 42507 42647 42786 42922 43056 43189 43319 43448 43574 43699 43822 43943 44062 44179 44295 44408	1,60 61 62 63 64 65 66 67 68 69 1,70 71 72 73 74 75 76 77 78 79 1,80 81 82 83 84 85 86 87 88 89 1,90 91 92 93 94 95 96 97 98 99	0,44520 44630 44738 44845 44950 45053 45154 45254 45352 45449 45543 45637 45728 45818 45907 45994 46080 46164 46246 46327 46407 46485 46562 46638 46712 46784 46856 46926 46995 47062 47128 47193 47257 47320 47381 47441 47500 47558 47615 47670	2,00 01 02 03 04 05 06 07 08 09 2,10 11 12 13 14 15 16 17 18 19 2,20 21 22 23 24 25 26 27 28 29 2,30 31 32 33 34 35 36 37 38 39	47725 47778 47831 47882 47932 47932 48030 48077 48124 48169 48214 48257 48300 48311 48382 48422 48461 48500 48537 48574 48610 48645 48679 48713 48745 48778 48809 48840 48870 48899 48928 48956 48983 49010 49036 49061 49086 49111 49134 49158

Продовження таблиці 2 значень функції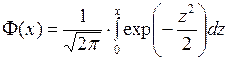


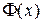
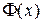
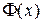
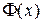
2,40 41 42 43 44 45 46 47 48 49 2,50 51 52 53 54 55 56 57 58 59	0,49180 49202 49224 49245 49266 49286 49305 49124 49343 49361 0,49379 49396 49413 49430 49446 49461 49477 49492 49506 49520	2,60 61 62 63 64 65 66 67 68 69 2,70 71 72 73 74 75 76 77 78 79	0,49534 49547 49560 49573 49585 49598 49609 49621 49632 49643 0,49653 49664 49674 49683 49693 49702 49711 49720 49728 49736	2,80 81 82 83 84 85 86 87 88 89 2,90 91 92 93 94 95 96 97 98 99	0,49744 49752 49760 49767 49774 49781 49788 49795 49801 49807 0,49813 49819 49825 49831 49836 49841 49846 49851 49856 49861	3,0 1 2 3 4 5 6 7 8 9 4,0 4,5 5,0	0,40865 49903 49931 49952 49966 49977 49984 49989 49993 49995 499968 499997 499999

Таблиця 3. Критичні точки розподілу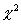

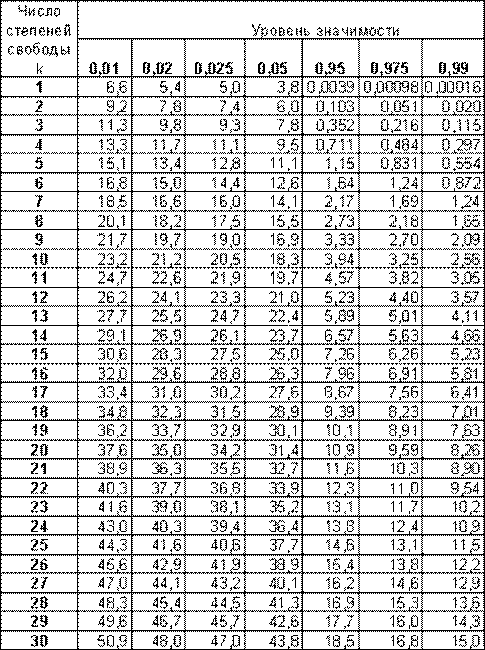
Таблиця 4. Значення функції Колмогорова.


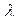
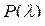
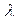
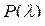
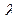
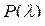
1	2	3	4	5	6
0,33 0,34 0,35 0,35 0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 0,80	– – 0,0001 0,0002 0,0003 0,0005 0,0008 0,0013 0,0019 0,0028 0,0040 0,0055 0,0074 0,0097 0,0186 0,0160 0,0200 0,0247 0,0300 0,0361 0,0428 0,0503 0,0585 0,0674 0,0772 0,0876 0,0987 0,1104 0,1228 0,1357 0,1492 0,1632 0,1778 0,1927 0,2080 0,2236 0,2396 0,2558 0,2722 0,2888 0,3055 0,3223 0,3301 0,3560 0,3728 0,3896 0,4064 0,4230 0,4395 0,4559	0,81 0,82 0,83 0,84 0,85 0,85 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 1,30	0,4720 0,4880 0,5038 0,5194 0,5347 0,5497 0,5645 0,5791 0,5933 0,6073 0,6209 0,6343 0,6473 0,6601 0,6725 0,6846 0,6994 0,7079 0,7191 0,7300 0,7406 0,7508 0,7608 0,7704 0,7798 0,7889 0,7976 0,8061 0,8143 0,8222 0,8300 0,8374 0,8445 0,8514 0,8580 0,8644 0,8706 0,8765 0,8829 0,8878 0,8930 0,8981 0,9030 0,9076 0,9121 0,9164 0,9206 0,9245 0,9283 0,9319	1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 1,59 1,60 1,61 1,63 1,65 1,80 1,85 1,90 1,95 2,00 2,05 2,10 2,15 2,20 2,25 2,30 2,35 2,40 2,50 3,00	0,9354 0,9387 0,9418 0,9448 0,9478 0,9505 0,9531 0,9557 0,9580 0,9603 0,9625 0,9646 0,9665 0,9684 0,9702 0,9718 0,9734 0,9750 0,9764 0,9778 0,9791 0,9803 0,9815 0,9826 0,9836 0,9846 0,9855 0,9864 0,9873 0,9880 0,9914 0,9938 0,9956 0,9969 0,9979 0,9985 0,9990 0,9993 0,9996 0,9997 0,9998 0,9998 0,9999 0,99995 0,99997 0,99998 0,99999 0,99999

Таблиця 5 . Значення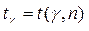

n	g			n	g
n	0,95	0,99	0,999	n	0,95	0,99	0,999
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19	2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10	4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88	8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92	20 25 30 35 40 45 50 60 70 80 90 100 120 ¥	2,093 2,064 2,045 2,032 2,023 2,016 2,009 2,001 1,996 1,991 1,987 1,984 1,980 1,960	2,861 2,797 2,756 2,720 2,708 2,692 2,679 2,662 2,649 2,640 2,633 2,627 2,617 2,576	3,883 3,745 3,659 3,600 3,558 3,527 3,502 3,464 3,439 3,418 3,403 3,392 3,374 3,291

Таблиця 6. Значення критерію Фішера (F-критерію) для рівню значимості p = 0,05. f₁ – число ступіней свободи більшої дисперсії, f₂ - число ступіней свободи меншої дисперсії

	f ₁
f ₂	1	2	3	4	5	6	7	8	9	10	15
1	161.45	199.50	215.71	224.58	230.16	233.99	236.77	238.88	240.54	241.88	245.95
2	18.51	19.00	19.16	19.25	19.30	19.33	19.35	19.37	19.38	19.40	19.43
3	10.13	9.55	9.28	9.12	9.01	8.94	8.89	8.85	8.81	8.79	8.70
4	7.71	6.94	6.59	6.39	6.26	6.16	6.09	6.04	6.00	5.96	5.86
5	6.61	5.79	5.41	5.19	5.05	4.95	4.88	4.82	4.77	4.74	4.62
6	5.99	5.14	4.76	4.53	4.39	4.28	4.21	4.15	4.10	4.06	3.94
7	5.59	4.74	4.35	4.12	3.97	3.87	3.79	3.73	3.68	3.64	3.51
8	5.32	4.46	4.07	3.84	3.69	3.58	3.50	3.44	3.39	3.35	3.22
9	5.12	4.26	3.86	3.63	3.48	3.37	3.29	3.23	3.18	3.14	3.01
10	4.96	4.10	3.71	3.48	3.33	3.22	3.14	3.07	3.02	2.98	2.85
11	4.84	3.98	3.59	3.36	3.20	3.09	3.01	2.95	2.90	2.85	2.72
12	4.75	3.89	3.49	3.26	3.11	3.00	2.91	2.85	2.80	2.75	2.62
13	4.67	3.81	3.41	3.18	3.03	2.92	2.83	2.77	2.71	2.67	2.53
14	4.60	3.74	3.34	3.11	2.96	2.85	2.76	2.70	2.65	2.60	2.46
15	4.54	3.68	3.29	3.06	2.90	2.79	2.71	2.64	2.59	2.54	2.40
16	4.49	3.63	3.24	3.01	2.85	2.74	2.66	2.59	2.54	2.49	2.35
17	4.45	3.59	3.20	2.96	2.81	2.70	2.61	2.55	2.49	2.45	2.31
18	4.41	3.55	3.16	2.93	2.77	2.66	2.58	2.51	2.46	2.41	2.27
19	4.38	3.52	3.13	2.90	2.74	2.63	2.54	2.48	2.42	2.38	2.23
2 0	4.35	3.49	3.10	2.87	2.71	2.60	2.51	2.45	2.39	2.35	2.20

Методичні вказівки

Методичні вказівки до виконання індивідуальних робіт з дисципліни “Теорія ймовірностей та математична статистика” для студентів спеціальності “Соціологія”. Частина 2.

Укладачі: