Основні поняття
Нехай потрібно досліджувати будь-яку ознаку, яка притаманна великій групі однотипних виробів (наприклад: розмір деталей даного типу, вагу виробу тощо)
Сукупність значень ознаки усіх N виробів даного типу називається генеральною сукупністю.
Вибірковою сукупністю, або просто вибіркою, називають сукупність випадково відібраних об'єктів. Ці вибірки реально спостерігаються в експерименті. Кількість цих даних називається об'ємом вибірки. Теоретично вибірка є сукупність незалежних однаково розподілених випадкових величин, розподіл яких співпадає з розподілом генеральної сукупності.
Вибірковий метод полягає в тому, що з генеральної сукупності береться вибірка обсягу п (причому п << N) і визначаються характеристики вибірки, що приймаються в якості наближених значень відповідних характеристик генеральної сукупності.
Вибірки бувають повторні (з поверненням відібраного елемента до генеральної сукупності) та безповторпі (без повернення).
Вибірки розрізняються за способом відбору: простий випадковий відбір (елементи відбирають по одному з генеральної сукупності), типовий відбір (елементи відбирають з деякої частини генеральної сукупності), механічний відбір (елементи відбирають по одному з кожної частини генеральної сукупності), серійний відбір (елементи відбирають серіями).
Різні елементи вибірки називаються варіантами і позначаються 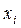 . Число, що показує, скільки разів зустрічається варіанта в даній вибірці, називається частотою і позначається
. Число, що показує, скільки разів зустрічається варіанта в даній вибірці, називається частотою і позначається 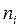 . Сума частот дорівнює об'єму вибірки (загальному числу спостережень
. Сума частот дорівнює об'єму вибірки (загальному числу спостережень 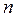 ). Відношення частоти до об'єму вибірки називається відносною частотою, тобто
). Відношення частоти до об'єму вибірки називається відносною частотою, тобто 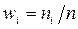 . Сума відносних частот дорівнює одиниці.
. Сума відносних частот дорівнює одиниці.
Для проведення статистичного аналізу необхідно вибірки, що розглядаються представити у зручному і сприйнятливому вигляді. Для цього складають статистичний розподіл вибірки.
Припустимо, що вивчається деяка випадкова величина Х, закон розподілу якої невідомий. Над випадковою величиною Х проводиться ряд незалежних спостережень (вимірів). Результати вимірів подають у вигляді таблиці, що складається з двох рядків, у першому із яких указуються номера вимірів i, а у другому – результати вимірів хi :
| і | 1 | 2 | … | п |
| xi | x1 | x2 | … | xn |
Таблицю, що вміщує номера і результати вимірів, називають рядом варіант або статистичним рядом.
Варіаційним рядом вибірки називають засіб її запису, при якому елементи хi (варіанти) розташовані за розміром, тобто записуються в зростаючому порядку. Різниця між максимальним і мінімальним елементами вибірки називається розмахом вибірки. Рівні між собою члени нумеруються в довільному порядку. Ці дії називаються рангуванням статистичних даних.
Нехай у вибірці обсягу п елемент xi зустрічається ni разів. Число ni називається частотою елемента xi. При цьому 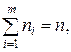 де т – число різноманітних варіант ni..
де т – число різноманітних варіант ni..
Відношення 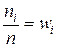 називаються відносними частотами і
називаються відносними частотами і 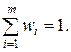
Статистичним розподілом (розподілом частот) вибірки називають перелік варіант і відповідних їм частот.
Його можна також записати у вигляді послідовності інтервалів і відповідних їм частот. У якості частоти, що відповідає інтервалу, приймають суму частот, що потрапили в цей інтервал, причому якщо при угрупованні значень що спостерігаються, маємо значення, що у точності лежить на межі двох інтервалів, то варто додати до числа ni однієї і іншої груп по 1/2 частоти, що відповідає даному значенню.
З метою наочності будують різноманітні графіки статистичного розподілу і, зокрема, полігон і гістограму.
Полігоном частот називається ломана, відрізки якої з'єднують точки з координатами (x1, n1),...,( xm, nm).
Полігоном відносних частот називають ломану, що з'єднує точки з координатами (x1, w1),...,( xm, wm).
У випадку неперервноі ознаки (наприклад, дальність польоту снаряда) або при великому числі значень ознаки доцільно будувати гістограму частот, для чого інтервал, у якому укладені всі значення ознаки, розбивають на декілька часткових інтервалів довжиною h і знаходять для кожного i-го часткового інтервалу частоту ni, що дорівнює сумі частот варіант, що потрапили в i-й інтервал.
Гістограмою частот називають ступінчасту фігуру, що складається з прямокутників, основами яких є часткові інтервали довжиною h, а висоти дорівнюють відношенню 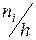 (щільність частоти). Площа i-го часткового прямокутника дорівнює
(щільність частоти). Площа i-го часткового прямокутника дорівнює 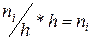 - сумі частот варіант i-го інтервалу; отже, площа гістограми частот дорівнює сумі всіх частот, тобто обсягу вибірки.
- сумі частот варіант i-го інтервалу; отже, площа гістограми частот дорівнює сумі всіх частот, тобто обсягу вибірки.
Гістограмою відносних частот називають ступінчасту фігуру, що складається з прямокутників, основами яких є часткові інтервали довжиною h 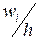 а висоти дорівнюють відношенню
а висоти дорівнюють відношенню 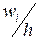 (щільність відносної частоти). Площа гістограми відносних частот дорівнює сумі площ усіх прямокутників, тобто
(щільність відносної частоти). Площа гістограми відносних частот дорівнює сумі площ усіх прямокутників, тобто
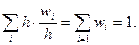
Емпіричною функцією розподілу називають функцію  , яка визначає для кожного значення х відносну частоту події Х<х, тобто
, яка визначає для кожного значення х відносну частоту події Х<х, тобто 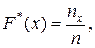 де
де 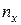 – число варіант, менших х, п - обсяг вибірки.
– число варіант, менших х, п - обсяг вибірки.
З визначення  випливають такої її властивості:
випливають такої її властивості:
1) значення емпіричної функції належать відрізку [0;1];
2)  - функція , що не убуває;
- функція , що не убуває;
3) якщо x1 – найменша варіанта, то 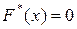 при
при 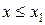 ;
;
якщо хk - найбільша варіанта, то 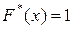 при х > хk;
при х > хk;
Емпіричну функцію розподілу 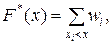 можна також визначити як суму відносних частот варіант, менших х.
можна також визначити як суму відносних частот варіант, менших х.
ПРИКЛАД 1 . При обстеженні студентів першого курсу за віком були зафіксовані наступні дані (табл. 1). Побудувати полігон розподілу.
Таблиця 1.
Розподіл студентів першого курсу за віком
| Вік студентів (варіанты xi) | Число студенів з даним віком (частоти ni) | Частости (fi) | |
| відносні | в % | ||
| 17 18 19 20 21 22 23 | 2 15 14 6 6 5 2 | 0,04 0,30 0,28 0,12 0,12 0,10 0,04 | 4 30 28 12 12 10 4 |
| Разом | 50 | 1,0 | 100 |
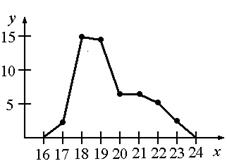
| У прямокутній системі координат на горизонтальній осі відкладаємо значення ознаки (вік студентів), а на вертикальній осі – частоти (число студентів з даним віком). Отримані крапки з'єднаємо відрізками прямої. Для того щоб фігура була замкнутої, уведемо додатково нові значення ознаки (16 років, 24 роки); відповідні їм частоти, природно, дорівнюють нулю. У результаті одержимо полігон розподілу студентів за віком (мал. 1). |
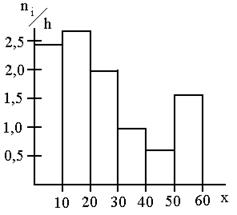
ПРИКЛАД 2. Побудуємо гістограму розподілу душ за розміром прирізки в Бєльському повіті Смоленської губернії за даними табл.2. (За браком додаткових даних при побудові графіка скористаємося припущенням, що величина останнього відкритого інтервалу дорівнює величині попереднього).
Таблиця 2
Розподіл душ за розміром прирізки в Бєльському повіті Смоленської губернії.
|
|
Як уже відзначалося, для інтервального ряду також можна побудувати полігон розподілу. Для цього за значення ознаки приймають середини інтервалів і для отриманого дискретного ряду звичайним способом будують полігон. Результати такої побудови зображені на рис 2.
Дата: 2019-02-02, просмотров: 832.