Нехай генеральна сукупність Х має нормальний розподіл, і потрібно перевірити припущення про те, що її математичне сподівання дорівнює деякому числу а₀. Розглянемо дві можливості.

1) Відома дисперсія σ² генеральної сукупності. Тоді за вибіркою обсягу п знайдемо вибіркове середнє 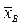 і перевіримо нульову гіпотезу Н₀: М(Х) = а₀.

З огляду на те, що вибіркове середнє 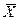 є незміщеною оцінкою М(Х), тобто М(  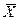) = М(Х), можна записати нульову гіпотезу так: М(  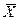) = а₀. Для її перевірки оберемо критерій

.

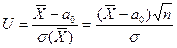Це випадкова величина, що має нормальний розподіл, причому, якщо нульова гіпотеза справедлива, тобто М(U) = 0, σ(U) = 1.

Виберемо критичну область у залежності від виду конкуруючої гіпотези:

– якщо Н₁: М( 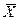)≠а₀, то і_кр: 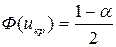, критична область двостороння, 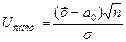, і, якщо |U_спост| < u_кр, то нульова гіпотеза приймається; якщо |U_спост| > u_кр, то нульова гіпотеза відкидається.

– якщо Н₁: М( 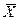)>а₀, то і_кр: 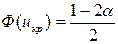, критична область правобічна, і, якщо U_спост < u_кр, то нульова гіпотеза приймається; якщо U_спост> u_кр, то нульова гіпотеза відкидається.

– якщо Н₁: М( 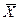)<а₀, то і_кр: 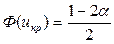, критична область лівостороння, і, якщо U_спост > – u_кр, то нульова гіпотеза приймається; якщо U_спост<–u_кр, то нульова гіпотеза відкидається.

2) Дисперсія генеральної сукупності невідома.

У цьому випадку виберемо як критерій випадкову величину

 ,

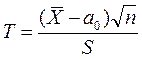де S – виправлене середньоквадратичне відхилення. Така випадкова величина має розподіл Стьюдента з k=n–1 ступенями свободи. Розглянемо ті ж, що й у попередньому випадку, конкуруючі гіпотези та відповідаючи їм критичні області. Попередньо обчислимо значення критерію, що спостерігається:

.

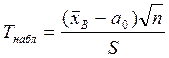Нехай Н₁: М( 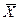 ) ≠ а₀, то критична точка t_{двуст.кр.} знаходиться за таблицею критичних точок розподілу Стьюдента (табл. додатка) за відомим α і k=n–1:

– якщо | T_спост | < t_{двост.кр.}, то нульова гіпотеза приймається;

– якщо | T_спост | > t_{двост.кр.}, то нульова гіпотеза відкидається.

Нехай Н₁: М( 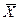 ) > а₀, то по відповідній таблиці знаходять t_{правост.кр.}(α, k) – критичну точку правобічної критичної області. Нульова гіпотеза приймається, якщо T_спост < t_{правост.кр.}.

При конкуруючій гіпотезі Н₁: М( 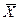)<а₀ критична область є лівосторонньої, і нульова гіпотеза приймається за умови T_спост> – t_{правост.кр.}. Якщо T_спост < – t_{правост.кр}, нульову гіпотезу відкидають.

2.4. Критерій для перевірки гіпотези про порівняння двох дисперсій

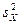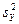Нехай маються дві нормально розподілені генеральні сукупності Х и Y. З них витягнуті незалежні вибірки обсягів відповідно п₁ і п₂, за якими обчислено виправлені вибіркові дисперсії  і . Потрібно при заданому рівні значимості α перевірити нульову гіпотезу Н₀: D(X)=D(Y) про рівність дисперсій розглянутих генеральних сукупностей. З огляду на незміщеність виправлених вибіркових дисперсій, можна записати нульову гіпотезу так:

Н₀: М ( 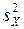 ) = М (  ).

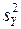Звичайно, виправлені дисперсії, обчислені по вибірках, звичайно виявляються різними. При перевірці гіпотези з'ясовується, чи є це розходження незначущим і обумовленої випадковими причинами (у випадку прийняття нульової гіпотези) чи воно є наслідком того, що самі генеральні дисперсії різні.

За критерій приймемо випадкову величину

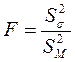
– відношення більшої вибіркової дисперсії до меншого. Вона має розподіл Фішера-Снедекора зі ступенями свободи k₁=n₁–1 і k₂=n₂–1, де п₁ – обсяг вибірки, за якою обчислена велика виправлена дисперсія, а п₂ – обсяг другої вибірки. Розглянемо два види конкуруючих гіпотез.

Нехай Н₁: D(X)>D(Y). Значенням критерію, що спостерігається, буде відношення більшої з виправлених дисперсій до меншого 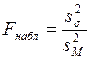. По таблиці критичних точок розподілу Фишера-Снедекора (табл.. додатка) можна знайти критичну точку F_спост (α; k₁; k₂). При F_спост<F_кр нульова гіпотеза приймається, при F_спост>F_кр відкидається.

Якщо Н₁: D(X) ≠ D(Y), то критична область є двосторонньої і визначається нерівностями F<F₁, F>F₂, де р(F<F₁) = р(F>F₂) = α/2. При цьому досить знайти праву критичну крапку F₂=F_кр( 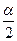, k₁, k₂). Тоді при F_спост<F_кр нульова гіпотеза приймається, при F_спост>F_кр відкидається.