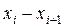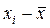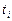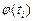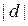Достоїнством критерію Пірсона є його універсальність: з його допомогою можна перевіряти гіпотези про різні закони розподілу.
1. Перевірка гіпотези про нормальний розподіл.
Нехай отримана вибірка досить великого обсягу п з великою кількістю різних значень варіант. Для зручності її обробки розділимо інтервал від найменшого до найбільшого зі значень варіант на s рівних частин і будемо вважати, що значення варіант, що потрапили до кожного інтервалу, приблизно дорівнюють числу, що задає середину інтервалу. Підрахувавши число варіант, що потрапили в кожен інтервал, складемо так називану згруповану вибірку:
Варіанти х1 х2 … хs
Частоти п1 п2 … пs ,
де хi – значення середин інтервалів, а пi – число варіант, що потрапили в i-й інтервал (емпіричні частоти).
По отриманим даним можна обчислити вибіркове середнє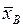 
і вибіркове середньоквадратичне відхилення σВ. Перевіримо припущення, що генеральна сукупність розподілена за нормальним законом з параметрами M(X)= 
, D(X)= 
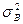. Тоді можна знайти кількість чисел з вибірки обсягу п, що повинне виявитися в кожнім інтервалі при цьому припущенні (тобто теоретичні частоти). Для цього по таблиці значень функції Лапласа знайдемо імовірність влучення в i-й інтервал:
,
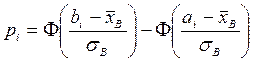де аi і bi – границі i-го інтервалу. Помноживши отримані імовірності на обсяг вибірки n, знайдемо теоретичні частоти: пi=n·pi. Наша мета – порівняти емпіричні і теоретичні частоти, що, зазвичай, відрізняються друг від друга, і з'ясувати, чи є ці розходження несуттєвими (що не спростовують гіпотезу про нормальний розподіл досліджуваної випадкової величини), чи вони настільки великі, що суперечать цій гіпотезі. Для цього використовується критерій у виді випадкової величини
.
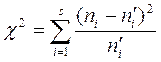Зміст її очевидний: сумуються відношення квадратів відхилень емпіричних від теоретичних частот до відповідних теоретичних частот. Можна довести, що поза залежністю від реального закону розподілу генеральної сукупності закон розподілу випадкової величини при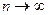 
прямує до закону розподілу 
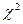з числом ступенів свободи k=s–1–r, де r – число параметрів передбачуваного розподілу, оцінених за даними вибірки. Нормальний розподіл характеризується двома параметрами, тому k=s–3. Для обраного критерію будується правобічна критична область, обумовлена умовою
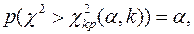
де α – рівень значимості. Отже, критична область задається нерівністю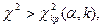 
а область прийняття гіпотези – 
.
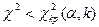Отже, для перевірки нульової гіпотези Н0: генеральна сукупність розподілена нормально – потрібно обчислити по вибірці значення критерію, що спостерігається:
,
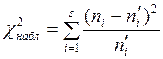а за таблицею критичних точок (таблиця 3 Додатка) розподілу χ2 знайти критичну крапку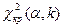 
, використовуючи відомі значення α і k=s–3. Якщо 
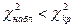– нульову гіпотезу приймають, при 
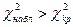неї відкидають.
ПРИКЛАД 8. Отримано такий розподіл 100 робочих цехів за продуктивністю в звітному році (у відсотках до попереднього року):
Таблиця 6
| Продуктивність у звітному році (у % до попереднього року) | 94- 104 | 104-114 | 114-124 | 124-134 | 134-144 | Разом |
| Кількість робітників | 6 | 20 | 45 | 27 | 6 | 100 |
На рівні значимості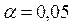 
перевірити гіпотезу про нормальний розподіл випадкової величини X – продуктивність робітників – за допомогою критерію 
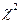Пирсона. Побудувати на одному рисунку гістограму емпіричного розподілу і відповідну нормальну криву.
РІШЕННЯ. Параметри теоретичного нормального закону розподілу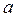 
і 
, що є відповідно математичним сподіванням і дисперсією випадкової величини X, невідомі, тому заміняємо їх "найкращими" оцінками за вибіркою – незміщеними і обгрунтованими оцінками, відповідно, вибірковою середньою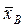 
і "виправленою" вибірковою дисперсією 
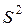. Тому що число спостережень ( 
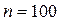) досить велико, то замість виправленої 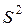можна взяти "звичайну" вибіркову дисперсію 
.
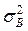Знайдемо вибіркову середню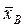 
(див. метод добутків):
і вибіркову дисперсію (див. метод добутків):
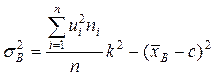
Для цього складемо розрахункову табл. 7 при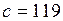 
і 
.
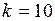Таблиця 7
| Вироблення в звітному році (%) | Середина інтервалу xi | Кількість студентів ni |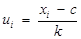 
| 
| 
|
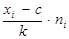
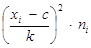
| 94-104 | 99 | 6 | -2 | -12 | 24 |
| 104-114 | 109 | 20 | -1 | -20 | 20 |
| 114-124 | 119 | 45 | 0 | 0 | 0 |
| 124-134 | 129 | 27 | 1 | 27 | 27 |
| 134-144 | 139 | 2 | 2 | 4 | 8 |
| Сума | 100 | -1 | 79 |
Тоді вибіркова середня
.
Вибіркова дисперсія
.
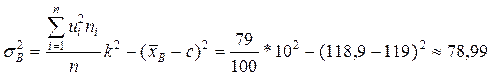Таким чином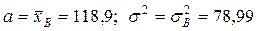 
.
Тоді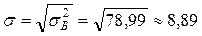 
.
Тому що випадкова величина має нормальний розподіл, то для розрахунку імовірностей улучення випадкової величини X в інтервал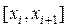 
, де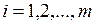 
, використовуємо функцію Лапласа у відповідності з властивостями нормального розподілу:
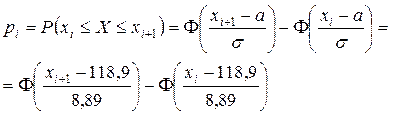
Нормальний розподіл визначений на всій числовій осі, тобто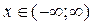 
, тому при перебуванні ймовірностей влучення випадкової величини X в інтервал 
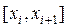для всіх значень випадкової величини X застосовується зазначена вище формула, за винятком крайніх значень, тобто значень 
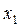і 
.
І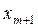мовірність улучення випадкової величини X в інтервал 
визначається наступною формулою
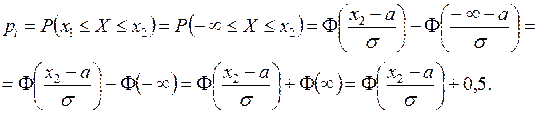
Імовірність улучення випадкової величини X в інтервал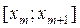 
визначається наступною формулою:
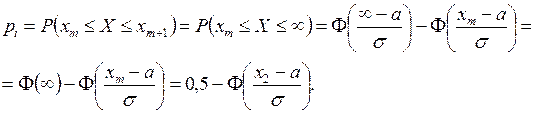
Таким чином, у нашому прикладі одержимо:
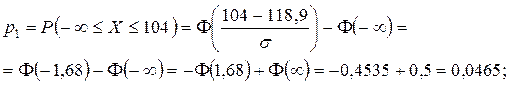
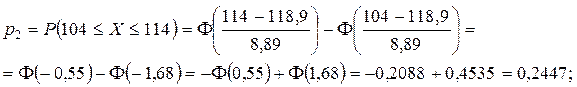
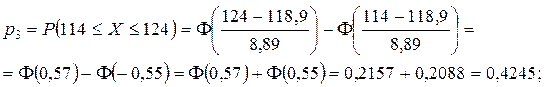
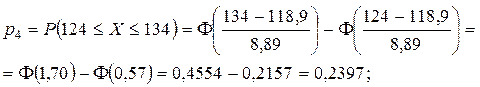
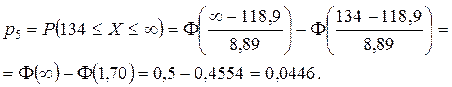
Запишемо в табл. 8 початкові дані й знайдені ймовірності. Обчислимо в табл. 8 теоретичні частоти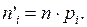 
Таблиц я 8
| i | Інтервал
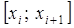
| Емпіричні частоти
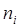
| Ймовірності
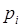
| Теоретичні частоти,
| 
|
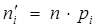
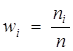
| 1 | 94 – 104 | 6 | 0,0465 | 4,65 | 0,06 |
| 2 | 104 – 114 | 20 | 0,2447 | 24,47 | 0,2 |
| 3 | 114 – 124 | 45 | 0,4245 | 42,45 | 0,45 |
| 4 | 124 – 134 | 27 | 0,2397 | 23,97 | 0,27 |
| 5 | 134 – 144 | 2 | 0,0446 | 4,46 | 0,02 |
| S | 100 |
Так як в останньому (п’ятому) інтервалі число спостережень менш п'яти, то є сенс для застосування критерію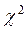 
Пирсона об'єднати останній інтервал з попереднім (як для емпіричних, так й для теоретичних частот), вважаємо при обчисленні 
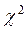емпіричну частоту, що дорівнює 27+2=29, теоретичну частоту, що дорівнює 23,97+4,46=28,43.
Для визначення вибіркової статистики
,
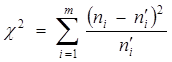складемо розрахункову таблицю 9.
Таблица 9.
| i | Емпіричні частоти
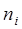
| Теоретичні частоти,
| 
| 
|
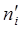
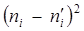
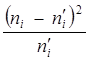
| 1 | 6 | 4,65 | 1,8225 | 0,3919 |
| 2 | 20 | 24,47 | 19,9809 | 0,8165 |
| 3 | 45 | 42,45 | 6,5025 | 0,1532 |
| 4 | 29 | 28,43 | 0,3249 | 0,0114 |
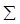
| 100 | 1,373 |
Із таблиці 9 на основі фактичних спостерігаємих значень, знаходимо статистику (вибіркову статистику)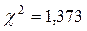 
.
Враховуючи, що число інтервалів m=4, а нормальний закон разподілу визначається r=2 параметрами, точкові оцінки яких були отримані за вибірковими даними, то число ступенів свободи k=n-m-1=4-2-1=1. Відповідне критичне значення статистики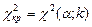 
можна знайти за таблицею "Критичні точки розподілу 
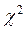" в додатку 3. Маємо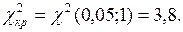 
Так як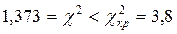 
, то гіпотеза щодо обраного теоретичного нормального закону розподілу з параметрам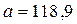и 
й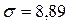 
узгоджується с дослідними даними, тобто гіпотеза приймається на заданому рівні значущості 
.
На одному рисунку побудуємо нормальну криву й гістограму. Вершина нормальної кривою має координати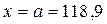 
;
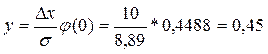
(де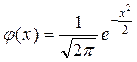 
– мала функція Лапласа, значення якої наведені в таблиці 1 додатка.
Виконавши креслення (рис. 4), можна побачити, що нормальна крива теоретичного розподілу достатньо добре "вирівнює" гістограму емпіричного розподілу.
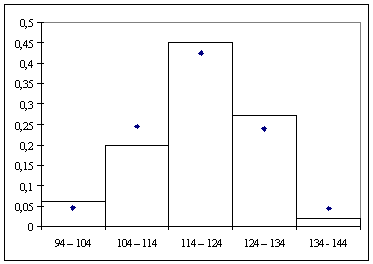
Рис.4.
ПРИКЛАД 9. У наступній таблиці представлено дані про число угод, укладених на фондовій біржі за квартал, для 517 інвесторів.
Таблиця 10
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| ni | 112 | 168 | 130 | 68 | 32 | 5 | 1 | 1 |
У першому рядку наведено кількість угод, у другому – кількість інвесторів, що уклали стільки угод за квартал.
Потрібно перевірити, використовуючи критерій Пірсона, що на рівні значущості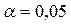 
кількість угод, що укладено одним інвестором за квартал, розподілено за законом Пуассона з параметром 
.
РОЗВ'ЯЗАННЯ. Оскільки розподіл Пуассона дискретний, у якості різних наслідків тут можна взяти самі значення випадкової величини. Помітимо, що останні два значення (6 й 7) зустрілися занадто мало разів, тому їх варто об'єднати з попереднім (5). Крім того, розподіл Пуассона не обмежений праворуч, і варто врахувати всі значення, більші 7 (які не зустрілися жодного разу). Таким чином, виберемо множину {0}, {І}, {2}, {3}, {4}, {5},[5,+¥).Тут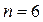 
.
Знайдемо теоретичні ймовірності за формулою розподілу Пуассона
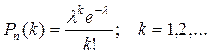
При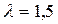 
одержуємо:
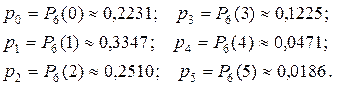
Помножимо їх на число інвесторів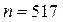 
і складемо наступну таблицю:
Таблиця 11
| k | ni | npi | ni- npi | (ni- npi)2/(npi) |
| 0 1 2 3 4 ³5 | 112 168 130 68 32 7 | 115,34 173,04 129,77 64,88 24,35 9,62 | -3,34 -5,04 0,23 3,12 7,65 -2,62 | 0,10 0,15 0,00 0,15 2,40 0,71 |
Підсумовуючи значення в останньому стовпці, одержуємо значення статистики хі-квадрат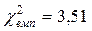 
.
По таблиці критичних точок розподілу хі-квадрат (табл.3 додатка) за рівнем значущості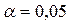 
і числу ступенів свободи 
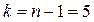(дивись зауваження) знаходимо критичну точку 
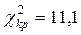. Оскільки 
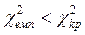, можна вважати, число угод, укладених одним інвестором за квартал, розподілено за законом Пуассона з параметром .
Зауваження. Якби значення параметра було б оцінено по самій вибірці, то число ступенів свободи було б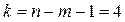 
, де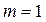 
.У цьому випадку 
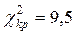, так що гіпотеза теж приймається.
Критерій Колмогорова
Критерій призначений для зіставлення двох розподілів: а) емпіричного з теоретичним; б) одного емпіричного розподілу з іншим емпіричним розподілом.
Критерій дозволяє знайти точку, у якій сума накопичених розбіжностей між двома розподілами є найбільшої й оцінити вірогідність цієї розбіжності. Найчастіше застосуються для перевірки простої гіпотези Н0 про те, що незалежні однаково розподілені випадкові величини Х1, Х2, …, Хп мають задану безупинну функцію розподілу F(x).
Гіпотези:
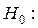розходження між двома розподілами недостовірні;
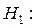розходження між двома розподілами достовірні (судячи з точки максимально накопиченої розбіжності між ними).
Обмеження критерію. Критерій вимагає досить великої вибірки при зіставленні двох емпіричних розподілів (більше чи дорівнює 50). При зіставленні емпіричного розподілу з теоретичним допускається n більше чи дорівнюючі 5.
Алгоритм розрахунку абсолютної величини різниці d між емпіричним і рівномірним розподілами.
1. Занести в таблицю найменування розрядів і відповідні їм емпіричні частоти (перший стовпець).
2. Підрахувати відносні емпіричні частоти для кожного розряду за формулою: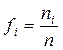 
, де: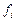 
– емпірична частота по даному розряду, n – загальна кількість спостережень. Занести результати в другий стовпець.
3. Підрахувати накопичені емпіричні частоти за формулою:
,
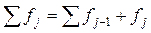де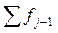 
– частота, накопичена на попередніх розрядах;
j – порядковий номер розряду;
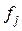– емпірична частота даного j-го розряду.
Занести результати в третій стовпець таблиці.
4. Підрахувати накопичені теоретичні частоти для кожного розряду за формулою:
,
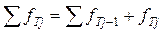де: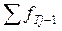 
– теоретична частота, накопичена на попередніх розрядах;
j – порядковий номер розряду;
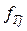– теоретична частота даного розряду. Занести результати в четвертий стовпець таблиці.
5. Обчислити різниці між емпіричними й теоретичними накопиченими частотами за кожнім розрядом.
6. Записати в п'ятий стовпець абсолютні величини отриманих різностей (без обліку їхнього знака). Позначити їх як d.
7. Визначити по п'ятому стовпці найбільшу величину різниці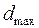 
.
8. Обчислити величину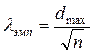 
. Виходячи з таблиць, визначити при заданому рівні надійності 
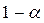зі співвідношення 
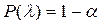табличне значення критерію 
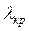. Якщо отримане емпіричне число 
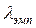перевищують критичне 
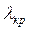– розходження достовірні.
ПРИКЛАД 9. Визначити параметри емпіричного й теоретичного розподілів та за допомогою критерію Колмогорова оцінити близькість емпіричного розподілу до нормального при рівні значимості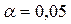 
.
Вихідні дані дано втаблиці.
Таблиця 12
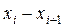
| 306- 311 | 311- 316 | 316- 321 | 321- 326 | 326- 331 | 331- 336 | 336- 341 | 341- 346 | 346- 351 | 351- 356 |
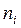
| 19 | 34 | 38 | 33 | 38 | 17 | 11 | 6 | 2 | 2 |
За допомогою методу умовних моментів визначаємо середню величину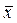 
і середньоквадратичне відхилення 
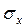. Розрахунки представлені в наступній таблиці
Таблиця 13
| 
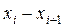
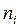
| Середина інтервалу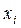 
| 
| 
| 
|
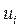
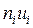
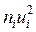
| 306-311 311-316 316-321 321-326 326-331 331-336 336-341 341-346 346-351 351-356 | 19 34 38 33 38 17 11 6 2 2 | 308,5 313,5 318,5 323,5 328,5 333,5 338,5 343,5 348,5 353,5 | -4 -3 -2 -1 0 1 2 3 4 5 | -76 -102 -76 -33 0 17 22 18 8 10 | 304 306 152 33 0 17 44 54 32 50 |
| Разом | 200 | -212 | 992 |
Умовні моменти
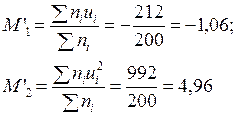
Вибіркові середня і середньоквадратичне відхилення
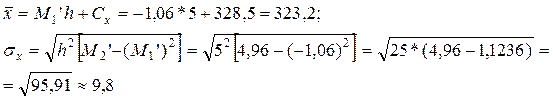
Розрахуємо теоретичні частоти (див. наступну таблицю). Для цього визначаємо нормовані відхилення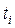 
(графа 4), по додатку встановлюємо значення функції 
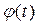(графа 5), розраховуємо теоретичні частоти по формулі
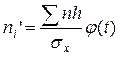
За даними розглянутого приклада
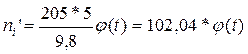
Таблица 1 4
|
|
|
|
|
|
| Уточ-нена теор. частота | Накопичена частота |
| |
| Фак-тична | Теоре-тична | ||||||||
| 296-301 301-306 306-311 311-316 316-321 321-326 326-331 331-336 336-341 341-346 346-351 351-356 | - - 19 34 38 33 38 17 11 6 2 2 | -24,7 -19,7 -14,7 -9,7 -4,7 -0,3 5,3 10,3 15,3 20,3 25,3 30,3 | -2,52 -2,01 -1,50 -0,99 -0,48 -0,03 -,54 1,05 1,56 2,07 2,58 3,10 | 0,0167 0,0529 0,1296 0,2444 0,3565 0,3988 0,3448 0,2299 0,1182 0,0468 0,0143 0,0033 | - - 13 25 36 41 35 24 12 5 1 - | 2 6 13 25 36 41 35 24 12 5 1 - | - - 19 53 91 124 162 179 190 196 198 200 | 2 8 21 46 82 123 158 182 184 199 200 200 | 2 8 2 7 9 1 4 3 4 3 2 0 |
З огляду на те, що теоретичні частоти можуть бути тільки цілими числами, округляємо їх і знаходимо суму, що дорівнює 192. Таким чином, має місце розбіжність сум теоретичних частот (192) і фактичних (200). У даному випадку така розбіжність може бути пояснено відмінністю крайніх теоретичних частот від нуля. Тому теоретичну криву треба продовжити. У нашому прикладі нормальна крива може бути продовжена убік від'ємних відхилень від середньої. Робимо розрахунок теоретичних частот для перших двох інтервалів і одержуємо значення частот, що дорівнюють 2 і 6. Далі визначаємо накопичені фактичні й теоретичні частоти. Розраховуємо різницю між ними й встановлюємо максимальну розбіжність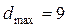 
(п'ятий інтервал). Обчислюємо величину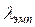 
За даними таблиці додатка знаходимо при рівні значимості 0,05
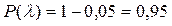табличне значення критерію 
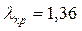. Так як 
(0,636<1,36), то гіпотеза про нормальний розподіл досліджуваної ознаки приймається.
Дата: 2019-02-02, просмотров: 1032.
